数学高中苏教版必修一《指数函数》(第1课时)课件
文档属性
| 名称 | 数学高中苏教版必修一《指数函数》(第1课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 280.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-12 15:07:26 | ||
图片预览








文档简介
课件31张PPT。2.2.2 指数函数
?第一课时学习目标
1.理解指数函数的概念,掌握指数函数的性质.
2.会求与指数函数有关的函数的定义域、值域. 课堂互动讲练知能优化训练课前自主学案第一课时课前自主学案1.对于幂an,
(1)当a>0,且a≠1时,使an有意义的n的范围是_____;
(2)当a=1时,an=_______.
2.如果y=f(x)在D上是增函数,则对任意x1,x2∈D且x1<x2,有f(x1)_____ f(x2)(填“>”或“<”或“=”),y=f(x)的图象从左至右逐渐_______ (填“上升”或“下降”).1<上升RR1.指数函数的定义
函数y=ax(a>0,且a≠1)叫做指数函数,x为自变量,定义域为______.
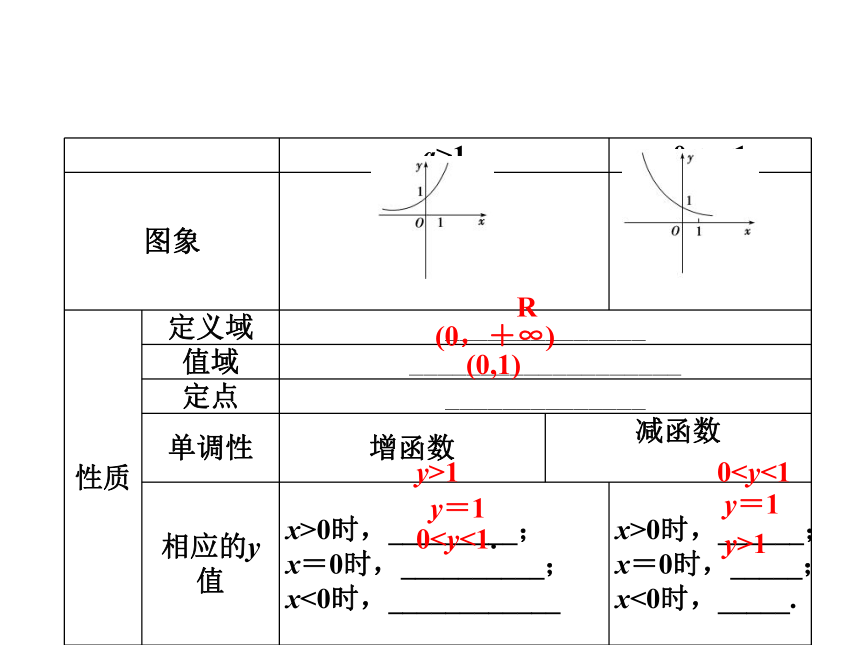
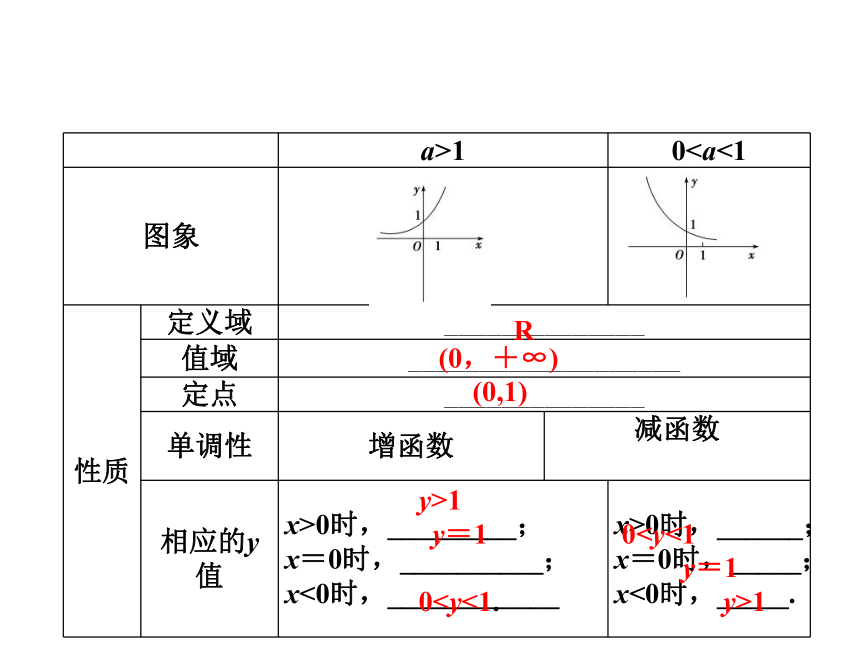
2.指数函数的图象与性质
(0,+∞)(0,1)y>1y=101R(0,+∞)(0,1)y>1y=101R(0,+∞)(0,1)y>1y=101R函数y=kax(k≠a,a>0,且a≠1),y=ax+1是指数函数吗?
提示:不是.形如y=ax(a>0且a≠1)的函数才是指数函数.课堂互动讲练指数函数的概念指数函数是从函数表达式的结构特征定义的:①底数a是大于0且不等于1的常数;②ax中的x的位置仅为x;③ax前面的系数为1. 函数y=(a2-3a+3)ax是指数函数,求a的值.解:根据指数函数的定义,指数函数满足:①前面系数为1;②底数a>0,且a≠1;③指数是自变量.
(1)y=πx,底数为π,满足π>0,且π≠1,前面系数为1,且指数为自变量x,故它是指数函数;
(2)y=(-4)x,底数-4<0,故它不是指数函数;
(3)y=-4x,前面系数为-1,故它不是指数函
数;
(4)y=x4,指数为4而不是x,故它不是指数函数;
对于形如f(x)=ag(x)的函数求定义域时,就是求使得g(x)有意义的x的取值集合;求值域时,需考虑函数y=ax的单调性,同时注意g(x)的取值范围.指数函数的定义域与值域 求下列函数的定义域和值域.【名师点评】 对于函数y=af(x)的定义域:使f(x)有意义的x的取值范围,值域:(1)根据定义域求出μ=f(x)的值域,(2)根据指数函数的性质求出y=aμ的值域,即为所求.
比较大小问题对于给出的数值,首先应判断转化为哪类函数,然后利用函数的单调性解决;若不能看作同一函数的两个值,常借助于中间量来过渡,中间量常用0和1. (本题满分14分)比较下列各组数的大小.
(1)1.8-π,1.8-3;(2)1.7-0.3,1.9-0.3;
(3)0.80.6,0.60.8.【名师点评】 对于同底数幂,应利用指数函数的单调性求解;对于同指数的两个函数值,应根据“在y轴的右侧,图象由上到下,底数越来越小”来判断数值的大小;对于不同底数,不同指数的两个函数值,可找一中间函数值,通过“搭桥”来达到比较两个数的大小的目的.自我挑战2 如果a-5x>ax+7(a>0,且a≠1),求x的取值范围.1.比较两个指数式的大小时应注意:
(1)对于底数相同、指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断;
(2)对于底数不同、指数相同的两个幂的大小比较,可利用指数函数图象的变化规律来判断,或用比商法;
(3)对于底数不同,且指数也不同的幂的大小比较,则应通过中间值来比较;本部分内容讲解结束Thank you!
?第一课时学习目标
1.理解指数函数的概念,掌握指数函数的性质.
2.会求与指数函数有关的函数的定义域、值域. 课堂互动讲练知能优化训练课前自主学案第一课时课前自主学案1.对于幂an,
(1)当a>0,且a≠1时,使an有意义的n的范围是_____;
(2)当a=1时,an=_______.
2.如果y=f(x)在D上是增函数,则对任意x1,x2∈D且x1<x2,有f(x1)_____ f(x2)(填“>”或“<”或“=”),y=f(x)的图象从左至右逐渐_______ (填“上升”或“下降”).1<上升RR1.指数函数的定义
函数y=ax(a>0,且a≠1)叫做指数函数,x为自变量,定义域为______.
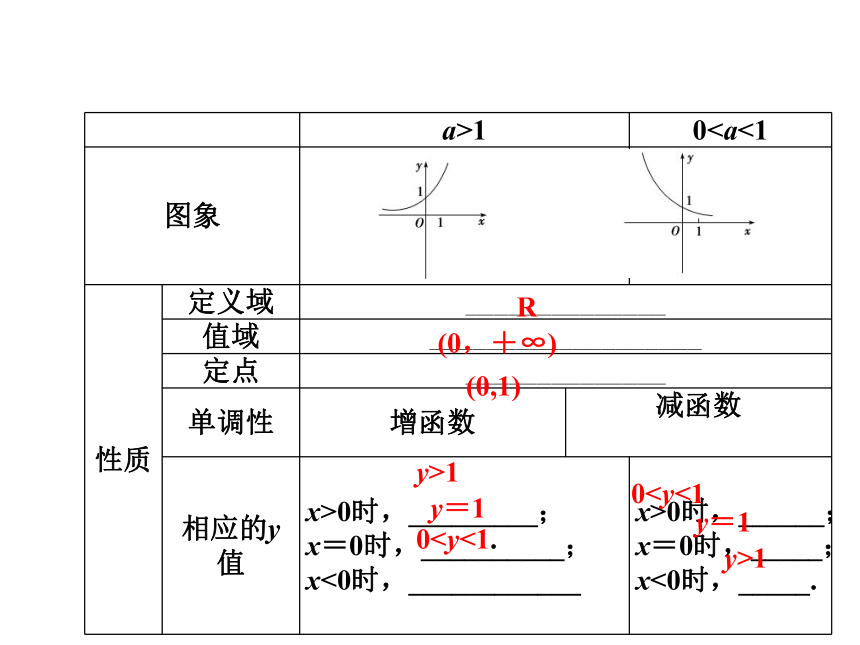
2.指数函数的图象与性质
(0,+∞)(0,1)y>1y=10
提示:不是.形如y=ax(a>0且a≠1)的函数才是指数函数.课堂互动讲练指数函数的概念指数函数是从函数表达式的结构特征定义的:①底数a是大于0且不等于1的常数;②ax中的x的位置仅为x;③ax前面的系数为1. 函数y=(a2-3a+3)ax是指数函数,求a的值.解:根据指数函数的定义,指数函数满足:①前面系数为1;②底数a>0,且a≠1;③指数是自变量.
(1)y=πx,底数为π,满足π>0,且π≠1,前面系数为1,且指数为自变量x,故它是指数函数;
(2)y=(-4)x,底数-4<0,故它不是指数函数;
(3)y=-4x,前面系数为-1,故它不是指数函
数;
(4)y=x4,指数为4而不是x,故它不是指数函数;
对于形如f(x)=ag(x)的函数求定义域时,就是求使得g(x)有意义的x的取值集合;求值域时,需考虑函数y=ax的单调性,同时注意g(x)的取值范围.指数函数的定义域与值域 求下列函数的定义域和值域.【名师点评】 对于函数y=af(x)的定义域:使f(x)有意义的x的取值范围,值域:(1)根据定义域求出μ=f(x)的值域,(2)根据指数函数的性质求出y=aμ的值域,即为所求.
比较大小问题对于给出的数值,首先应判断转化为哪类函数,然后利用函数的单调性解决;若不能看作同一函数的两个值,常借助于中间量来过渡,中间量常用0和1. (本题满分14分)比较下列各组数的大小.
(1)1.8-π,1.8-3;(2)1.7-0.3,1.9-0.3;
(3)0.80.6,0.60.8.【名师点评】 对于同底数幂,应利用指数函数的单调性求解;对于同指数的两个函数值,应根据“在y轴的右侧,图象由上到下,底数越来越小”来判断数值的大小;对于不同底数,不同指数的两个函数值,可找一中间函数值,通过“搭桥”来达到比较两个数的大小的目的.自我挑战2 如果a-5x>ax+7(a>0,且a≠1),求x的取值范围.1.比较两个指数式的大小时应注意:
(1)对于底数相同、指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断;
(2)对于底数不同、指数相同的两个幂的大小比较,可利用指数函数图象的变化规律来判断,或用比商法;
(3)对于底数不同,且指数也不同的幂的大小比较,则应通过中间值来比较;本部分内容讲解结束Thank you!
