数学高中苏教版必修一《指数函数》(第2课时)课件
文档属性
| 名称 | 数学高中苏教版必修一《指数函数》(第2课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 288.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-12 15:08:17 | ||
图片预览









文档简介
课件32张PPT。2.2.2 指数函数
?第二课时学习目标
1.会作与指数函数有关的函数图象.
2.掌握指数函数的单调性并会利用指数函数的单调性解决相关问题.
3.会用指数函数模型解决生活中的实际问题. 课堂互动讲练知能优化训练课前自主学案第二课时课前自主学案1.函数y=ax(a>0且a≠1)叫做________,其中x是自变量,函数定义域是R,值域是_________.
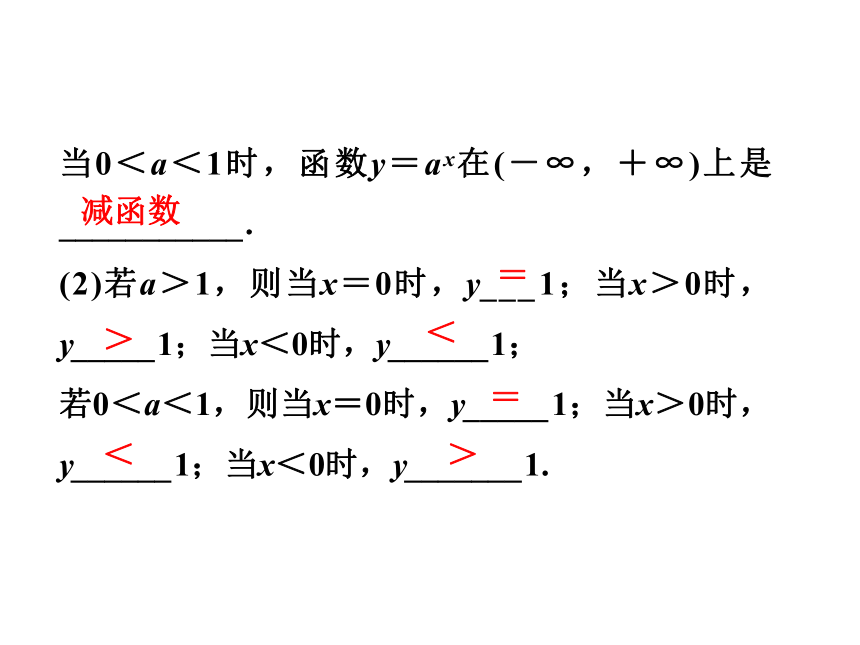
2.(1)当a>1时,函数y=ax在(-∞,+∞)上是_______________;指数函数(0,+∞)增函数当0<a<1时,函数y=ax在(-∞,+∞)上是___________.
(2)若a>1,则当x=0时,y___1;当x>0时,y_____1;当x<0时,y______1;
若0<a<1,则当x=0时,y_____1;当x>0时,y______1;当x<0时,y_______1.
减函数=><=<>|a|与作函数图象相关的几种常见的变换
(1)平移变换
①沿x轴:将y=f(x)的图象向左(a>0)或向右(a<0)平移______个单位以后,得到函数y=f(x+a),(a≠0)的图象.
②沿y轴:将y=f(x)的图象向上(b>0)或向下(b<0)平移_______个单位以后,得到函数y=f(x)+b,(b≠0)的图象.
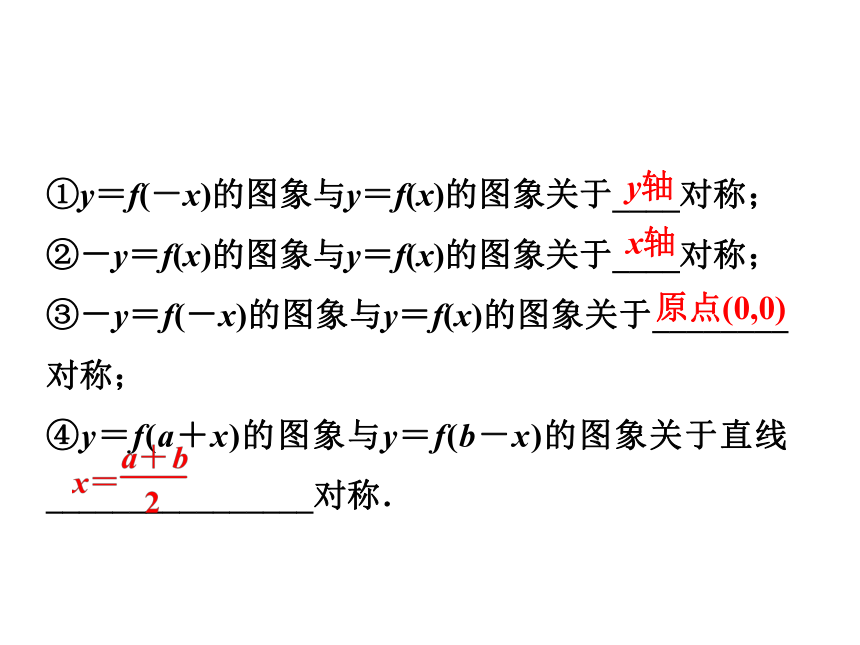
(2)对称变换|b|①y=f(-x)的图象与y=f(x)的图象关于____对称;
②-y=f(x)的图象与y=f(x)的图象关于____对称;
③-y=f(-x)的图象与y=f(x)的图象关于________对称;
④y=f(a+x)的图象与y=f(b-x)的图象关于直线________________对称.
y轴x轴原点(0,0)1.函数y=f(|x|)一定是偶函数吗?
提示:不一定,还应考虑该函数的定义域是否满足偶函数的条件.
2.函数y=3x-1的图象与x轴有一个交点,是否正确?
提示:不正确,把y=3x的图象向右平移一个单位得到y=3x-1的图象,图象位于x轴上方,与x轴无交点.课堂互动讲练函数图象的变换利用熟悉的函数图象作图,主要利用图象的平移、对称等变换,平移需分清楚向何方向平移,要移几个单位;对称需分清楚对称轴是什么,可以通过点与点的坐标关系来判断等.解:图象如图所示.函数的图象可反映出函数的有关性质,准确作出有关的图象,利用数形结合法可解决图象交点、方程根等一系列问题.函数图象的应用 根据函数y=|2x-1|的图象,判断当实数m为何值时,方程|2x-1|=m无解?有一解?有两解?
【思路点拨】 利用y=2x的图象,结合图象变换作y=|2x-1|的图象.函数y=m的图象是与x轴平行的直线,观察两图象的关系可知:
当m<0时,两函数图象没有公共点,此时方程|2x-1|=m无解;
当m=0或m≥1时,两函数图象只有一个公共点,此时方程|2x-1|=m有一解;
当0<m<1时,两函数图象有两个公共点,此时方程|2x-1|=m有两解.指数函数实际应用题在实际问题中,经常会遇到指数增长模型,设原有产值为N,平均增长率为P,则经过x年后,总产值y可以用y=N(1+P)x来表示,我们把形如y=kax(k∈R,a>0,且a≠1)的函数称为指数型函数,这是在实际生活中经常用到的数学模型. (本题满分14分)1981年,我国年人均收入为255美元,若到2001年人民生活达到小康水平,即年人均收入达到817美元,则年平均增长率是多少?若不低于此增长率递增,则到2011年年人均收入至少为多少美元?(精确到个位)
【思路点拨】 由题意,可知人均收入每年均呈指数型增长.【名师点评】 寻找合适的指数函数模型,要仔细从题目中找到条件,本题计算数字较大,要求精确数,这要求计算要精确.
自我挑战2 一个人喝了少量酒后,血液中酒精含量迅速上升到0.3 mg/mL,在停止喝酒后,血液中的酒精含量以每小时50%的速度减少.为了保障交通安全,某地交通规则规定,驾驶员血液酒精含量不得超过0.08 mg/mL,那么这名喝了少量酒的驾驶员,至少要过几小时才能驾驶(精确到小时)?
1.对于函数的图象,要注意以下几点:
(1)识图:由图象能得到函数的性质,这些性质主要指定义域、值域、奇偶性、单调性等.
(2)作图:作图的方法主要有两种:列表描点法和变换作图法.变换作图中要注意变换的顺序及变换的“作用点”.
(3)用图:用图为我们解决问题提供了很大的方便.数形结合的思想方法主要是用图,但要注意,此类问题有时需要转化,转化成函数问题,才可以作图象,从而才可以用图.2.图象变换
(1)对于左右平移变换,可以简单记作:左加右减.
(2)对于上下平移变换,可简单记作:上加下减.
(3)对于对称变换的特点:关于x轴对称:“y”变为“-y”;
关于y轴对称:“x”变为“-x”.可简单记作关于哪个轴对称,哪个轴对应的变量不变.本部分内容讲解结束Thank you!
?第二课时学习目标
1.会作与指数函数有关的函数图象.
2.掌握指数函数的单调性并会利用指数函数的单调性解决相关问题.
3.会用指数函数模型解决生活中的实际问题. 课堂互动讲练知能优化训练课前自主学案第二课时课前自主学案1.函数y=ax(a>0且a≠1)叫做________,其中x是自变量,函数定义域是R,值域是_________.
2.(1)当a>1时,函数y=ax在(-∞,+∞)上是_______________;指数函数(0,+∞)增函数当0<a<1时,函数y=ax在(-∞,+∞)上是___________.
(2)若a>1,则当x=0时,y___1;当x>0时,y_____1;当x<0时,y______1;
若0<a<1,则当x=0时,y_____1;当x>0时,y______1;当x<0时,y_______1.
减函数=><=<>|a|与作函数图象相关的几种常见的变换
(1)平移变换
①沿x轴:将y=f(x)的图象向左(a>0)或向右(a<0)平移______个单位以后,得到函数y=f(x+a),(a≠0)的图象.
②沿y轴:将y=f(x)的图象向上(b>0)或向下(b<0)平移_______个单位以后,得到函数y=f(x)+b,(b≠0)的图象.
(2)对称变换|b|①y=f(-x)的图象与y=f(x)的图象关于____对称;
②-y=f(x)的图象与y=f(x)的图象关于____对称;
③-y=f(-x)的图象与y=f(x)的图象关于________对称;
④y=f(a+x)的图象与y=f(b-x)的图象关于直线________________对称.
y轴x轴原点(0,0)1.函数y=f(|x|)一定是偶函数吗?
提示:不一定,还应考虑该函数的定义域是否满足偶函数的条件.
2.函数y=3x-1的图象与x轴有一个交点,是否正确?
提示:不正确,把y=3x的图象向右平移一个单位得到y=3x-1的图象,图象位于x轴上方,与x轴无交点.课堂互动讲练函数图象的变换利用熟悉的函数图象作图,主要利用图象的平移、对称等变换,平移需分清楚向何方向平移,要移几个单位;对称需分清楚对称轴是什么,可以通过点与点的坐标关系来判断等.解:图象如图所示.函数的图象可反映出函数的有关性质,准确作出有关的图象,利用数形结合法可解决图象交点、方程根等一系列问题.函数图象的应用 根据函数y=|2x-1|的图象,判断当实数m为何值时,方程|2x-1|=m无解?有一解?有两解?
【思路点拨】 利用y=2x的图象,结合图象变换作y=|2x-1|的图象.函数y=m的图象是与x轴平行的直线,观察两图象的关系可知:
当m<0时,两函数图象没有公共点,此时方程|2x-1|=m无解;
当m=0或m≥1时,两函数图象只有一个公共点,此时方程|2x-1|=m有一解;
当0<m<1时,两函数图象有两个公共点,此时方程|2x-1|=m有两解.指数函数实际应用题在实际问题中,经常会遇到指数增长模型,设原有产值为N,平均增长率为P,则经过x年后,总产值y可以用y=N(1+P)x来表示,我们把形如y=kax(k∈R,a>0,且a≠1)的函数称为指数型函数,这是在实际生活中经常用到的数学模型. (本题满分14分)1981年,我国年人均收入为255美元,若到2001年人民生活达到小康水平,即年人均收入达到817美元,则年平均增长率是多少?若不低于此增长率递增,则到2011年年人均收入至少为多少美元?(精确到个位)
【思路点拨】 由题意,可知人均收入每年均呈指数型增长.【名师点评】 寻找合适的指数函数模型,要仔细从题目中找到条件,本题计算数字较大,要求精确数,这要求计算要精确.
自我挑战2 一个人喝了少量酒后,血液中酒精含量迅速上升到0.3 mg/mL,在停止喝酒后,血液中的酒精含量以每小时50%的速度减少.为了保障交通安全,某地交通规则规定,驾驶员血液酒精含量不得超过0.08 mg/mL,那么这名喝了少量酒的驾驶员,至少要过几小时才能驾驶(精确到小时)?
1.对于函数的图象,要注意以下几点:
(1)识图:由图象能得到函数的性质,这些性质主要指定义域、值域、奇偶性、单调性等.
(2)作图:作图的方法主要有两种:列表描点法和变换作图法.变换作图中要注意变换的顺序及变换的“作用点”.
(3)用图:用图为我们解决问题提供了很大的方便.数形结合的思想方法主要是用图,但要注意,此类问题有时需要转化,转化成函数问题,才可以作图象,从而才可以用图.2.图象变换
(1)对于左右平移变换,可以简单记作:左加右减.
(2)对于上下平移变换,可简单记作:上加下减.
(3)对于对称变换的特点:关于x轴对称:“y”变为“-y”;
关于y轴对称:“x”变为“-x”.可简单记作关于哪个轴对称,哪个轴对应的变量不变.本部分内容讲解结束Thank you!
