数学高中苏教版必修一《函数的简单性质》课件1
文档属性
| 名称 | 数学高中苏教版必修一《函数的简单性质》课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 259.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-12 00:00:00 | ||
图片预览






文档简介
课件29张PPT。2.1.3 函数的简单性质
?第二课时学习目标
1.会利用函数的单调性求函数的最值.
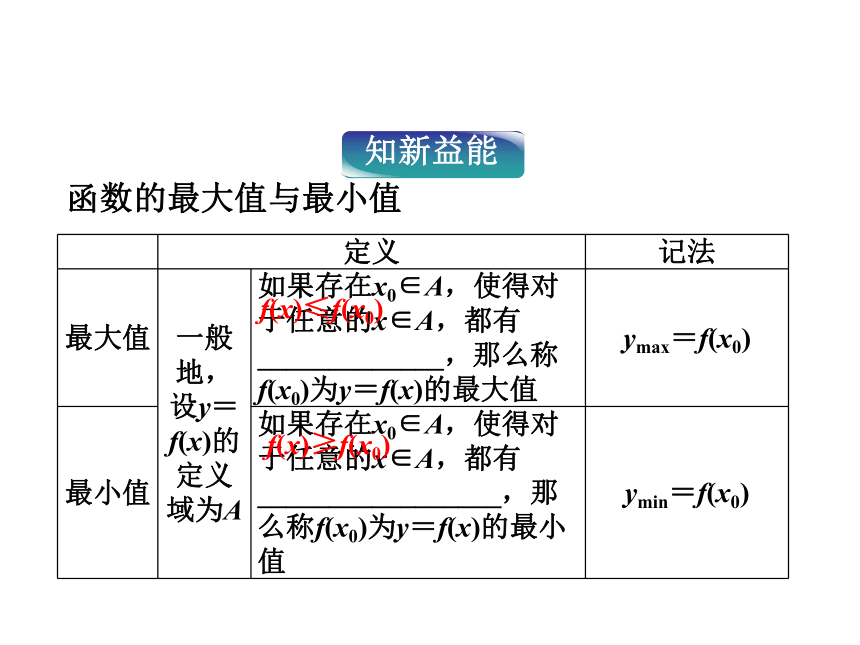
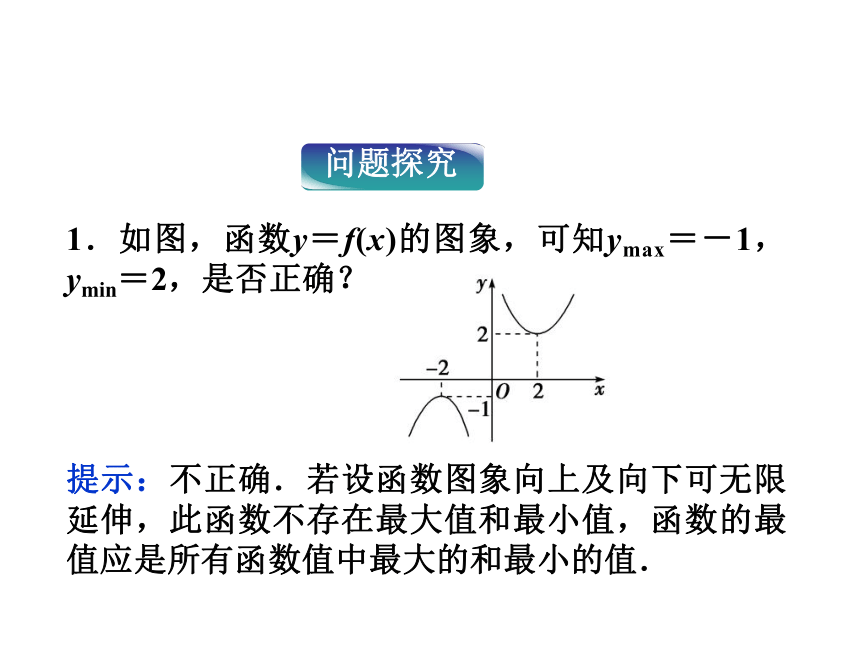
2.掌握几种常见的求函数最值的方法(如配方法、换元法、数形结合法)等. 课堂互动讲练知能优化训练课前自主学案第二课时课前自主学案从函数f(x)=x2的图象上还可看出,当x=0时,y=0是所有函数值中_______.而对于f(x)=-x2来说,x=0时,y=0是所有函数值中_______.最小的最大的函数的最大值与最小值f(x)≤f(x0)f(x)≥f(x0)1.如图,函数y=f(x)的图象,可知ymax=-1,ymin=2,是否正确?
提示:不正确.若设函数图象向上及向下可无限延伸,此函数不存在最大值和最小值,函数的最值应是所有函数值中最大的和最小的值.2.函数的最值与值域之间有什么关系?
提示:(1)函数的最值与函数的值域是不同的,函数的值域是一个集合,函数的最值属于这个集合.即f(x0)首先是一个函数值,它是值域的一个元素,而函数的最值是具体的一个函数值;
(2)函数的值域一定存在,但函数并不一定有最大(小)值.
课堂互动讲练利用单调性求函数的最值函数f(x)在[a,b]上单调递增时,f(x)max=f(b);函数f(x)在[a,b]上单调递减时,f(x)max=f(a);函数f(x)在[a,b]上不是单调函数时,找出图象上最高点的纵坐标,即为函数f(x)的最大值,图象上最低点的纵坐标,即为函数f(x)的最小值.【名师点评】 根据函数的单调性求最值
(值域)的步骤:
①求函数的定义域;
②证明函数在相应区间上的单调性;
③求出函数在定义域上的最值;
④写出值域.
二次函数是高中阶段研究的主要函数,求其最值问题有不含参数和含参数的二次函数求最值,对自变量x有限制和无限制两类情况,一般结合二次函数的图象来解答.二次函数的最值问题【思路点拨】 通过换元,转化为二次函数求最值问题. (本题满分14分)已知函数f(x)=x2+2ax+2,求f(x)在[-5,5]上的最大值.
【思路点拨】 由于二次函数的最值与对称轴有关,而本题中函数的对称轴为直线x=-a,位置不确定,所以应按对称轴与区间[-5,5]的相对位置进行分类讨论.
【名师点评】 二次函数在给定区间[m,n]上的最值求解常见的有以下三种情况:
①对称轴与区间[m,n]均是确定的;
②动轴定区间,即对称轴不确定,区间[m,n]是确定的;
③定轴动区间,即对称轴是确定的,区间[m,n]不确定.
以上三种情况,对于①可数形结合,较易解决;对于②和③,应按对称轴在区间的左侧、内部、右侧分三类结合其图象特征分别求解.
自我挑战2 当x∈[0,1]时,求函数f(x)=x2+(2-6a)x+3a2的最小值.本部分内容讲解结束Thank you!
?第二课时学习目标
1.会利用函数的单调性求函数的最值.
2.掌握几种常见的求函数最值的方法(如配方法、换元法、数形结合法)等. 课堂互动讲练知能优化训练课前自主学案第二课时课前自主学案从函数f(x)=x2的图象上还可看出,当x=0时,y=0是所有函数值中_______.而对于f(x)=-x2来说,x=0时,y=0是所有函数值中_______.最小的最大的函数的最大值与最小值f(x)≤f(x0)f(x)≥f(x0)1.如图,函数y=f(x)的图象,可知ymax=-1,ymin=2,是否正确?
提示:不正确.若设函数图象向上及向下可无限延伸,此函数不存在最大值和最小值,函数的最值应是所有函数值中最大的和最小的值.2.函数的最值与值域之间有什么关系?
提示:(1)函数的最值与函数的值域是不同的,函数的值域是一个集合,函数的最值属于这个集合.即f(x0)首先是一个函数值,它是值域的一个元素,而函数的最值是具体的一个函数值;
(2)函数的值域一定存在,但函数并不一定有最大(小)值.
课堂互动讲练利用单调性求函数的最值函数f(x)在[a,b]上单调递增时,f(x)max=f(b);函数f(x)在[a,b]上单调递减时,f(x)max=f(a);函数f(x)在[a,b]上不是单调函数时,找出图象上最高点的纵坐标,即为函数f(x)的最大值,图象上最低点的纵坐标,即为函数f(x)的最小值.【名师点评】 根据函数的单调性求最值
(值域)的步骤:
①求函数的定义域;
②证明函数在相应区间上的单调性;
③求出函数在定义域上的最值;
④写出值域.
二次函数是高中阶段研究的主要函数,求其最值问题有不含参数和含参数的二次函数求最值,对自变量x有限制和无限制两类情况,一般结合二次函数的图象来解答.二次函数的最值问题【思路点拨】 通过换元,转化为二次函数求最值问题. (本题满分14分)已知函数f(x)=x2+2ax+2,求f(x)在[-5,5]上的最大值.
【思路点拨】 由于二次函数的最值与对称轴有关,而本题中函数的对称轴为直线x=-a,位置不确定,所以应按对称轴与区间[-5,5]的相对位置进行分类讨论.
【名师点评】 二次函数在给定区间[m,n]上的最值求解常见的有以下三种情况:
①对称轴与区间[m,n]均是确定的;
②动轴定区间,即对称轴不确定,区间[m,n]是确定的;
③定轴动区间,即对称轴是确定的,区间[m,n]不确定.
以上三种情况,对于①可数形结合,较易解决;对于②和③,应按对称轴在区间的左侧、内部、右侧分三类结合其图象特征分别求解.
自我挑战2 当x∈[0,1]时,求函数f(x)=x2+(2-6a)x+3a2的最小值.本部分内容讲解结束Thank you!
