安徽省滁州市定远县吴圩片2021-2022学年九年级下学期期中考试数学试题(word版含答案)
文档属性
| 名称 | 安徽省滁州市定远县吴圩片2021-2022学年九年级下学期期中考试数学试题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 676.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-27 00:00:00 | ||
图片预览



文档简介
2021-2022学年九年级四月期中考试卷
数学试题
注意事项:
1.答题前,请将姓名、考生号、考点、考场号和座位号用黑色字迹的钢笔或签字笔填写在答题卡指定的位置上。
2.全卷共4页。考试时间:120分钟;满分:150分
3.作答单项选择题时,选出每题答案后,用2B铅笔把答题卡上对应题目的信息点框涂黑;如需改动,用橡皮擦干净后,再选涂其它答案。作答非选择题时,用黑色字迹的钢笔或签字笔将答案写在答题卡指定区域内。写在本试卷或草稿纸上,其答案一律无效。
4.考试结束后,请将答题卡交回。
第I卷(选择题 40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.-的相反数是( )
A.-2022 B.2022 C.±2022 D.
2.我省地处江、淮、汔沭泗流域下游和南北气候过渡带,滨江临海,河湖众多,地表水资源量达“亿”立方米,其中亿用科学记数法表示为( )
A. B. C. D.
3.如图,由5个完全相同的小正方体组合成的几何体,它的俯视图为( )
A. B. C. D.
4.下列计算正确的是( )
A. B.
C. D.
5.2012年张掖市政府投资2亿元人民币建设了廉租房8万平方米,预计2014年投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为( )
A.2(1+x)2=9.5 B.2(1+x)+2(1+x)2=9.5
C.2+2(1+x)+2(1+x)2=9.5 D.2(1+x)=9.5
6.估计的值在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间
7.若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1,x2,且x1≠x2,则m的取值范围是( )
A.m>﹣ B.m<﹣ C.m≥﹣ D.m≤﹣
8.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是( )
A.5 B. C.10﹣ D.15﹣
9.已知二次函数y=x2+bx-4图象上A、B两点关于原点对称,若经过A点的反比例函数的解析式是y=,则该二次函数的对称轴是直线( )
A.x="1" B.x="2" C.x="-1" D.x=-2
10.如图所示,边长为2的正方形绕点逆时针旋转后得到正方形,边与交于点,则四边形的周长( )
A. B. C. D.4
第II卷(非选择题110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.计算:_____.
12.把多项式因式分解的结果为______________.
13.如图,AB是半圆O的直径,AC=AD,∠CAB=20°,OE⊥CD,OE=,则半圆O的直径AB是_________
14.已知抛物线 (k为常数,且k≤3),当-1≤x≤3时,该抛物线对应的函数值有最大值-7,则k的值为______.
三、解答题(本大题共9小题,满分90分)
15.(每小题4分,满分8分)(1)计算:
(2)先化简,再求值:,其中.
16.(本大题满分6分)如图,在边长为1的正方形网格中,△ABO的顶点均在格点上,点A,B的坐标分别是A(2,2),B(1,3),把△ABO绕点O逆时针旋转90°后得到△A1B1O.
(1)画出△A1B1O,直接写出点A1,B1的坐标;
(2)求在旋转过程中,△ABO所扫过的面积.
17.(本大题满分12分)已知关于x、y的方程组中,x为非负数、y为负数.
(1)试求m的取值范围;
(2)当m取何整数时,不等式3mx+2x>3m+2的解集为x<1.
18.(本大题满分8分)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.
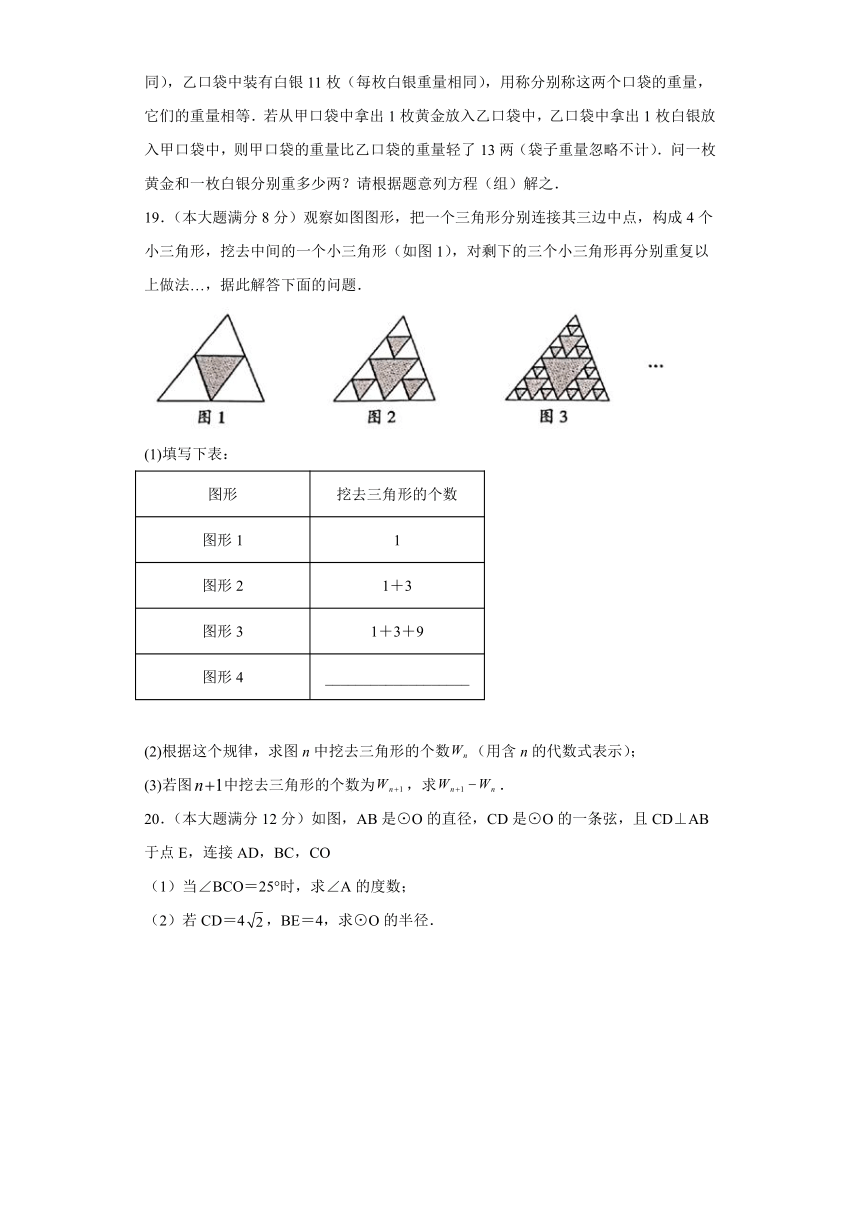
19.(本大题满分8分)观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法…,据此解答下面的问题.
(1)填写下表:
图形 挖去三角形的个数
图形1 1
图形2 1+3
图形3 1+3+9
图形4 ___________________
(2)根据这个规律,求图n中挖去三角形的个数(用含n的代数式表示);
(3)若图中挖去三角形的个数为,求.
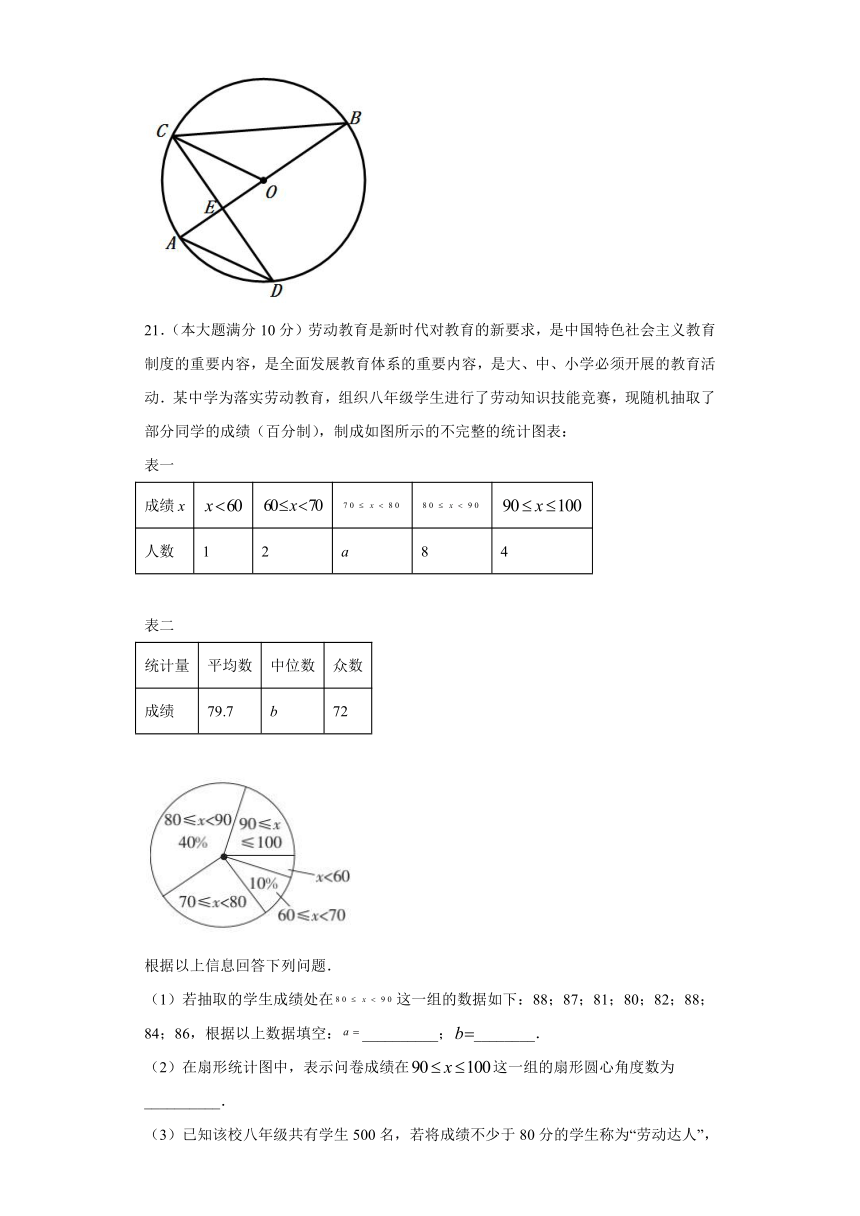
20.(本大题满分12分)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E,连接AD,BC,CO
(1)当∠BCO=25°时,求∠A的度数;
(2)若CD=4,BE=4,求⊙O的半径.
21.(本大题满分10分)劳动教育是新时代对教育的新要求,是中国特色社会主义教育制度的重要内容,是全面发展教育体系的重要内容,是大、中、小学必须开展的教育活动.某中学为落实劳动教育,组织八年级学生进行了劳动知识技能竞赛,现随机抽取了部分同学的成绩(百分制),制成如图所示的不完整的统计图表:
表一
成绩x
人数 1 2 a 8 4
表二
统计量 平均数 中位数 众数
成绩 79.7 b 72
根据以上信息回答下列问题.
(1)若抽取的学生成绩处在这一组的数据如下:88;87;81;80;82;88;84;86,根据以上数据填空:__________;________.
(2)在扇形统计图中,表示问卷成绩在这一组的扇形圆心角度数为__________.
(3)已知该校八年级共有学生500名,若将成绩不少于80分的学生称为“劳动达人”,请你估计该校八年级一共有多少名学生是“劳动达人”.
22.(本大题满分12分)如图,在平面直角坐标系中,直线分别交x轴、y轴于A,B两点,经过A,B两点的抛物线与x轴的正半轴相交于点.
(1)求抛物线的解析式;
(2)若P为线段AB上一点,,求AP的长;
(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
23.(本大题满分14分)如图,已知四边形是矩形,点在上,,与相交于点,且.
(1)连接,求证:;
(2)如图,连接并延长交于点,求的度数;
(3)若,求的长.
参考答案
1.D 2.C 3.D 4.B 5.A 6.C 7.A 8.D 9.C 10.B
11.
12.ab(a-3)2
13.4
14.或
15.(1)-3;(2)
解:(1)原式
;
(2)原式
.
当时,
原式.
16.(1)画出的△A1B1O见解析;A1(﹣2,2),B1(﹣3,1);(2)△ABO所扫过的面积为.
解:(1)由题意得:点位于第二象限,过点O作的垂线,在垂线上取一点使得,则点为点A的对应点;同样地方法,可以作出点,顺次连接即可得,结果如图所示:
由图可直接写成点的坐标为,点的坐标为;
(2)如图,根据旋转的过程可知,所扫过的面积等于扇形的面积与的面积之和
由坐标可知,
,即直角三角形
由题意可知,扇形的面积等于以O为圆心,以OB为半径的圆的面积的四分之一
则
故所扫过的面积为.
17.(1)
(2)x<1
(1)解:(1),
①+②得:2x=18﹣4m,x=9﹣2m,
①﹣②得:﹣2y=4+2m,y=﹣2﹣m,
∵x为非负数、y为负数,
∴,解得:﹣2(2)3mx+2x>3m+2,(3m+2)x>3m+2,
∵不等式3mx+2x>3m+2的解为x<1,
∴3m+2<0,
∴m<﹣,
由(1)得:﹣2∴﹣2∵m整数,
∴m=﹣1;
即当m=﹣1时,不等式3mx+2x>3m+2的解为x<1.
18.每枚黄金重两,每枚白银重两
解:设每枚黄金重x两,每枚白银重y两,
由题意得: ……①,
……②,
结合①②解得:,y,
答:每枚黄金重两,每枚白银重两.
19.(1)
(2)=
(3)
(1)解:图1挖去中间的1个小三角形,
图2挖去中间的(1+3)个小三角形,
图3挖去中间的(1+3+32)个小三角形,
则图4挖去中间的(1+3+32+33)个小三角形,即图4挖去中间的40个小三角形,
故答案为:1+3+32+33;
(2)解:由(1)知,图n中挖去三角形的个数wn=;答:wn=
(3)解:∵wn+1=,wn=
∴wn+1﹣wn
=()﹣()
=3n.
答:wn+1﹣wn=3n.
20.(1);(2)
解:(1)∵
∴
∵
∴
∵
∴在中,.
(2)∵是的直径,且于点
∴
∴在中,
∴设的半径为,则,
∴
∴
∴的半径为.
21.(1)5;81.5;(2);(3)300人
解:(1)根据抽取的60≤x<70为2人,在扇形中所占比例为10%,
所以,抽取总人数为2÷10%=20人.
因此a=20-1-2-8-4=5.
根据中位数定义,在所有抽取的的20人中,中位数是排名第10和第11两位同学成绩的平均数,因此只需找到排名第10和第11的两位同学即可.
根据图表一得知,排名第10和第11的两位同学在80≤x<90范围当中,80≤x<90范围之前已有8名同学,因此在80≤x<90范围中找寻排名第二和第三的即可.将80≤x<90这一组的数据进行从小到大排列,得到:80 81 82 84 86 87 88 88.因此第10名为81分,第11名为82分,因此中位数b=(81+82)÷2=81.5.
故答案为:5;81.5;
(2)这一范围共有4人,占抽取总人数的比例为4÷20=20%,
因此对应圆心角的度数为:360°×20%=72°.
故答案为:72°
(3)根据图表一,成绩在80分以上的同学共有8+4=12人,
占抽取总人数的比例为12÷20=60%,
因此该校八年级一共有500×60%=300名学生是“劳动达人”.
22.(1);(2);(3)存在,点N的坐标为(,3) 或(,)或(-4,-5)
解:(1)令,则,
∴点B的坐标为(0,3),
抛物线经过点B (0,3),C (1,0),
∴,解得,
∴抛物线的解析式为:;
(2)令,则,
解得:,
∴点A的坐标为(,0),
∴OA=3,OB=3,OC=1,
,
∵,且,
∴△PAO△CAB,
∴,即,
∴;
(3)存在,
过点P作PD⊥x轴于点D,
∵OA=3,OB=3,∠AOB=,
∴∠BAO=∠ABO=,
∴△PAD为等腰直角三角形,
∵,
∴PD=AD=2,
∴点P的坐标为(,2),
当N在AB的上方时,过点N作NE⊥y轴于点E,如图,
∵四边形APMN为平行四边形,
∴NM∥AP,NM=AP=,
∴∠NME=∠ABO=,
∴△NME为等腰直角三角形,
∴Rt△NMERt△APD,
∴NE=AD=2,
当时,,
∴点N的坐标为(,3),
当N在AB的下方时,过点N作NF⊥y轴于点F,如图,
同理可得:Rt△NMFRt△APD,
∴NF=AD=2,
当时,,
∴点N的坐标为(,),
当AP为平行四边形的对角线时,点N的横坐标为-4,
∴N(-4,-5),
综上,点N的坐标为(,3)、 (,)或(-4,-5) .
23.(1)证明:∵四边形是矩形,,
∴,
,
∴,
∴,
∵,
∴
(2)解:连接,
∵
∴,
∴,
∵,,
∴,
∴,
∴;
(3)解:∵四边形是矩形,
∴,,
∵,
∴,
∴,
∴,
设的长为,则,
∴,
解得,舍去,
∴的长为.
数学试题
注意事项:
1.答题前,请将姓名、考生号、考点、考场号和座位号用黑色字迹的钢笔或签字笔填写在答题卡指定的位置上。
2.全卷共4页。考试时间:120分钟;满分:150分
3.作答单项选择题时,选出每题答案后,用2B铅笔把答题卡上对应题目的信息点框涂黑;如需改动,用橡皮擦干净后,再选涂其它答案。作答非选择题时,用黑色字迹的钢笔或签字笔将答案写在答题卡指定区域内。写在本试卷或草稿纸上,其答案一律无效。
4.考试结束后,请将答题卡交回。
第I卷(选择题 40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.-的相反数是( )
A.-2022 B.2022 C.±2022 D.
2.我省地处江、淮、汔沭泗流域下游和南北气候过渡带,滨江临海,河湖众多,地表水资源量达“亿”立方米,其中亿用科学记数法表示为( )
A. B. C. D.
3.如图,由5个完全相同的小正方体组合成的几何体,它的俯视图为( )
A. B. C. D.
4.下列计算正确的是( )
A. B.
C. D.
5.2012年张掖市政府投资2亿元人民币建设了廉租房8万平方米,预计2014年投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为( )
A.2(1+x)2=9.5 B.2(1+x)+2(1+x)2=9.5
C.2+2(1+x)+2(1+x)2=9.5 D.2(1+x)=9.5
6.估计的值在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间
7.若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1,x2,且x1≠x2,则m的取值范围是( )
A.m>﹣ B.m<﹣ C.m≥﹣ D.m≤﹣
8.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是( )
A.5 B. C.10﹣ D.15﹣
9.已知二次函数y=x2+bx-4图象上A、B两点关于原点对称,若经过A点的反比例函数的解析式是y=,则该二次函数的对称轴是直线( )
A.x="1" B.x="2" C.x="-1" D.x=-2
10.如图所示,边长为2的正方形绕点逆时针旋转后得到正方形,边与交于点,则四边形的周长( )
A. B. C. D.4
第II卷(非选择题110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.计算:_____.
12.把多项式因式分解的结果为______________.
13.如图,AB是半圆O的直径,AC=AD,∠CAB=20°,OE⊥CD,OE=,则半圆O的直径AB是_________
14.已知抛物线 (k为常数,且k≤3),当-1≤x≤3时,该抛物线对应的函数值有最大值-7,则k的值为______.
三、解答题(本大题共9小题,满分90分)
15.(每小题4分,满分8分)(1)计算:
(2)先化简,再求值:,其中.
16.(本大题满分6分)如图,在边长为1的正方形网格中,△ABO的顶点均在格点上,点A,B的坐标分别是A(2,2),B(1,3),把△ABO绕点O逆时针旋转90°后得到△A1B1O.
(1)画出△A1B1O,直接写出点A1,B1的坐标;
(2)求在旋转过程中,△ABO所扫过的面积.
17.(本大题满分12分)已知关于x、y的方程组中,x为非负数、y为负数.
(1)试求m的取值范围;
(2)当m取何整数时,不等式3mx+2x>3m+2的解集为x<1.
18.(本大题满分8分)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.
19.(本大题满分8分)观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法…,据此解答下面的问题.
(1)填写下表:
图形 挖去三角形的个数
图形1 1
图形2 1+3
图形3 1+3+9
图形4 ___________________
(2)根据这个规律,求图n中挖去三角形的个数(用含n的代数式表示);
(3)若图中挖去三角形的个数为,求.
20.(本大题满分12分)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E,连接AD,BC,CO
(1)当∠BCO=25°时,求∠A的度数;
(2)若CD=4,BE=4,求⊙O的半径.
21.(本大题满分10分)劳动教育是新时代对教育的新要求,是中国特色社会主义教育制度的重要内容,是全面发展教育体系的重要内容,是大、中、小学必须开展的教育活动.某中学为落实劳动教育,组织八年级学生进行了劳动知识技能竞赛,现随机抽取了部分同学的成绩(百分制),制成如图所示的不完整的统计图表:
表一
成绩x
人数 1 2 a 8 4
表二
统计量 平均数 中位数 众数
成绩 79.7 b 72
根据以上信息回答下列问题.
(1)若抽取的学生成绩处在这一组的数据如下:88;87;81;80;82;88;84;86,根据以上数据填空:__________;________.
(2)在扇形统计图中,表示问卷成绩在这一组的扇形圆心角度数为__________.
(3)已知该校八年级共有学生500名,若将成绩不少于80分的学生称为“劳动达人”,请你估计该校八年级一共有多少名学生是“劳动达人”.
22.(本大题满分12分)如图,在平面直角坐标系中,直线分别交x轴、y轴于A,B两点,经过A,B两点的抛物线与x轴的正半轴相交于点.
(1)求抛物线的解析式;
(2)若P为线段AB上一点,,求AP的长;
(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
23.(本大题满分14分)如图,已知四边形是矩形,点在上,,与相交于点,且.
(1)连接,求证:;
(2)如图,连接并延长交于点,求的度数;
(3)若,求的长.
参考答案
1.D 2.C 3.D 4.B 5.A 6.C 7.A 8.D 9.C 10.B
11.
12.ab(a-3)2
13.4
14.或
15.(1)-3;(2)
解:(1)原式
;
(2)原式
.
当时,
原式.
16.(1)画出的△A1B1O见解析;A1(﹣2,2),B1(﹣3,1);(2)△ABO所扫过的面积为.
解:(1)由题意得:点位于第二象限,过点O作的垂线,在垂线上取一点使得,则点为点A的对应点;同样地方法,可以作出点,顺次连接即可得,结果如图所示:
由图可直接写成点的坐标为,点的坐标为;
(2)如图,根据旋转的过程可知,所扫过的面积等于扇形的面积与的面积之和
由坐标可知,
,即直角三角形
由题意可知,扇形的面积等于以O为圆心,以OB为半径的圆的面积的四分之一
则
故所扫过的面积为.
17.(1)
(2)x<1
(1)解:(1),
①+②得:2x=18﹣4m,x=9﹣2m,
①﹣②得:﹣2y=4+2m,y=﹣2﹣m,
∵x为非负数、y为负数,
∴,解得:﹣2
∵不等式3mx+2x>3m+2的解为x<1,
∴3m+2<0,
∴m<﹣,
由(1)得:﹣2
∴m=﹣1;
即当m=﹣1时,不等式3mx+2x>3m+2的解为x<1.
18.每枚黄金重两,每枚白银重两
解:设每枚黄金重x两,每枚白银重y两,
由题意得: ……①,
……②,
结合①②解得:,y,
答:每枚黄金重两,每枚白银重两.
19.(1)
(2)=
(3)
(1)解:图1挖去中间的1个小三角形,
图2挖去中间的(1+3)个小三角形,
图3挖去中间的(1+3+32)个小三角形,
则图4挖去中间的(1+3+32+33)个小三角形,即图4挖去中间的40个小三角形,
故答案为:1+3+32+33;
(2)解:由(1)知,图n中挖去三角形的个数wn=;答:wn=
(3)解:∵wn+1=,wn=
∴wn+1﹣wn
=()﹣()
=3n.
答:wn+1﹣wn=3n.
20.(1);(2)
解:(1)∵
∴
∵
∴
∵
∴在中,.
(2)∵是的直径,且于点
∴
∴在中,
∴设的半径为,则,
∴
∴
∴的半径为.
21.(1)5;81.5;(2);(3)300人
解:(1)根据抽取的60≤x<70为2人,在扇形中所占比例为10%,
所以,抽取总人数为2÷10%=20人.
因此a=20-1-2-8-4=5.
根据中位数定义,在所有抽取的的20人中,中位数是排名第10和第11两位同学成绩的平均数,因此只需找到排名第10和第11的两位同学即可.
根据图表一得知,排名第10和第11的两位同学在80≤x<90范围当中,80≤x<90范围之前已有8名同学,因此在80≤x<90范围中找寻排名第二和第三的即可.将80≤x<90这一组的数据进行从小到大排列,得到:80 81 82 84 86 87 88 88.因此第10名为81分,第11名为82分,因此中位数b=(81+82)÷2=81.5.
故答案为:5;81.5;
(2)这一范围共有4人,占抽取总人数的比例为4÷20=20%,
因此对应圆心角的度数为:360°×20%=72°.
故答案为:72°
(3)根据图表一,成绩在80分以上的同学共有8+4=12人,
占抽取总人数的比例为12÷20=60%,
因此该校八年级一共有500×60%=300名学生是“劳动达人”.
22.(1);(2);(3)存在,点N的坐标为(,3) 或(,)或(-4,-5)
解:(1)令,则,
∴点B的坐标为(0,3),
抛物线经过点B (0,3),C (1,0),
∴,解得,
∴抛物线的解析式为:;
(2)令,则,
解得:,
∴点A的坐标为(,0),
∴OA=3,OB=3,OC=1,
,
∵,且,
∴△PAO△CAB,
∴,即,
∴;
(3)存在,
过点P作PD⊥x轴于点D,
∵OA=3,OB=3,∠AOB=,
∴∠BAO=∠ABO=,
∴△PAD为等腰直角三角形,
∵,
∴PD=AD=2,
∴点P的坐标为(,2),
当N在AB的上方时,过点N作NE⊥y轴于点E,如图,
∵四边形APMN为平行四边形,
∴NM∥AP,NM=AP=,
∴∠NME=∠ABO=,
∴△NME为等腰直角三角形,
∴Rt△NMERt△APD,
∴NE=AD=2,
当时,,
∴点N的坐标为(,3),
当N在AB的下方时,过点N作NF⊥y轴于点F,如图,
同理可得:Rt△NMFRt△APD,
∴NF=AD=2,
当时,,
∴点N的坐标为(,),
当AP为平行四边形的对角线时,点N的横坐标为-4,
∴N(-4,-5),
综上,点N的坐标为(,3)、 (,)或(-4,-5) .
23.(1)证明:∵四边形是矩形,,
∴,
,
∴,
∴,
∵,
∴
(2)解:连接,
∵
∴,
∴,
∵,,
∴,
∴,
∴;
(3)解:∵四边形是矩形,
∴,,
∵,
∴,
∴,
∴,
设的长为,则,
∴,
解得,舍去,
∴的长为.
同课章节目录
