9.1反比例函数

课件29张PPT。第九章反比例函数 面积为200(m2)的矩形地块的长x(m)与宽y(m)之间有何关系?　　在小学里,我们已经知道,如果两个量x、y满足xy=k(k为常数,k≠0),那么x、y就成 ＿＿＿＿＿＿．反比例关系温故而知新 在一个变化的过程中有两个变量x和y，如果对于变量x的每一个值,变量y都有唯一的值与它对应,则y是x的函数.温故而知新什么是函数?速度v，时间t与路程s之间满足
（1）如果速度v一定时，路程s随与时间t成 关系.且对于时间t的每一个值，路程s都有 的一个值与它对应，它又是函数关系.因此，如果速度v一定时，路程s是时间t的 函数.
（2）如果时间t一定时，那么路程s与速度v又是什么关系呢？是函数关系吗？
答： ．
（3）如果路程s一定时，那么速度v和时间t又是什么关系呢？是函数关系吗？
答： ．
温故而知新正比例正比例S与v是正比例关系，是函数关系唯一v与t是反比例关系，是函数关系汽车从南京出发开往上海（全程约为300km），全程所用的时间t(h)随速度v(km/h)的变化而变化.
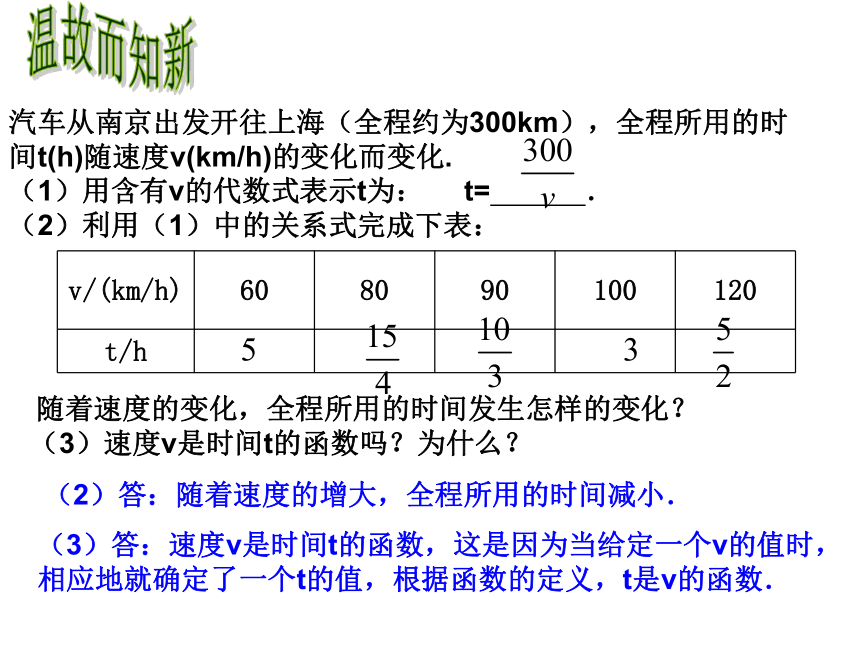
（1）用含有v的代数式表示t为： t= ．
（2）利用（1）中的关系式完成下表：温故而知新 随着速度的变化，全程所用的时间发生怎样的变化？
（3）速度v是时间t的函数吗？为什么？（2）答：随着速度的增大，全程所用的时间减小．（3）答：速度v是时间t的函数，这是因为当给定一个v的值时，相应地就确定了一个t的值，根据函数的定义，t是v的函数． 用函数关系式表示下列情景中的两个变量之间的关系：
（1）游泳池的容积为5000m3，向池内注水，注满水所需时间t(h)随注水速度v(m3/h)的变化而变化；
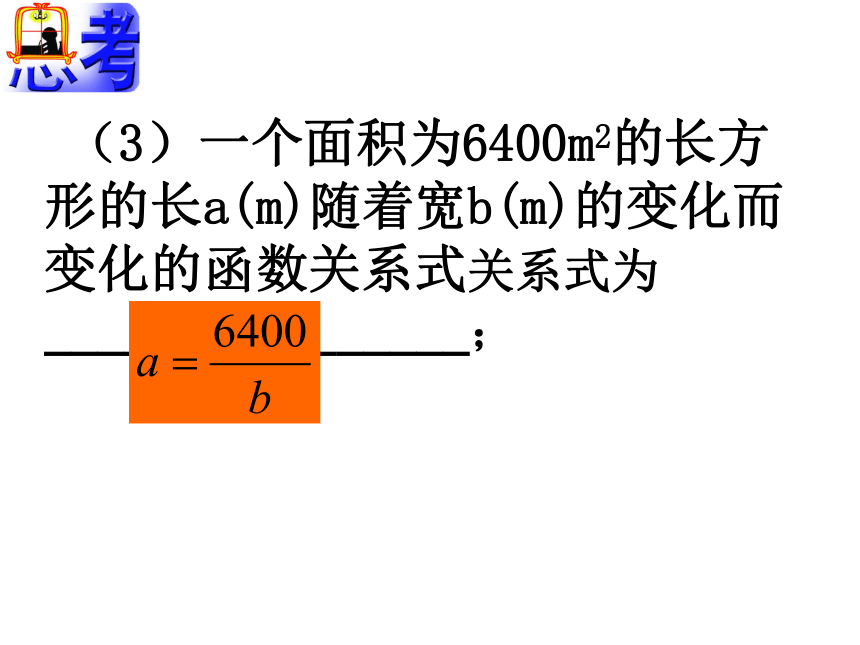
（2）用一块体积为300cm3的铁块制成钢丝，钢丝的横截面积S（cm2）随钢丝的长度L (cm)的变化而变化关系式为________________； （3）一个面积为6400m2的长方形的长a(m)随着宽b(m)的变化而变化的函数关系式关系式为________________； （4）某企业为资助贫困学生向教育部
门捐赠20万人民币，平均每位贫困学生获赠款额y（万元）随获赠学生的人数x（人）的变化而变化关系式为________________；

(5)实数m与n的积为－200，m随n的变化而变化关系式为________________．
反比例函数：形如
的函数叫做反比例函数，其中x是自变
量，y是x的函数，k是比例系数． 函数关系式
具有什么共同特征？
反比例函数的自变量x的取值范围是不等于0的一切实数．想一想（k为常数，且k≠0 ）
反比例函数的定义:比例系数一般的,形如 (k为常数,k ≠0) 的函数称为反比例函数.其中x是自变量,y是函数有时反比例函数也写成y=kx-1的形式.你还能举出类似的实例吗? 例1.下列关系式中的y是x的反比例函数吗?
如果是,比例系数k是多少?(1)y是x的反比例函数,比例系数k=4解: 例1.下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?y是x的反比例函数,比例系数k=解:可以改写成 (2)即 例1.下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?(3)y=1-x不具有解:(k为常数,k≠0)的形式,所以y不是x反比例函数 . 例1.下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?(4)xy=1可以改写成 ,所以y是x的反比例函数,比例系数k=1 .解: 例1.下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?(5) 不具有 (k为常数,k≠0)
的形式,所以y不是x反比例函数.解:例2 若函数 是反比例函数,求出m的值并写出函数关系式.分析: 因为函数
是反比例函数,所以x的
指数是－１,即
另外还要保证m-2≠0.解:由
得 m=±2
又∵m-2≠0, 即 m≠2
∴ m= - 2
∴函数关系式为
1、观察下面的表达式， y是否为x的反比例函数？若是，它们的 k 值分别是多少？(1) (2) (4) (3) (5)(6)√√√有时反比例函数也写成y=kx-1的形式.A组2、若 是反比例函数 ,求此反比例函数的关系式. 3、有一面积为60的梯形，其上底长是
下底长的 ，若下底长为x，高为
y，则y与x的函数关系式是 ,比例系数是________.4.对于函数y= ，当m 时，y是x的反比
例函数，比例系数是________.
5.菱形的面积为24cm ,两条对角线分别为xcm和
ycm,则y与x之间的函数关系式为_________,
比例系数为_________,当其中一条对角线x=6cm时,
另一条对角线y=__________.6.已知变量y与x成反比例，当x=3时，y=-6.
求：(1)y与x之间的函数关系式;
(2)当x=3 时，y的值.1、函数 ,
当m=_____时, 它是正比例函数,
当m=_____时,它是反比例函数. -3-1练 习 B组2.已知y-2与x成反比例,且当x=2时,y=4,求y与x之间的函数关系式.练 习 B组3.已知函数y = y1＋y2 ，y1与x成正比例，y2与x成反比例，且当x = 1时， y = 6,当x = 2时，y = 5,求y与x的函数关系式. 通过本节课的学习，你有什么收获？
还有什么困惑吗？及时小结，自我评价1.反比例函数定义.3.反比例函数是刻画现实的另一个数学模型．2.怎样判断一个函数是反比例函数?
不同点：
① x的位置不同（一个在分母上，一个在分子上）② x的取值不同，一个可以取任意值，一个除0以外的实数.③ 图象上存在差异.（以后学习了以比例函数的图象之后）.4.反比例函数与正比例函数的区别:相同点： ①只含有一个常数；
②求函数表达式时只要知道一对x、y的值；
③k≠0；比比看小测验作业:评价 P50-51 9.1课时 课本 P64 习题9.1 1、2、3