数学高中苏教版必修一2.5.2用二分法求方程的近似解
文档属性
| 名称 | 数学高中苏教版必修一2.5.2用二分法求方程的近似解 |

|
|
| 格式 | zip | ||
| 文件大小 | 231.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-12 00:00:00 | ||
图片预览




文档简介
课件13张PPT。§2.5.2 用二分法求方程的近似解2019年1月26日江苏省淮州中学 曾宁江§2.5.2 用二分法求方程的近似解问题情境:
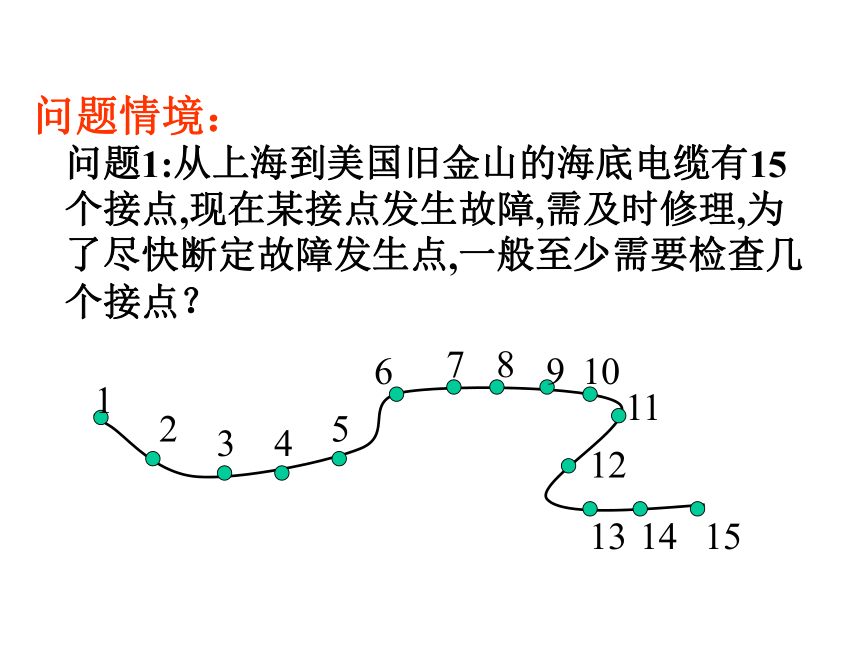
问题1:从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查几个接点?§2.5.2 用二分法求方程的近似解问题2
1.能否求解以下几个方程
(1) x2-2x-1=0
(2) 2x=4-x
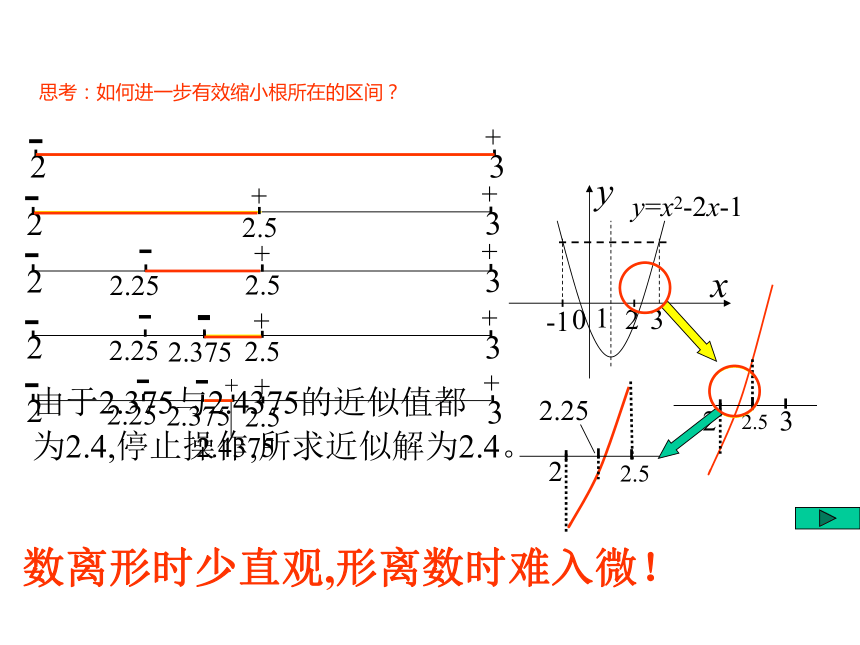
(3) x3+3x-1=02.不解方程,能否解出它们的近似解?指出:用配方法求得方程x2-2x-1=0的解,但此法不能运用于解另外两个方程。§2.5.2 用二分法求方程的近似解可得:方程x2-2x-1=0一个根x1在区间(2,3)内,另一个根x2在区间(-1,0)内例1 不解方程,如何求方程x2-2x-1=0的一个正的近似解(精确到0.1)? 由此可知:借助函数f(x)= x2-2x-1的图象,我们发现f(2)=-1<0,f(3)=2>0,这表明此函图象在区间(2,3)上穿过x轴一次,可得出方程在区间(2,3)上有惟一解.画出y=x2-2x-1的图象,如图§2.5.2 用二分法求方程的近似解思考:如何进一步有效缩小根所在的区间?数离形时少直观,形离数时难入微!由于2.375与2.4375的近似值都
为2.4,停止操作,所求近似解为2.4。§2.5.2 用二分法求方程的近似解1.简述上述求方程近似解的过程∵f(2.5)=0.25>0∵ f(2.25)=-0.4375<0∵ f(2.375)=- 0.2351<0∵ f(2.4375)= 0.105>0∵ 2.375与2.4375的近似值都是2.4, ∴x1≈2.4解:设f (x)=x2-2x-1,设x1为其正的零点§2.5.2 用二分法求方程的近似解2.二分法定义⑴自行探究定义 对于在区间[a,b]上连续不断,且f (a)f (b)<0的函数y=f (x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两端点逐步逼近零点,进而得到零点(或对应方程的根)近似解的方法叫做二分法。1、函数y=f (x)在[a,b]上连续不断。2、 y=f (x)满足 f (a)f (b)<0注意:§2.5.2 用二分法求方程的近似解 二分法求解方程f(x)=0(或g(x)=h(x))近似解的基本步骤:困难在哪里?确定第一个区间!(2)函数状态法;2.不断将解所在的区间一分为二;3.根据精确度得出近似解。?1.寻找解所在的区间:
(1)图象法;§2.5.2 用二分法求方程的近似解例2:利用计算器,求方程2x=4-x的近似解(精确到0.1)怎样找到它的解所在的区间呢?在同一坐标系内画函数y=2x
与y=4-x的图象,如图:提问:能否不画图确定根所在的区间?得:方程有一个解x0 ∈(0,4)如果画得很准确,可得x0 ∈(1,2)§2.5.2 用二分法求方程的近似解解:设函数f (x)=2x+x-4则f (x)在R上是增函数∵f (0)=-3<0, f (2)=2>0 ∴ f (x)在(0,2)内有惟一零点,
∴方程2x+x-4 =0在(0,2)内有惟一解x0。由f (1)=-1<0, f (2)=2>0得:x0∈(1,2)由f (1.5)=0.33>0, f (1)=-1<0得:x0∈(1,1.5)由f (1.25)=-0.37<0, f (1.5)>0得:x0∈(1.25,1.5)由f (1.375)=-0.031<0, f (1.5)>0得:x0∈(1.375,1.5)由f (1.4375)= 0.146>0, f (1.375)<0得:x0∈(1.375,1.4375)∵ 1.375与1.4375的近似值都是1.4, ∴x0≈1.4§2.5.2 用二分法求方程的近似解练习:求方程x3+3x-1=0的一个近似解
(精确到0.01)。画y=x3+3x-1的图象比较困难,变形为x3=1-3x,画两个函数的图象如何?有惟一解x0∈(0,1)§2.5.2 用二分法求方程的近似解回顾小结:本课学习了
1.二分法的解题思想,知道了二分法是一种求一元方程近似解的通法;
2.了解了二分法的解题步骤,会用二分法求某些一元方程的近似解.作业:P81 习题2.5 3 5⑴
2.预习课本P82~84 §2.6函数模型及应用
预习题:认真阅读本节的三个例题,理解其解法.Thanks 谢谢您的观看!
问题1:从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查几个接点?§2.5.2 用二分法求方程的近似解问题2
1.能否求解以下几个方程
(1) x2-2x-1=0
(2) 2x=4-x
(3) x3+3x-1=02.不解方程,能否解出它们的近似解?指出:用配方法求得方程x2-2x-1=0的解,但此法不能运用于解另外两个方程。§2.5.2 用二分法求方程的近似解可得:方程x2-2x-1=0一个根x1在区间(2,3)内,另一个根x2在区间(-1,0)内例1 不解方程,如何求方程x2-2x-1=0的一个正的近似解(精确到0.1)? 由此可知:借助函数f(x)= x2-2x-1的图象,我们发现f(2)=-1<0,f(3)=2>0,这表明此函图象在区间(2,3)上穿过x轴一次,可得出方程在区间(2,3)上有惟一解.画出y=x2-2x-1的图象,如图§2.5.2 用二分法求方程的近似解思考:如何进一步有效缩小根所在的区间?数离形时少直观,形离数时难入微!由于2.375与2.4375的近似值都
为2.4,停止操作,所求近似解为2.4。§2.5.2 用二分法求方程的近似解1.简述上述求方程近似解的过程∵f(2.5)=0.25>0∵ f(2.25)=-0.4375<0∵ f(2.375)=- 0.2351<0∵ f(2.4375)= 0.105>0∵ 2.375与2.4375的近似值都是2.4, ∴x1≈2.4解:设f (x)=x2-2x-1,设x1为其正的零点§2.5.2 用二分法求方程的近似解2.二分法定义⑴自行探究定义 对于在区间[a,b]上连续不断,且f (a)f (b)<0的函数y=f (x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两端点逐步逼近零点,进而得到零点(或对应方程的根)近似解的方法叫做二分法。1、函数y=f (x)在[a,b]上连续不断。2、 y=f (x)满足 f (a)f (b)<0注意:§2.5.2 用二分法求方程的近似解 二分法求解方程f(x)=0(或g(x)=h(x))近似解的基本步骤:困难在哪里?确定第一个区间!(2)函数状态法;2.不断将解所在的区间一分为二;3.根据精确度得出近似解。?1.寻找解所在的区间:
(1)图象法;§2.5.2 用二分法求方程的近似解例2:利用计算器,求方程2x=4-x的近似解(精确到0.1)怎样找到它的解所在的区间呢?在同一坐标系内画函数y=2x
与y=4-x的图象,如图:提问:能否不画图确定根所在的区间?得:方程有一个解x0 ∈(0,4)如果画得很准确,可得x0 ∈(1,2)§2.5.2 用二分法求方程的近似解解:设函数f (x)=2x+x-4则f (x)在R上是增函数∵f (0)=-3<0, f (2)=2>0 ∴ f (x)在(0,2)内有惟一零点,
∴方程2x+x-4 =0在(0,2)内有惟一解x0。由f (1)=-1<0, f (2)=2>0得:x0∈(1,2)由f (1.5)=0.33>0, f (1)=-1<0得:x0∈(1,1.5)由f (1.25)=-0.37<0, f (1.5)>0得:x0∈(1.25,1.5)由f (1.375)=-0.031<0, f (1.5)>0得:x0∈(1.375,1.5)由f (1.4375)= 0.146>0, f (1.375)<0得:x0∈(1.375,1.4375)∵ 1.375与1.4375的近似值都是1.4, ∴x0≈1.4§2.5.2 用二分法求方程的近似解练习:求方程x3+3x-1=0的一个近似解
(精确到0.01)。画y=x3+3x-1的图象比较困难,变形为x3=1-3x,画两个函数的图象如何?有惟一解x0∈(0,1)§2.5.2 用二分法求方程的近似解回顾小结:本课学习了
1.二分法的解题思想,知道了二分法是一种求一元方程近似解的通法;
2.了解了二分法的解题步骤,会用二分法求某些一元方程的近似解.作业:P81 习题2.5 3 5⑴
2.预习课本P82~84 §2.6函数模型及应用
预习题:认真阅读本节的三个例题,理解其解法.Thanks 谢谢您的观看!
