数学高中苏教版必修一《分数指数幂》
图片预览




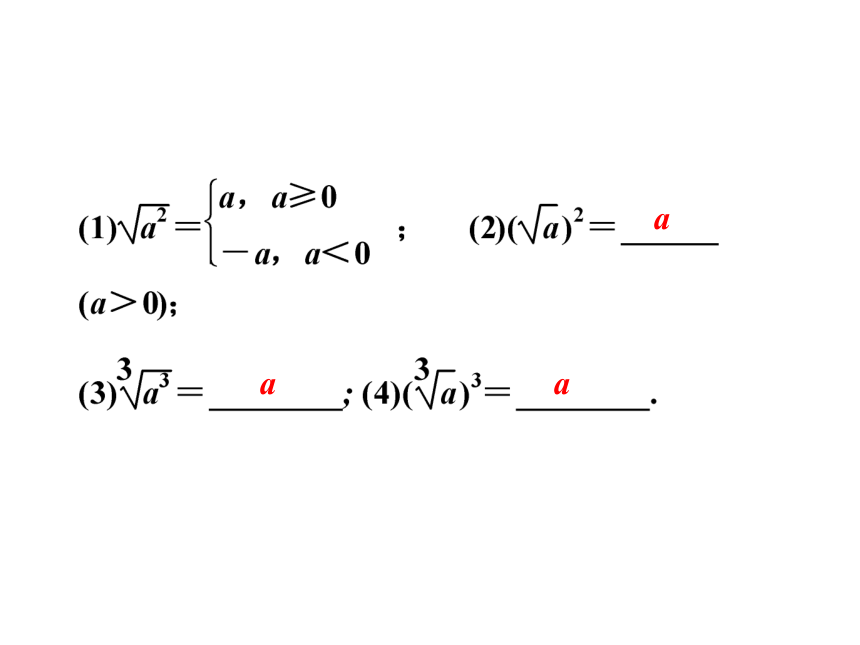






文档简介
课件32张PPT。2.2 指数函数
?2.2.1 分数指数幂学习目标
1.通过具体实例(如细胞的分裂,考古中所用的14C的衰减,药物在人体内残留量的变化等),了解指数函数模型的实际背景.
2.理解有理指数幂的含义,通过具体实例了解实数指数幂的意义,掌握幂的运算. 课堂互动讲练知能优化训练课前自主学案分数指数幂2.2.1课前自主学案1.在初中学过正整数指数幂:将
用_______表示,这里的n为正整数.
anam+nam-namnambm平方根立方根aaa0aa|a|(3)0的正分数指数幂等于0;
0的负分数指数幂无意义.
4.有理指数幂的运算性质
(1)asat=_______;
(2)(as)t=_____;
(3)(ab)t=______.
其中s,t∈Q,a>0,b>0.
as+tastatbt课堂互动讲练根式的化简求值根式的化简求值问题就是将根式化成分数指数幂的形式,然后利用分数指数幂的运算性质求解.对化简求值的结果,一般用分数指数幂的形式保留;在进行指数幂运算时,通常是化负指数为正指数,化根式为分数指数幂,化小数为分数,同时要兼顾运算的顺序.指数从整数扩充到有理数后,其运算性质am·an=am+n,(am)n=amn,(ab)n=anbn(a>0)也同样成立.分数指数幂是根式的又一种表现形式,利用分数指数进行根式运算,其顺序是先把根式化为分数指数幂,再根据幂的运算性质进行计算.分数指数幂的运算计算或化简:【名师点评】 (1)当化简的式子中既有根式又有分数指数幂时,一般先把根式统一为分数指数幂再化简.
(2)当所求根式含有多重根号时,要搞清被开方数,由里向外用分数指数幂写出,然后再运用性质进行化简.
(3)注意运算过程中不能随意扩大或缩小底数的范围.自我挑战2 计算或化简:
分数指数幂运算的条件求值对于条件求值问题,可以把所要求的式子先进行变形,寻找出与条件等式的联系,然后求值,也可以先对条件等式加以变形,使它与所要求的式子的联系更加明显,而后求值,运算的关键就是整体利用. (本题满分14分) 已知 ,求下列各式的值.
【思路点拨】 由题中所给的等式,容易想到用解方程的方法求出a的值,再分别代入各小题中进行求解,此种方法比【名师点评】 对于本类问题设而不求,整体代换是化简求值的一大捷径.1.关于根式的记忆口诀:
正数开方要分清,根指奇偶大不同,
根指为奇根一个,根指为偶双胞生.
负数只有奇次根,算术方根零或正,
正数若求偶次根,符号相反值相同.
负数开方要慎重,根指为奇才可行,
根指为偶无意义,零取方根仍为零.本部分内容讲解结束Thank you!
?2.2.1 分数指数幂学习目标
1.通过具体实例(如细胞的分裂,考古中所用的14C的衰减,药物在人体内残留量的变化等),了解指数函数模型的实际背景.
2.理解有理指数幂的含义,通过具体实例了解实数指数幂的意义,掌握幂的运算. 课堂互动讲练知能优化训练课前自主学案分数指数幂2.2.1课前自主学案1.在初中学过正整数指数幂:将
用_______表示,这里的n为正整数.
anam+nam-namnambm平方根立方根aaa0aa|a|(3)0的正分数指数幂等于0;
0的负分数指数幂无意义.
4.有理指数幂的运算性质
(1)asat=_______;
(2)(as)t=_____;
(3)(ab)t=______.
其中s,t∈Q,a>0,b>0.
as+tastatbt课堂互动讲练根式的化简求值根式的化简求值问题就是将根式化成分数指数幂的形式,然后利用分数指数幂的运算性质求解.对化简求值的结果,一般用分数指数幂的形式保留;在进行指数幂运算时,通常是化负指数为正指数,化根式为分数指数幂,化小数为分数,同时要兼顾运算的顺序.指数从整数扩充到有理数后,其运算性质am·an=am+n,(am)n=amn,(ab)n=anbn(a>0)也同样成立.分数指数幂是根式的又一种表现形式,利用分数指数进行根式运算,其顺序是先把根式化为分数指数幂,再根据幂的运算性质进行计算.分数指数幂的运算计算或化简:【名师点评】 (1)当化简的式子中既有根式又有分数指数幂时,一般先把根式统一为分数指数幂再化简.
(2)当所求根式含有多重根号时,要搞清被开方数,由里向外用分数指数幂写出,然后再运用性质进行化简.
(3)注意运算过程中不能随意扩大或缩小底数的范围.自我挑战2 计算或化简:
分数指数幂运算的条件求值对于条件求值问题,可以把所要求的式子先进行变形,寻找出与条件等式的联系,然后求值,也可以先对条件等式加以变形,使它与所要求的式子的联系更加明显,而后求值,运算的关键就是整体利用. (本题满分14分) 已知 ,求下列各式的值.
【思路点拨】 由题中所给的等式,容易想到用解方程的方法求出a的值,再分别代入各小题中进行求解,此种方法比【名师点评】 对于本类问题设而不求,整体代换是化简求值的一大捷径.1.关于根式的记忆口诀:
正数开方要分清,根指奇偶大不同,
根指为奇根一个,根指为偶双胞生.
负数只有奇次根,算术方根零或正,
正数若求偶次根,符号相反值相同.
负数开方要慎重,根指为奇才可行,
根指为偶无意义,零取方根仍为零.本部分内容讲解结束Thank you!
