数学高中苏教版必修一《函数》章末复习课件
文档属性
| 名称 | 数学高中苏教版必修一《函数》章末复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 336.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-12 20:15:35 | ||
图片预览










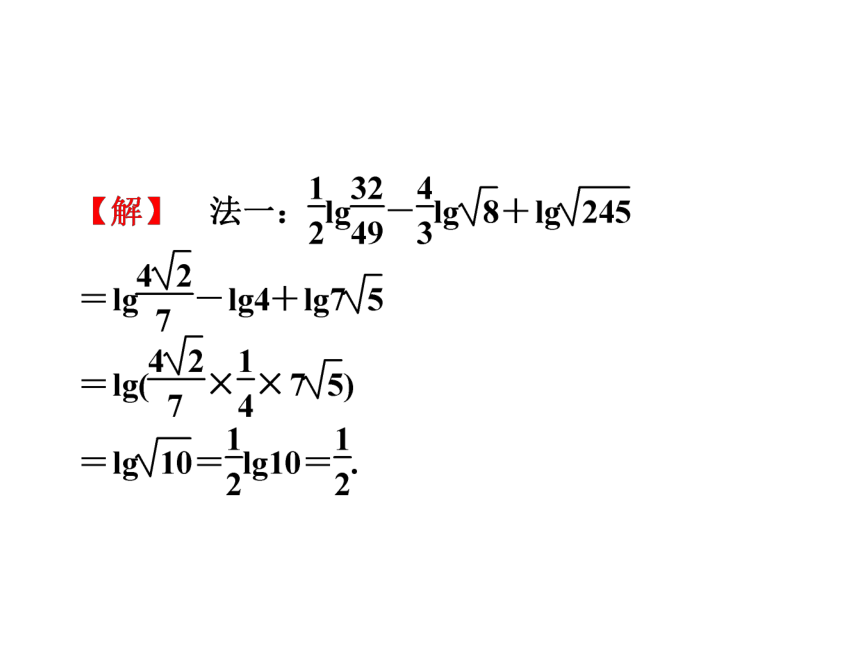
文档简介
课件41张PPT。本章优化总结 专题探究精讲章末综合检测本章优化总结知识体系网络知识体系网络专题探究精讲函数的三要素直接考查函数的定义域、值域、函数的解析式、求值等问题,解决这类问题需要清晰理解概念,掌握基本方法.【名师点评】 利用定义域的概念把问题转化为“恒成立”的题型,紧紧抓住一元二次不等式的解集,一元二次方程的根以及二次函数之间的关系,同时要正确理解值域的概念并能有效利用.有关指数、对数的运算问题指数与指数运算、对数与对数运算是两个重要的知识点,不仅是本章考查的重要问题类型,也是高考的必考内容.
指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为指数运算,其次若出现分式则要注意分子、分母因式分解以达到约分的目的,对数运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.【思路点拨】 利用幂指数及对数的运算性质.
【名师点评】 对幂值的计算,一般应尽可能把幂化为底数是质数的指数幂,再考虑同底数幂的运算法则及乘法公式.
对数运算中常常会逆用对数法则以达到化简的目的.对于不同底数的对数可以首先化为同底数的对数.函数的性质函数的单调性、奇偶性、最值问题是高考必考内容,通常综合考查函数的多个性质.②当-1<x1<x2<0时,x1-x2<0,0<x1x2<1,
∴x1x2-1<0.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
所以函数f(x)在(-1,0)上是减函数.
【名师点评】 (1)函数的奇偶性与单调性是函数的两个重要性质,解答问题时,要善于应用函数的观点,挖掘函数的奇偶性和单调性,并注意两者的联系.
(2)函数的单调性、奇偶性常与其他性质结合在一起进行考查,此类考查形式是常考点,应引起足够的重视.函数图象问题函数的图象是函数的重要表示方法.它具有直观性,通过函数图象能够掌握函数的重要性质.
利用数形结合解题有直观、明了、易懂的优点,在历届高考试题中,常出现有关函数图象和利用图象解题的试题.
所谓图象变换,就是把基本初等函数图象,通过平移、对称、翻折、伸缩等变换,变成复合函数的图象,因此要熟记基本函数图象,掌握变换的技巧方法. 已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数f2(x)的图象与直线y=x的两个交点间距离为8,f(x)=f1(x)+f2(x).
(1)求函数f(x)的表达式;
(2)求证:当a>3时,关于x的方程f(x)=f(a)有三个实数解.
【思路点拨】 本题从研究图象入手,直观地分析根的个数.构造基本初等函数是解题关键.【名师点评】 (1)熟记一次函数、二次函数、反比例函数、正比例函数、指数函数、对数函数的大致图象(关键点要准确).
(2)要有数形结合的意识“有数无形少直观,有形无数难入微”.函数的零点与方程的根的关系及应用根据函数零点的定义,函数y=f(x)的零点就是方程f(x)=0的根,判断一个函数是否有零点,有几个零点,就是判断方程f(x)=0是否有实根,有几个实根.从图象上说,函数的零点就是函数y=f(x)的图象与x轴的交点的横坐标.函数的零点、方程的根、函数图象与x轴的交点三者之间有着内在的本质联系,利用它们之间的关系,可以解决很多函数、方程与不等式的问题.在高考中有许多问题涉及三者的相互转化,思考时要多加注意.【名师点评】 求函数的零点或方程的根常用的方法有:
①直接法,即求f(x)=0的根;
②讨论函数y=f(x)的性质,画出它的图象,从而判定它与x轴的交点个数,就可以判定根的个数;
③利用根的存在性定理;
④函数与方程的思想应用,把方程转化成两个函数图象的交点问题.函数建模数学应用题是指带有一定生产、生活背景的数量化问题.解答数学应用题就是在阅读材料、理解题意的基础上,把实际问题转化为数学问题,建立相应的数学模型,再利用数学知识对模型进行分析、研究、解答,然后再把答案返回到实际问题中去,获取具有实际意义的结论.其基本程序如下: 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上;该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如下表所示:(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y表示该股票日交易额(万元),写出y关于t的函数关系式,并求在这30天中第几天日交易额最大,最大值是多少?
【思路点拨】 由图象和表格可直接写出函数关系式,由(1)(2)问的函数关系式相乘,可得第(3)问的函数关系式,再求最大值即可.
当0≤t≤20,t=15时,ymax=125,当20<t≤30,y随t的增大而减小.
∴在30天中的第15天,日交易额的最大值为125万元.
【名师点评】 数学建模是解决数学应用题的重要方法,是通过实验采集数据,从数据中抽象出规律近似描述这一实际问题的模型.建模的重点和难点是实际问题抽象为数学问题的过程,仔细分析语言描述,从中抽象出函数关系式,要求什么,它等于什么,如何去表达,怎样求解.本部分内容讲解结束Thank you!
指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为指数运算,其次若出现分式则要注意分子、分母因式分解以达到约分的目的,对数运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.【思路点拨】 利用幂指数及对数的运算性质.
【名师点评】 对幂值的计算,一般应尽可能把幂化为底数是质数的指数幂,再考虑同底数幂的运算法则及乘法公式.
对数运算中常常会逆用对数法则以达到化简的目的.对于不同底数的对数可以首先化为同底数的对数.函数的性质函数的单调性、奇偶性、最值问题是高考必考内容,通常综合考查函数的多个性质.②当-1<x1<x2<0时,x1-x2<0,0<x1x2<1,
∴x1x2-1<0.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
所以函数f(x)在(-1,0)上是减函数.
【名师点评】 (1)函数的奇偶性与单调性是函数的两个重要性质,解答问题时,要善于应用函数的观点,挖掘函数的奇偶性和单调性,并注意两者的联系.
(2)函数的单调性、奇偶性常与其他性质结合在一起进行考查,此类考查形式是常考点,应引起足够的重视.函数图象问题函数的图象是函数的重要表示方法.它具有直观性,通过函数图象能够掌握函数的重要性质.
利用数形结合解题有直观、明了、易懂的优点,在历届高考试题中,常出现有关函数图象和利用图象解题的试题.
所谓图象变换,就是把基本初等函数图象,通过平移、对称、翻折、伸缩等变换,变成复合函数的图象,因此要熟记基本函数图象,掌握变换的技巧方法. 已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数f2(x)的图象与直线y=x的两个交点间距离为8,f(x)=f1(x)+f2(x).
(1)求函数f(x)的表达式;
(2)求证:当a>3时,关于x的方程f(x)=f(a)有三个实数解.
【思路点拨】 本题从研究图象入手,直观地分析根的个数.构造基本初等函数是解题关键.【名师点评】 (1)熟记一次函数、二次函数、反比例函数、正比例函数、指数函数、对数函数的大致图象(关键点要准确).
(2)要有数形结合的意识“有数无形少直观,有形无数难入微”.函数的零点与方程的根的关系及应用根据函数零点的定义,函数y=f(x)的零点就是方程f(x)=0的根,判断一个函数是否有零点,有几个零点,就是判断方程f(x)=0是否有实根,有几个实根.从图象上说,函数的零点就是函数y=f(x)的图象与x轴的交点的横坐标.函数的零点、方程的根、函数图象与x轴的交点三者之间有着内在的本质联系,利用它们之间的关系,可以解决很多函数、方程与不等式的问题.在高考中有许多问题涉及三者的相互转化,思考时要多加注意.【名师点评】 求函数的零点或方程的根常用的方法有:
①直接法,即求f(x)=0的根;
②讨论函数y=f(x)的性质,画出它的图象,从而判定它与x轴的交点个数,就可以判定根的个数;
③利用根的存在性定理;
④函数与方程的思想应用,把方程转化成两个函数图象的交点问题.函数建模数学应用题是指带有一定生产、生活背景的数量化问题.解答数学应用题就是在阅读材料、理解题意的基础上,把实际问题转化为数学问题,建立相应的数学模型,再利用数学知识对模型进行分析、研究、解答,然后再把答案返回到实际问题中去,获取具有实际意义的结论.其基本程序如下: 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上;该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如下表所示:(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y表示该股票日交易额(万元),写出y关于t的函数关系式,并求在这30天中第几天日交易额最大,最大值是多少?
【思路点拨】 由图象和表格可直接写出函数关系式,由(1)(2)问的函数关系式相乘,可得第(3)问的函数关系式,再求最大值即可.
当0≤t≤20,t=15时,ymax=125,当20<t≤30,y随t的增大而减小.
∴在30天中的第15天,日交易额的最大值为125万元.
【名师点评】 数学建模是解决数学应用题的重要方法,是通过实验采集数据,从数据中抽象出规律近似描述这一实际问题的模型.建模的重点和难点是实际问题抽象为数学问题的过程,仔细分析语言描述,从中抽象出函数关系式,要求什么,它等于什么,如何去表达,怎样求解.本部分内容讲解结束Thank you!
