青岛版七年级数学下册 14.2 平面直角坐标系课件(共20张PPT)
文档属性
| 名称 | 青岛版七年级数学下册 14.2 平面直角坐标系课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 693.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-28 11:40:20 | ||
图片预览


文档简介
(共23张PPT)
14.2 平面直角坐标系
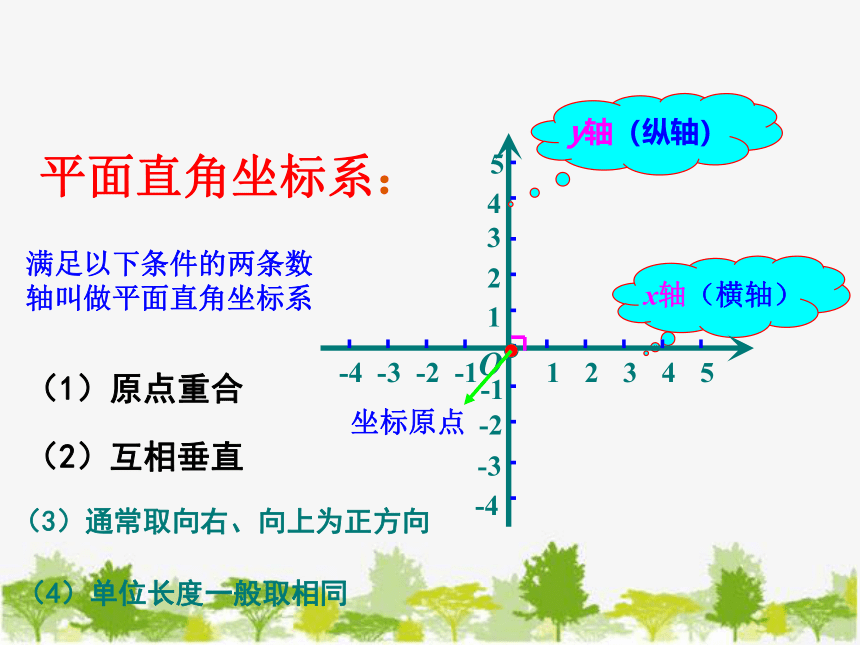
满足以下条件的两条数轴叫做平面直角坐标系
(1)原点重合
(2)互相垂直
x轴(横轴)
O
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y轴(纵轴)
坐标原点
(3)通常取向右、向上为正方向
(4)单位长度一般取相同
平面直角坐标系:
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
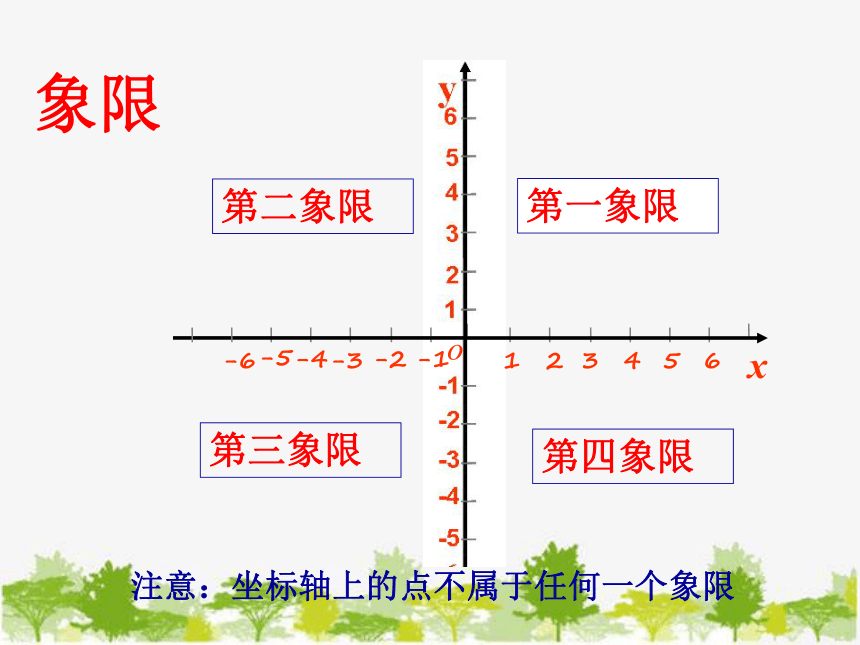
象限
第二象限
第一象限
第三象限
第四象限
注意:坐标轴上的点不属于任何一个象限
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
A·
过点A分别作x轴、y轴的垂线
垂足M在x轴上所表示的数为-2,
垂足N在y轴上表示的数为3 ,
我们就说A的横坐标为-2,
纵坐标为3。
有序数对(-2,3)就是点A的坐标
记作A(-2,3),
原点的做标记为(0,0)
M(-2,0),N(0,3)
如何确定点的坐标?
M
N
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(3,2)
p
y
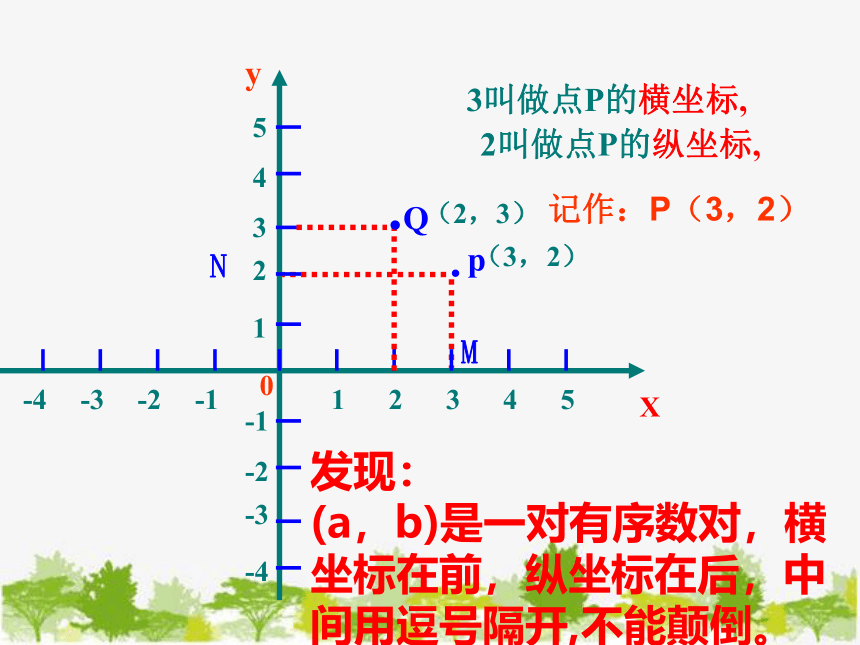
3叫做点P的横坐标,
2叫做点P的纵坐标,
X
记作:P(3,2)
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
.Q
(2,3)
发现:
(a,b)是一对有序数对,横坐标在前,纵坐标在后,中间用逗号隔开,不能颠倒。
N
M
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
坐标是有序
数对。
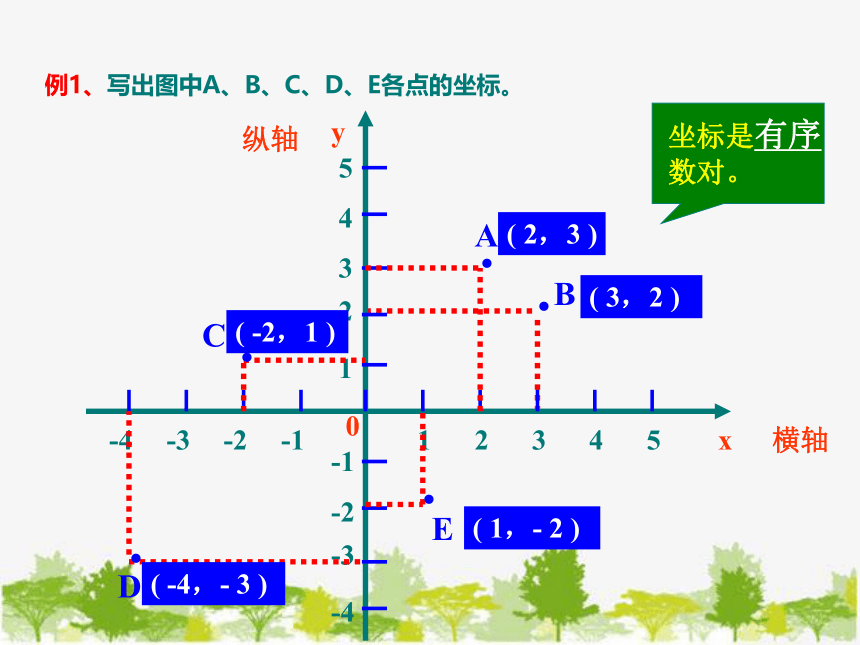
例1、写出图中A、B、C、D、E各点的坐标。
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
A·
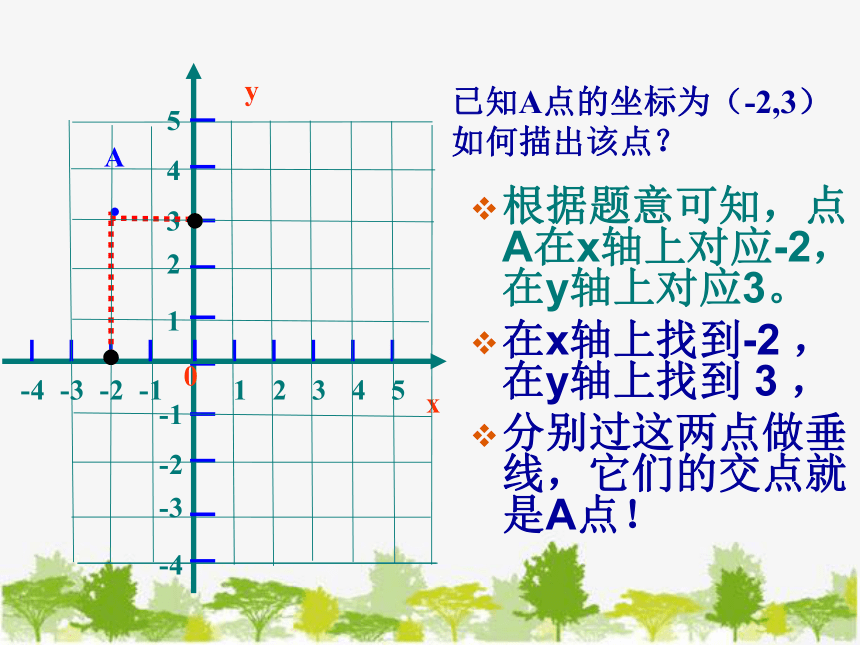
已知A点的坐标为(-2,3)
如何描出该点?
根据题意可知,点A在x轴上对应-2,在y轴上对应3。
在x轴上找到-2 ,在y轴上找到 3 ,
分别过这两点做垂线,它们的交点就是A点!
(2,-3)
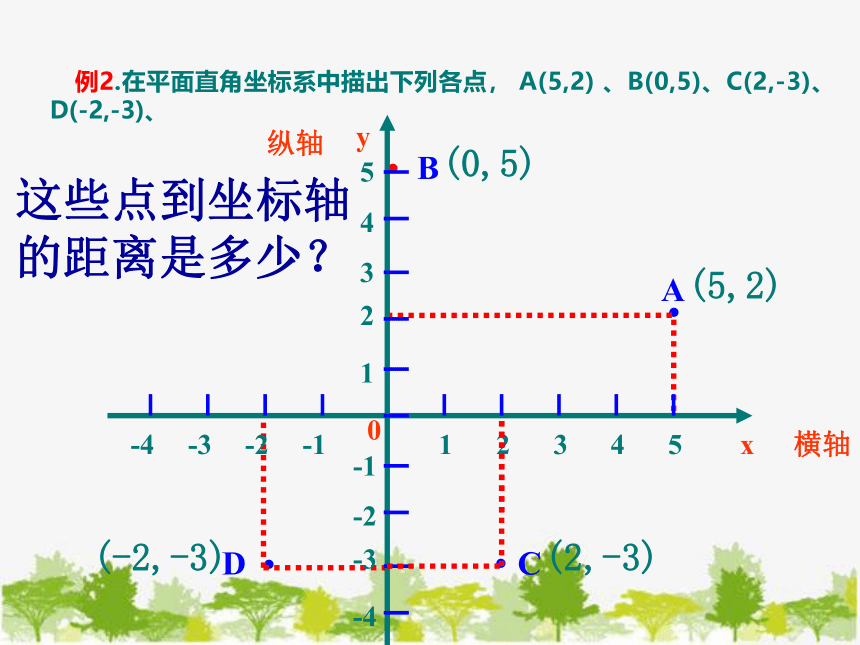
例2.在平面直角坐标系中描出下列各点, A(5,2) 、B(0,5)、C(2,-3)、 D(-2,-3)、
A
·
B
·
D
·
(0,5)
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
x
横轴
C
·
(5,2)
(-2,-3)
这些点到坐标轴
的距离是多少?
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
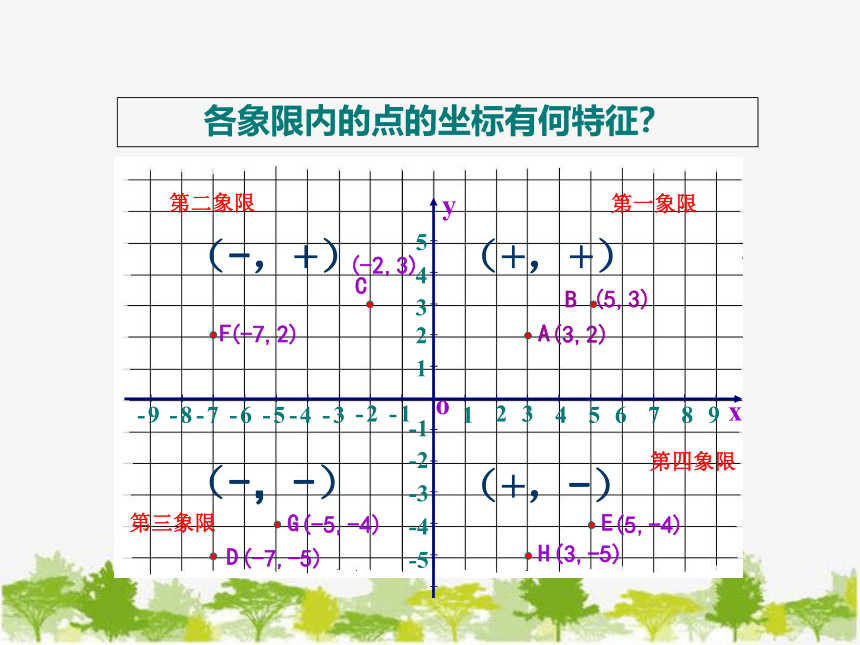
各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
第一象限
第二象限
第三象限
第四象限
4:几个象限内点的特点
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
考考你:1、请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5、2) B(3、-2) C(0、4), D(-6、0) E(1、8) F(0、0),
G(5、0),H(-6、-4)K(0、-3)
解:A在第二象限,
B在第四象限,
C在Y的正半轴,
E在第一象限,
D在X轴的负半轴,
F在原点,
G在X轴的正半轴,
H在第三象限,
K在Y轴的负半轴。
坐标轴上的点的坐标有何特点?
横轴上的点的纵坐标为0,表示为(x,0)
纵轴上的点的横坐标为0.表示为(0,y) 原点的坐标为(0,0)
结论
距离
P(a,b)到x轴的距离是_____
到y轴的距离是_____
︱b︱
︱a︱
.已知点P(3,a),并且P点到x轴的距离是2个单位长度,求P点的坐标。
分析:由一个点到x轴的距离是该点纵坐标的绝对值,所以a的绝对值等于2,这样a的值应等于±2。
解:因为P到X轴的距离是2 ,所以,a的值可以等于±2,因此P(3,2)或P(3,-2)。
平行于坐标轴的直线上的点的坐标有何特点?
结论
平行于y轴的直线上的点的横坐标相同,平行于x轴的直线上的点的纵坐标相同。
直角坐标系中点的坐标的特点
—
+
—
—
+
—
—
—
+
+
0
0
0
0
0
0
这节课主要学面直角坐标系的有关概念和一个最基本的问题,坐标平面内的点与有序数对是一一对应的。
1. 会根据坐标找点,会由坐标系内的点写坐标
2.掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限:(+, +)
第二象限:(—, +)
第三象限:(—,—)
第四象限:(+, —)
小结
巩固练习:
1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
4.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是________。
3.点 M(- 8,12)到 x轴的距离是_________,
到 y轴的距离是________.
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 _______________。
四
三
y
-1
(4,0)或(-4,0)
12
8
(-1.5,-2)
7.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
8.若点(a,b)在第二象限,则a的取值范围是_____,b的取值范围________。
9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在( ). (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________。
第二或四象限
B
a<0
b>0
B
思考:
设点M(a,b)为平面直角坐标系中的点
当a>0,b<0时点M位于第几象限?
当ab>0时,点M位于第几象限?
当ab=0时,点M位于什么位置?
当a为任意数时,且b<0时,点M直角坐标系中的位置是什么?
14.2 平面直角坐标系
满足以下条件的两条数轴叫做平面直角坐标系
(1)原点重合
(2)互相垂直
x轴(横轴)
O
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y轴(纵轴)
坐标原点
(3)通常取向右、向上为正方向
(4)单位长度一般取相同
平面直角坐标系:
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
象限
第二象限
第一象限
第三象限
第四象限
注意:坐标轴上的点不属于任何一个象限
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
A·
过点A分别作x轴、y轴的垂线
垂足M在x轴上所表示的数为-2,
垂足N在y轴上表示的数为3 ,
我们就说A的横坐标为-2,
纵坐标为3。
有序数对(-2,3)就是点A的坐标
记作A(-2,3),
原点的做标记为(0,0)
M(-2,0),N(0,3)
如何确定点的坐标?
M
N
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(3,2)
p
y
3叫做点P的横坐标,
2叫做点P的纵坐标,
X
记作:P(3,2)
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
.Q
(2,3)
发现:
(a,b)是一对有序数对,横坐标在前,纵坐标在后,中间用逗号隔开,不能颠倒。
N
M
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
坐标是有序
数对。
例1、写出图中A、B、C、D、E各点的坐标。
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
A·
已知A点的坐标为(-2,3)
如何描出该点?
根据题意可知,点A在x轴上对应-2,在y轴上对应3。
在x轴上找到-2 ,在y轴上找到 3 ,
分别过这两点做垂线,它们的交点就是A点!
(2,-3)
例2.在平面直角坐标系中描出下列各点, A(5,2) 、B(0,5)、C(2,-3)、 D(-2,-3)、
A
·
B
·
D
·
(0,5)
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
x
横轴
C
·
(5,2)
(-2,-3)
这些点到坐标轴
的距离是多少?
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
第一象限
第二象限
第三象限
第四象限
4:几个象限内点的特点
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
考考你:1、请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5、2) B(3、-2) C(0、4), D(-6、0) E(1、8) F(0、0),
G(5、0),H(-6、-4)K(0、-3)
解:A在第二象限,
B在第四象限,
C在Y的正半轴,
E在第一象限,
D在X轴的负半轴,
F在原点,
G在X轴的正半轴,
H在第三象限,
K在Y轴的负半轴。
坐标轴上的点的坐标有何特点?
横轴上的点的纵坐标为0,表示为(x,0)
纵轴上的点的横坐标为0.表示为(0,y) 原点的坐标为(0,0)
结论
距离
P(a,b)到x轴的距离是_____
到y轴的距离是_____
︱b︱
︱a︱
.已知点P(3,a),并且P点到x轴的距离是2个单位长度,求P点的坐标。
分析:由一个点到x轴的距离是该点纵坐标的绝对值,所以a的绝对值等于2,这样a的值应等于±2。
解:因为P到X轴的距离是2 ,所以,a的值可以等于±2,因此P(3,2)或P(3,-2)。
平行于坐标轴的直线上的点的坐标有何特点?
结论
平行于y轴的直线上的点的横坐标相同,平行于x轴的直线上的点的纵坐标相同。
直角坐标系中点的坐标的特点
—
+
—
—
+
—
—
—
+
+
0
0
0
0
0
0
这节课主要学面直角坐标系的有关概念和一个最基本的问题,坐标平面内的点与有序数对是一一对应的。
1. 会根据坐标找点,会由坐标系内的点写坐标
2.掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
第一象限:(+, +)
第二象限:(—, +)
第三象限:(—,—)
第四象限:(+, —)
小结
巩固练习:
1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
4.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是________。
3.点 M(- 8,12)到 x轴的距离是_________,
到 y轴的距离是________.
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是 _______________。
四
三
y
-1
(4,0)或(-4,0)
12
8
(-1.5,-2)
7.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
8.若点(a,b)在第二象限,则a的取值范围是_____,b的取值范围________。
9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在( ). (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________。
第二或四象限
B
a<0
b>0
B
思考:
设点M(a,b)为平面直角坐标系中的点
当a>0,b<0时点M位于第几象限?
当ab>0时,点M位于第几象限?
当ab=0时,点M位于什么位置?
当a为任意数时,且b<0时,点M直角坐标系中的位置是什么?
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
