11.2.3三角形全等的判定(SAS)
文档属性
| 名称 | 11.2.3三角形全等的判定(SAS) |  | |
| 格式 | zip | ||
| 文件大小 | 343.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-13 16:12:20 | ||
图片预览


文档简介
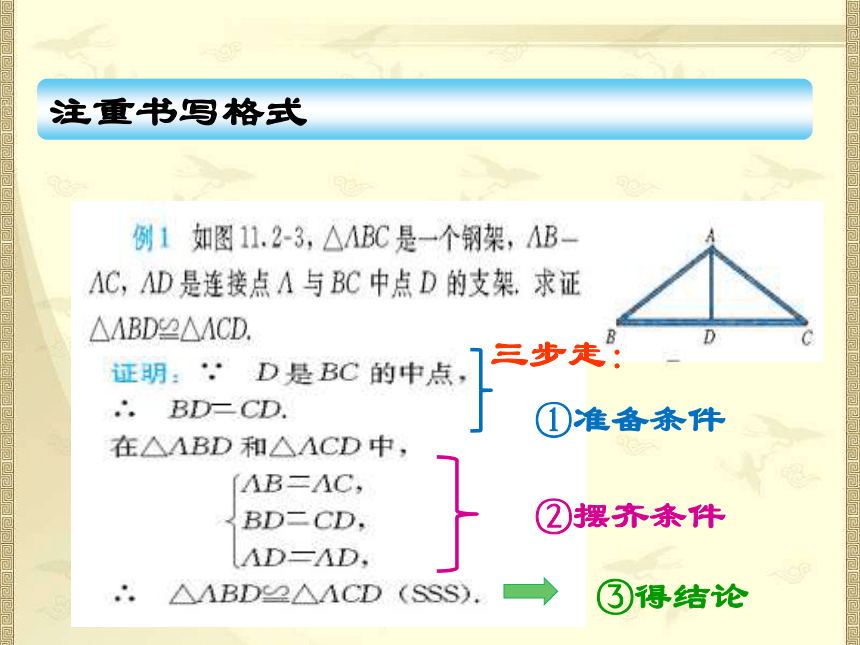
课件24张PPT。§11.2 三角形全等的判定(二) 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为: 三角形全等判定方法1
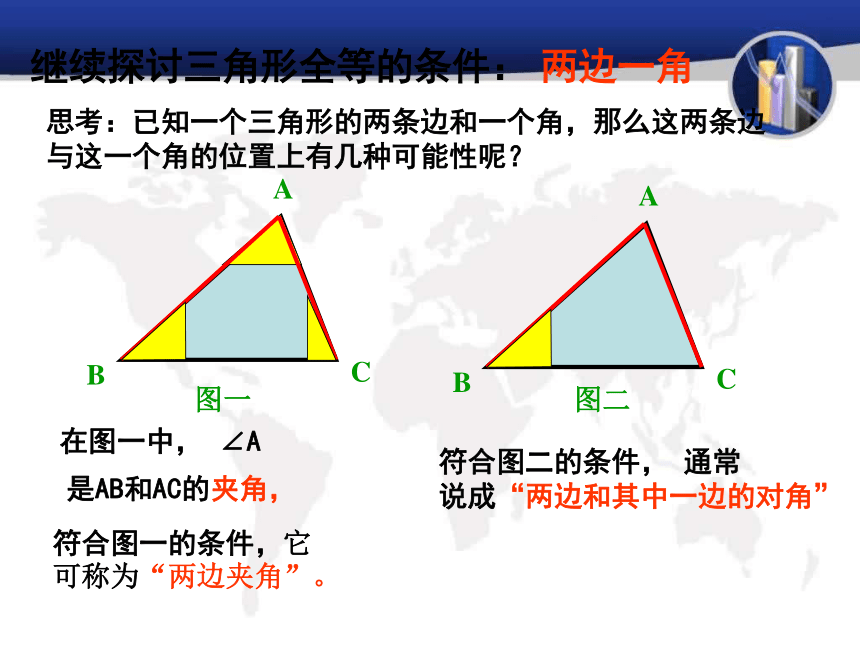
三步走:①准备条件②摆齐条件③得结论注重书写格式除了SSS外,还有其他情况吗?继续探索三角形全等的条件.思考(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件中的三个时,有四种情况:SSS不能!?继续探讨三角形全等的条件:两边一角思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?图一图二在图一中, ∠A是AB和AC的夹角,符合图一的条件,它可称为“两边夹角”。符合图二的条件, 通常
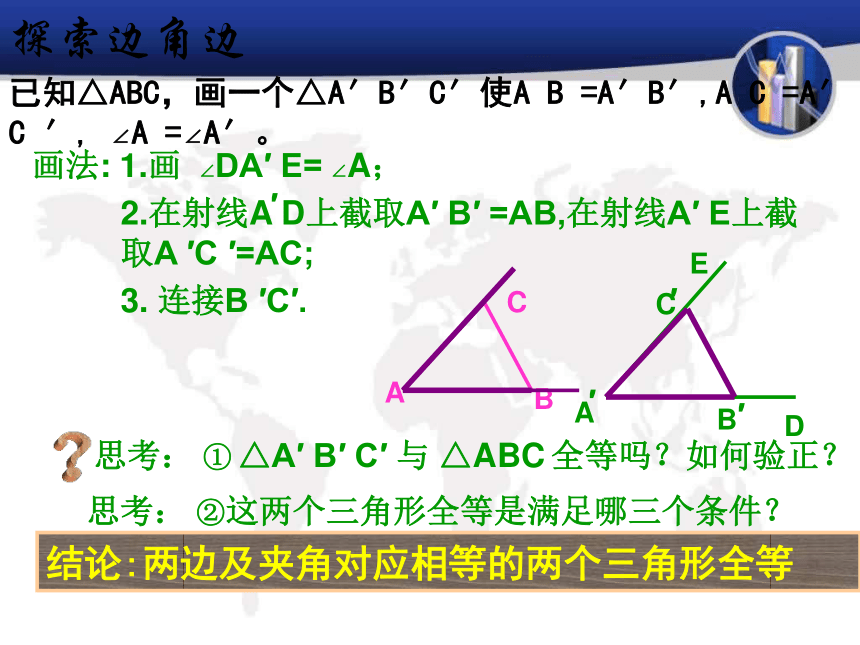
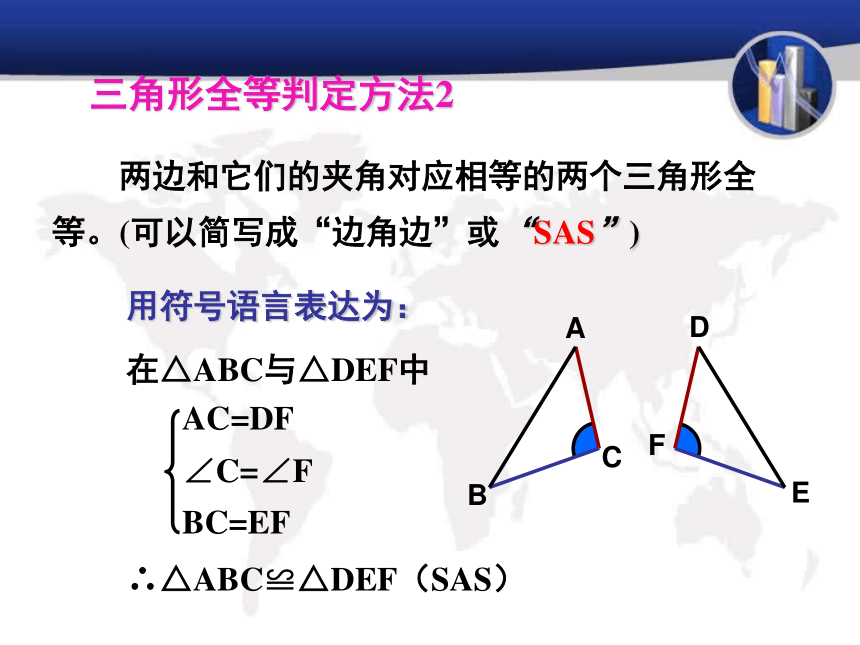
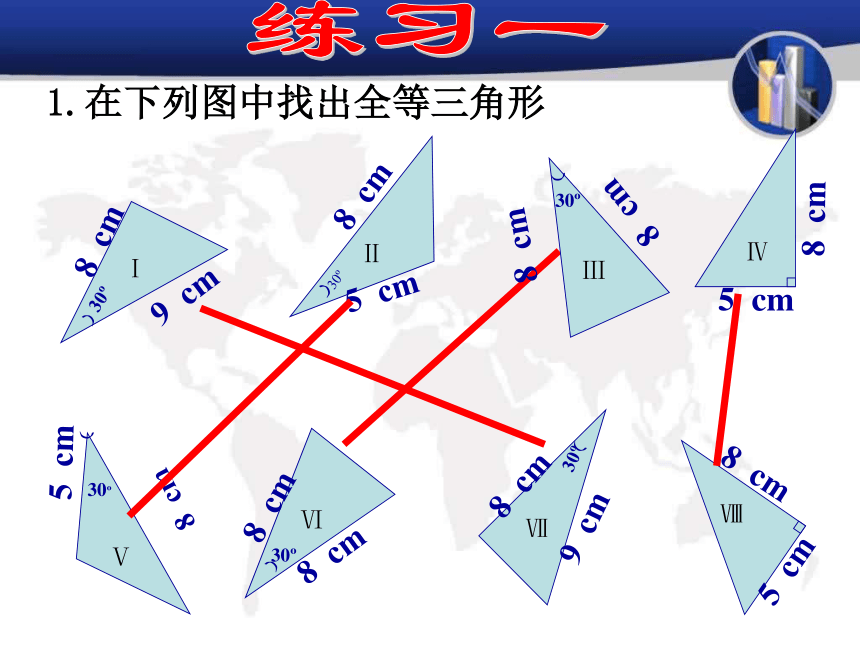
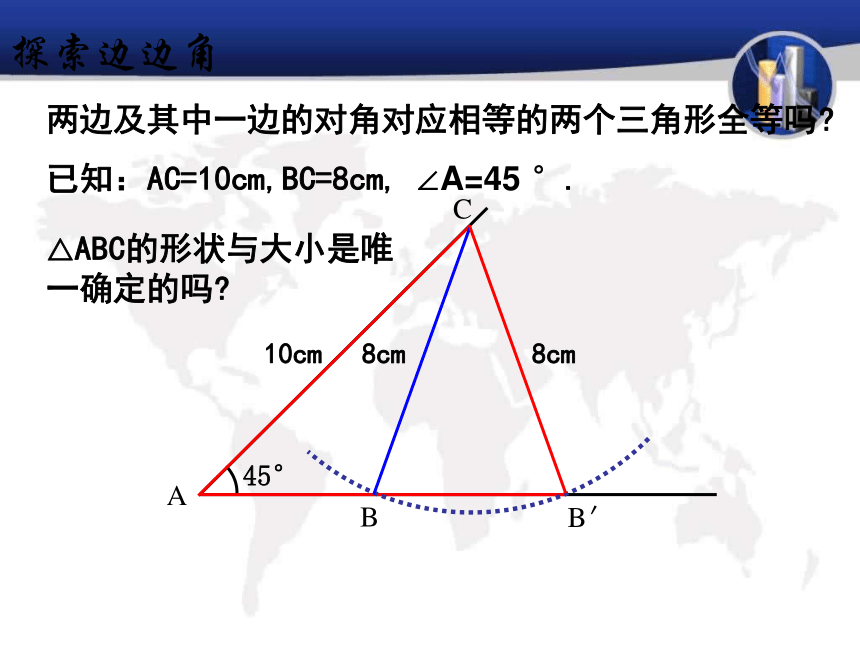
说成“两边和其中一边的对角”已知△ABC,画一个△A′B′C′使A B =A′B′,A C =A′ C ′, ∠A =∠A′。结论:两边及夹角对应相等的两个三角形全等?思考: ① △A′ B′ C′ 与 △ABC 全等吗?如何验正?画法: 1.画 ∠DA′ E= ∠A;2.在射线A D上截取A′ B′ =AB,在射线A′ E上截取A ′C ′=AC;3. 连接B ′C′.′ACBA′EDCB′′思考: ②这两个三角形全等是满足哪三个条件?探索边角边 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA1.在下列图中找出全等三角形练习一探索边边角两边及其中一边的对角对应相等的两个三角形全等吗?已知:AC=10cm,BC=8cm, ∠A=45 °.△ABC的形状与大小是唯一确定的吗?探索边边角SSA不存在显然: △ABC与△AB’C不全等ABDABCSSA不能判定全等两边及一角对应相等的两个三角形全等吗?①两边及夹角对应相等的两个三角形全等(SAS);②两边及其中一边的的对角对应相等的两个三角形不一定全等.③ 现在你知道哪些三角形全等的判定方法?SSS, SAS例. 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。证明:在△ABC与△BAD中 AC=BD
∠CAB=∠DBA
AB=BA∴△ABC≌△BAD(SAS)(已知)(已知)(公共边)∴BC=AD (全等三角形的对应边相等) 因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。归纳C在下列推理中填写需要补充
的条件,使结论成立:
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS练习一(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSA S练习二AD=ADBD=CDS2.如图,要证△ACB≌ △ADB ,至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CAB= ∠ DABAC=ADSBC=BD3.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。●●练习三●●例.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件?同步练习 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为: 三角形全等判定方法1 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBAABDABCSSA不能判定全等谢谢合作 再见
三步走:①准备条件②摆齐条件③得结论注重书写格式除了SSS外,还有其他情况吗?继续探索三角形全等的条件.思考(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件中的三个时,有四种情况:SSS不能!?继续探讨三角形全等的条件:两边一角思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?图一图二在图一中, ∠A是AB和AC的夹角,符合图一的条件,它可称为“两边夹角”。符合图二的条件, 通常
说成“两边和其中一边的对角”已知△ABC,画一个△A′B′C′使A B =A′B′,A C =A′ C ′, ∠A =∠A′。结论:两边及夹角对应相等的两个三角形全等?思考: ① △A′ B′ C′ 与 △ABC 全等吗?如何验正?画法: 1.画 ∠DA′ E= ∠A;2.在射线A D上截取A′ B′ =AB,在射线A′ E上截取A ′C ′=AC;3. 连接B ′C′.′ACBA′EDCB′′思考: ②这两个三角形全等是满足哪三个条件?探索边角边 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA1.在下列图中找出全等三角形练习一探索边边角两边及其中一边的对角对应相等的两个三角形全等吗?已知:AC=10cm,BC=8cm, ∠A=45 °.△ABC的形状与大小是唯一确定的吗?探索边边角SSA不存在显然: △ABC与△AB’C不全等ABDABCSSA不能判定全等两边及一角对应相等的两个三角形全等吗?①两边及夹角对应相等的两个三角形全等(SAS);②两边及其中一边的的对角对应相等的两个三角形不一定全等.③ 现在你知道哪些三角形全等的判定方法?SSS, SAS例. 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。证明:在△ABC与△BAD中 AC=BD
∠CAB=∠DBA
AB=BA∴△ABC≌△BAD(SAS)(已知)(已知)(公共边)∴BC=AD (全等三角形的对应边相等) 因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。归纳C在下列推理中填写需要补充
的条件,使结论成立:
(1)如图,在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )∠ AOB∠ DOC对顶角相等SAS练习一(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSA S练习二AD=ADBD=CDS2.如图,要证△ACB≌ △ADB ,至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CAB= ∠ DABAC=ADSBC=BD3.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。●●练习三●●例.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件?同步练习 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为: 三角形全等判定方法1 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBAABDABCSSA不能判定全等谢谢合作 再见
