平行线的判定与性质习题课
文档属性
| 名称 | 平行线的判定与性质习题课 |  | |
| 格式 | zip | ||
| 文件大小 | 123.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-13 16:23:07 | ||
图片预览


文档简介
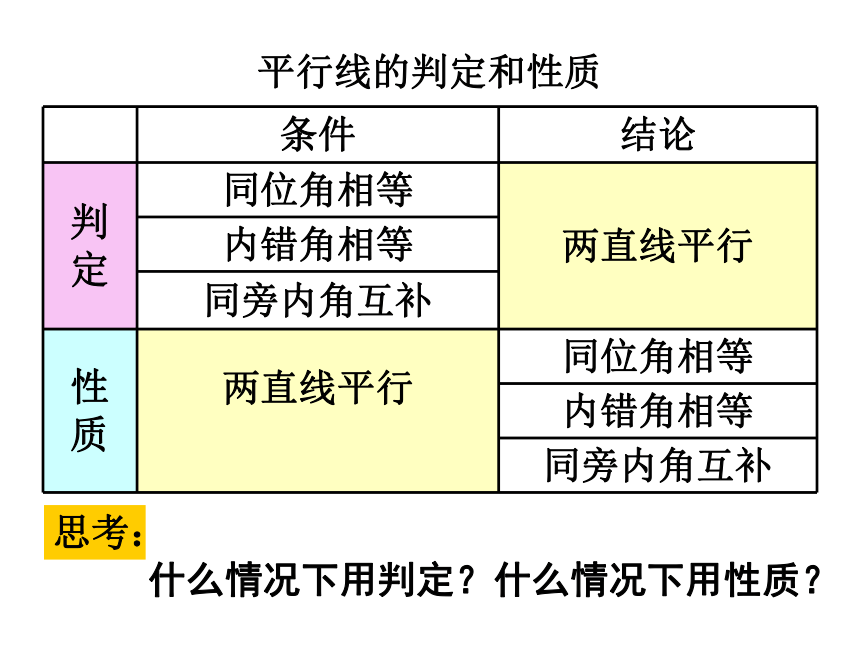
课件18张PPT。平行线的判定与性质习题课复习一、平行线的判定方法:
二、平行线的性质:
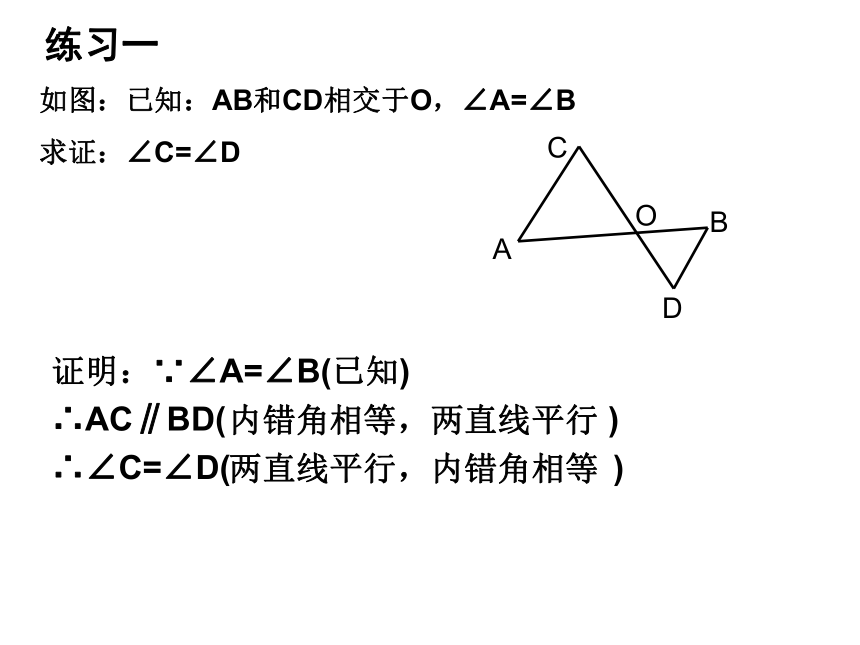
三、它们有什么不同?思考:什么情况下用判定?什么情况下用性质?平行线的判定和性质练习一证明:∵∠A=∠B(已知)
∴AC∥BD( )
∴∠C=∠D( )如图:已知:AB和CD相交于O,∠A=∠B
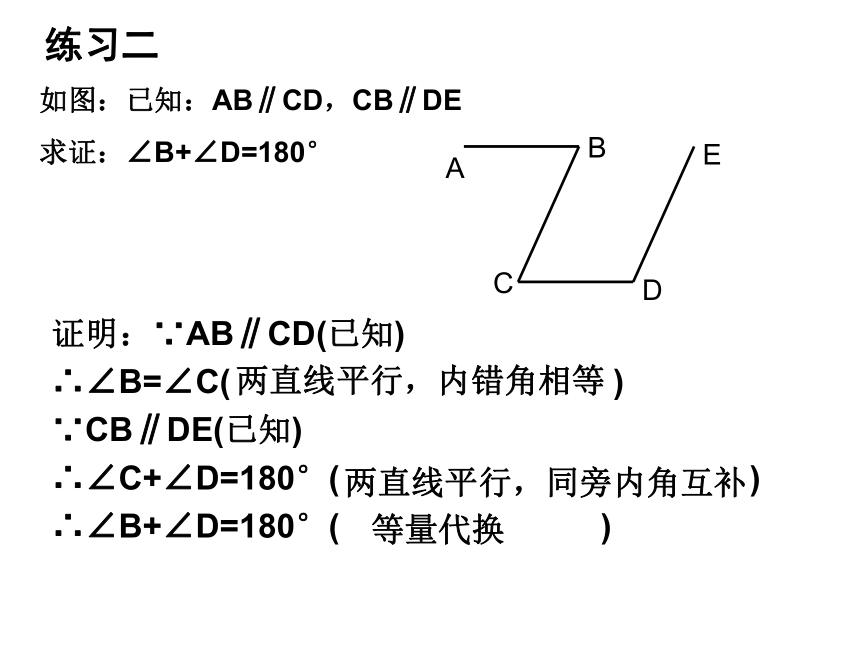
求证:∠C=∠DACOBD内错角相等,两直线平行两直线平行,内错角相等练习二证明:∵AB∥CD(已知)
∴∠B=∠C( )
∵CB∥DE(已知)
∴∠C+∠D=180°( )
∴∠B+∠D=180°( )如图:已知:AB∥CD,CB∥DE
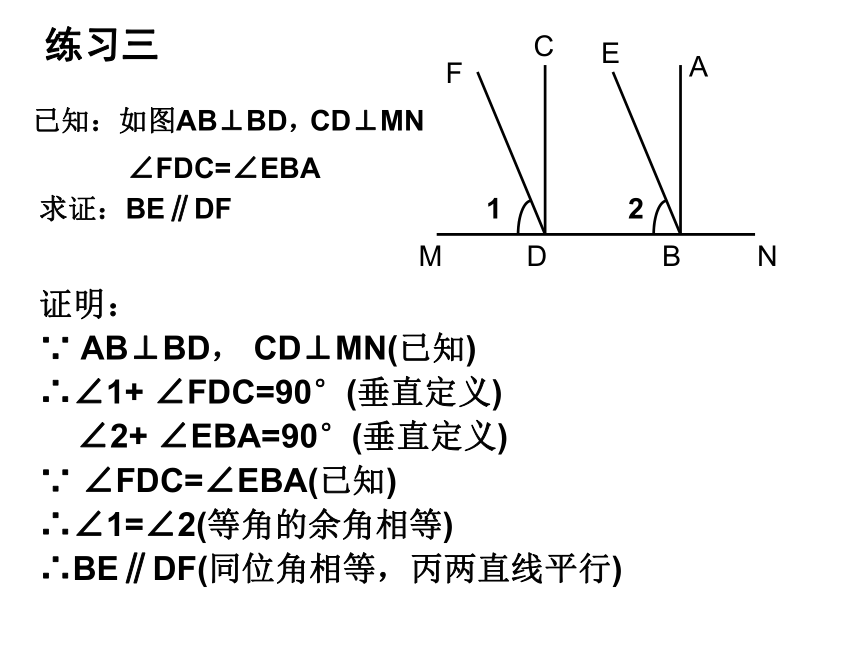
求证:∠B+∠D=180°ABCED两直线平行,同旁内角互补两直线平行,内错角相等等量代换AECFMDBN已知:如图AB⊥BD,CD⊥MN∠FDC=∠EBA证明:
∵ AB⊥BD, CD⊥MN(已知)
∴∠1+ ∠FDC=90°(垂直定义)
∠2+ ∠EBA=90°(垂直定义)
∵ ∠FDC=∠EBA(已知)
∴∠1=∠2(等角的余角相等)
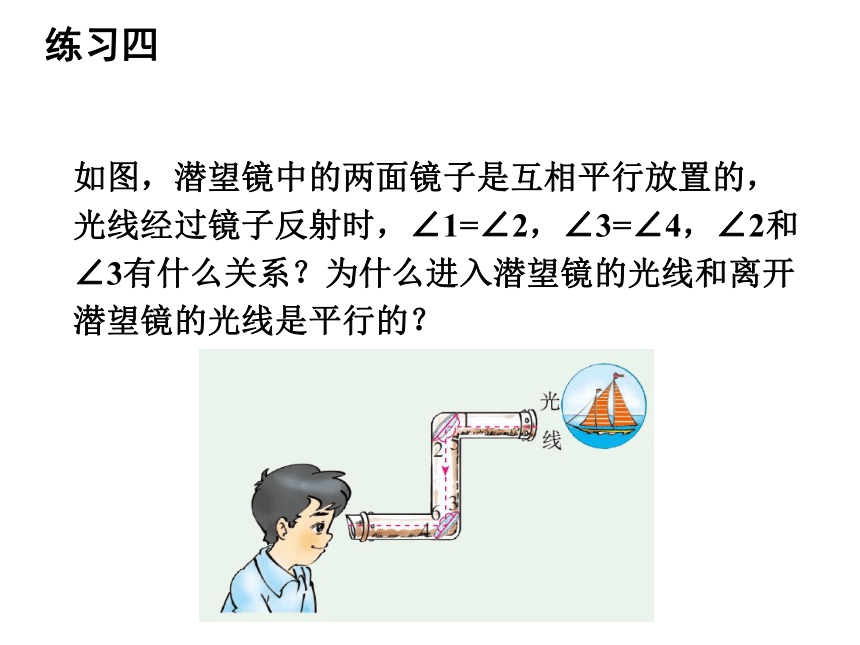
∴BE∥DF(同位角相等,丙两直线平行)21练习三求证:BE∥DF如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?练习四已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.
猜想:∠2和∠3有什么关系,并说明理由;
试说明:PM∥NQ.答:∠2=∠3.
理由如下:
∵ AB∥CD ,
∴ ∠2=∠3(两直线平行,内错角相等).练习四已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.
试说明:PM∥NQ.理由如下:
∵∠1=∠2 ,∠3=∠4(已知)
又∵∠2=∠3.(已证)
∴∠1=∠2 =∠3=∠4.
∵∠1+∠2 +∠5=180o,∠3+∠4 +∠6=180o,
∴∠5=∠6.(等式性质)
∵∠5和∠6是内错角,
∴ PM∥NQ (内错角相等,两直线平行).练习四解:∵AB∥CD(已知)
∴ ∠BAC+∠ACD=180°( )
∵AB∥CD(已知)
∴ ∠DCE+∠CEF=180°( )
∴ ∠BAC+∠ACE+∠CEF= ∠BAC+∠ACD
+ ∠DCE+∠CEF
=180°+180°=360°练习五如图:已知:AB∥CD∥EF
求:∠BAC+∠ACE+∠CEF的度数ABDFEC两直线平行,同旁内角互补两直线平行,同旁内角互补ECDBAF练习六如图:已知:AB∥CD,EF∥AB
问:∠AFC、∠A和∠C之间有何关系?理由:∵AB∥CD,EF∥AB(已知)
∴CD∥EF( )
∴ ∠1=∠C( )
∵AB∥EF(已知)
∴ ∠2=∠A( )
又∵ ∠AFC=∠1+∠2( )
∴∠AFC=∠A+∠C( )答: ∠AFC=∠A+∠C如果两直线都和第三条直线平行,那么这两条直线也平行两直线平行,内错角相等两直线平行,内错角相等角的和差定义等量代换练习六变式如图:已知:a∥b,∠1=105°,∠2=140°
求∠α的度数答: ∠α的度数为65°还有没有其他的方法?解:过P点作c∥b
∵a∥b
∴a∥b∥c
∴∠1+∠3=180°,∠2+∠4=180°
∵ ∠1=105°,∠2=140°
∴∠3=75°∠4=40°
∴ ∠α=180°-∠3-∠4=180°-75°-40°=65°P练习六变式如图:已知:a∥b,∠1=105°,∠2=140°
求∠α的度数答: ∠α的度数为65°还有没有其他的方法?练习六变式如图:已知:a∥b,∠1=105°,∠2=140°
求∠α的度数答: ∠α的度数为65°当然,除这之外还有其它方法,我们就不再一一研究。如果一个角的两边分别平行于另一个角的两边,那么这两个角有什么关系?练习七由此可得:
这样的两个角相等。如果一个角的两边分别平行于另一个角的两边,那么这两个角有什么关系?练习七由此可得:
这样的两个角互补。所以说:如果一个角的两边分别平行于另一个角的两
边,那么这两个角___________相等或互补布置作业:课本P37第13题。
二、平行线的性质:
三、它们有什么不同?思考:什么情况下用判定?什么情况下用性质?平行线的判定和性质练习一证明:∵∠A=∠B(已知)
∴AC∥BD( )
∴∠C=∠D( )如图:已知:AB和CD相交于O,∠A=∠B
求证:∠C=∠DACOBD内错角相等,两直线平行两直线平行,内错角相等练习二证明:∵AB∥CD(已知)
∴∠B=∠C( )
∵CB∥DE(已知)
∴∠C+∠D=180°( )
∴∠B+∠D=180°( )如图:已知:AB∥CD,CB∥DE
求证:∠B+∠D=180°ABCED两直线平行,同旁内角互补两直线平行,内错角相等等量代换AECFMDBN已知:如图AB⊥BD,CD⊥MN∠FDC=∠EBA证明:
∵ AB⊥BD, CD⊥MN(已知)
∴∠1+ ∠FDC=90°(垂直定义)
∠2+ ∠EBA=90°(垂直定义)
∵ ∠FDC=∠EBA(已知)
∴∠1=∠2(等角的余角相等)
∴BE∥DF(同位角相等,丙两直线平行)21练习三求证:BE∥DF如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?练习四已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.
猜想:∠2和∠3有什么关系,并说明理由;
试说明:PM∥NQ.答:∠2=∠3.
理由如下:
∵ AB∥CD ,
∴ ∠2=∠3(两直线平行,内错角相等).练习四已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.
试说明:PM∥NQ.理由如下:
∵∠1=∠2 ,∠3=∠4(已知)
又∵∠2=∠3.(已证)
∴∠1=∠2 =∠3=∠4.
∵∠1+∠2 +∠5=180o,∠3+∠4 +∠6=180o,
∴∠5=∠6.(等式性质)
∵∠5和∠6是内错角,
∴ PM∥NQ (内错角相等,两直线平行).练习四解:∵AB∥CD(已知)
∴ ∠BAC+∠ACD=180°( )
∵AB∥CD(已知)
∴ ∠DCE+∠CEF=180°( )
∴ ∠BAC+∠ACE+∠CEF= ∠BAC+∠ACD
+ ∠DCE+∠CEF
=180°+180°=360°练习五如图:已知:AB∥CD∥EF
求:∠BAC+∠ACE+∠CEF的度数ABDFEC两直线平行,同旁内角互补两直线平行,同旁内角互补ECDBAF练习六如图:已知:AB∥CD,EF∥AB
问:∠AFC、∠A和∠C之间有何关系?理由:∵AB∥CD,EF∥AB(已知)
∴CD∥EF( )
∴ ∠1=∠C( )
∵AB∥EF(已知)
∴ ∠2=∠A( )
又∵ ∠AFC=∠1+∠2( )
∴∠AFC=∠A+∠C( )答: ∠AFC=∠A+∠C如果两直线都和第三条直线平行,那么这两条直线也平行两直线平行,内错角相等两直线平行,内错角相等角的和差定义等量代换练习六变式如图:已知:a∥b,∠1=105°,∠2=140°
求∠α的度数答: ∠α的度数为65°还有没有其他的方法?解:过P点作c∥b
∵a∥b
∴a∥b∥c
∴∠1+∠3=180°,∠2+∠4=180°
∵ ∠1=105°,∠2=140°
∴∠3=75°∠4=40°
∴ ∠α=180°-∠3-∠4=180°-75°-40°=65°P练习六变式如图:已知:a∥b,∠1=105°,∠2=140°
求∠α的度数答: ∠α的度数为65°还有没有其他的方法?练习六变式如图:已知:a∥b,∠1=105°,∠2=140°
求∠α的度数答: ∠α的度数为65°当然,除这之外还有其它方法,我们就不再一一研究。如果一个角的两边分别平行于另一个角的两边,那么这两个角有什么关系?练习七由此可得:
这样的两个角相等。如果一个角的两边分别平行于另一个角的两边,那么这两个角有什么关系?练习七由此可得:
这样的两个角互补。所以说:如果一个角的两边分别平行于另一个角的两
边,那么这两个角___________相等或互补布置作业:课本P37第13题。
