沪科版八年级数学下册 19.3 矩形、菱形、正方形(第5课时)(共34张PPT)
文档属性
| 名称 | 沪科版八年级数学下册 19.3 矩形、菱形、正方形(第5课时)(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 07:48:01 | ||
图片预览




文档简介
(共34张PPT)
第5课时 正方形性质与判定
沪科版数学八年级下册
19.3 矩形、菱形、正方形
教学目标
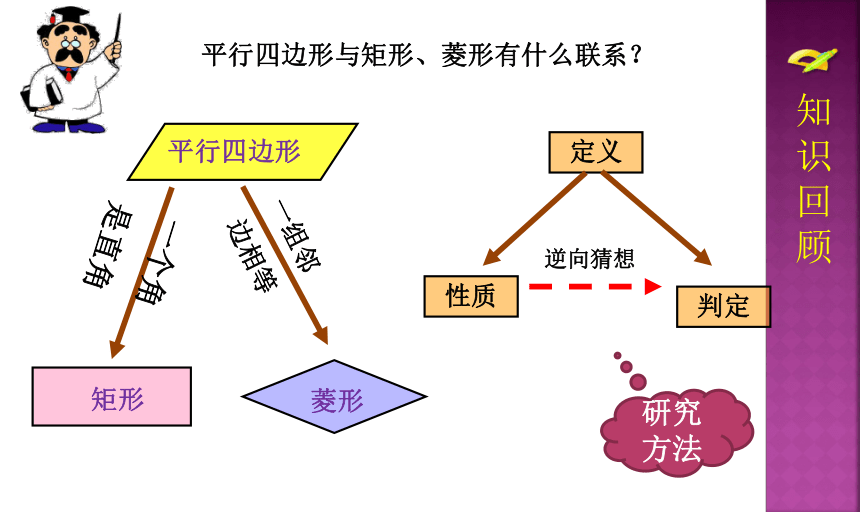
平行四边形与矩形、菱形有什么联系?
性质
定义
判定
逆向猜想
一个角
是直角
一组邻
边相等
平行四边形
矩形
菱形
知识回顾
研究方法
正方形
正方形
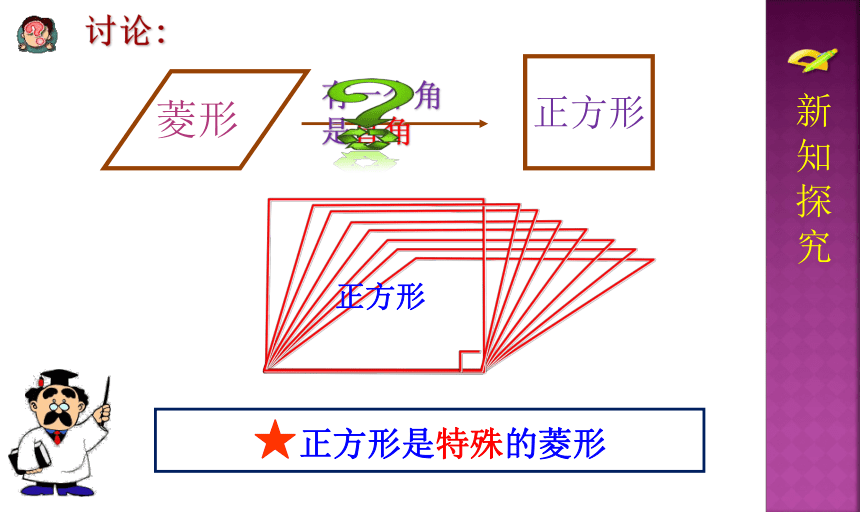
菱形
有一个角是直角
★正方形是特殊的菱形
讨论:
新知探究
A
B
C
D
讨论:
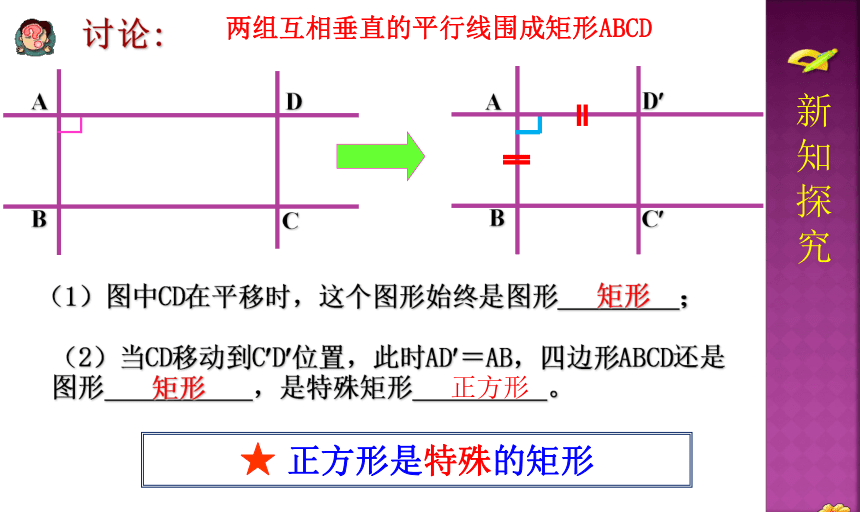
(1)图中CD在平移时,这个图形始终是图形 ;
(2)当CD移动到C D 位置,此时AD =AB,四边形ABCD还是图形 ,是特殊矩形 。
A
B
C
D
★ 正方形是特殊的矩形
两组互相垂直的平行线围成矩形ABCD
矩形
矩形
正方形
新知探究
有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
一、正方形的定义:
_______________的菱形是正方形
_______________的矩形是正方形
由正方形的定义可知:
有一个角是直角
有一组邻边相等
正方形既是菱形,又是矩形
新知讲解
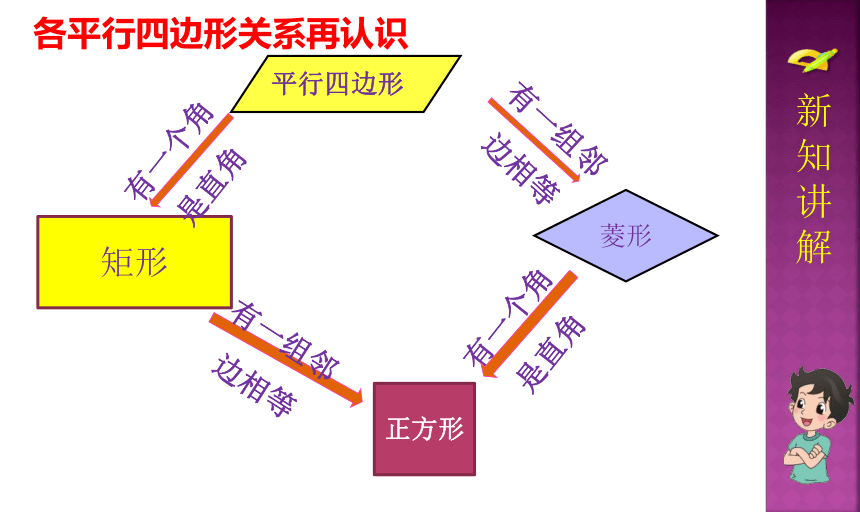
矩形
正方形
有一组邻边相等
各平行四边形关系再认识
平行四边形
菱形
有一组邻边相等
有一个角是直角
有一个角是直角
新知讲解
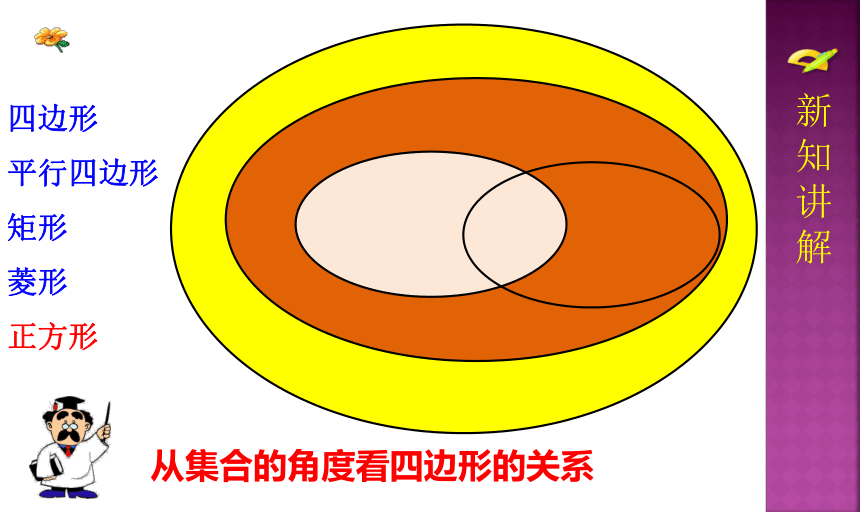
四边形
平行四边形
矩形
菱形
正方形
从集合的角度看四边形的关系
新知讲解
正方形的性质
正方形即是特殊的矩形又是特殊的菱形。
正方形具有矩形性质,同时也具有菱形形性质。
新知讲解
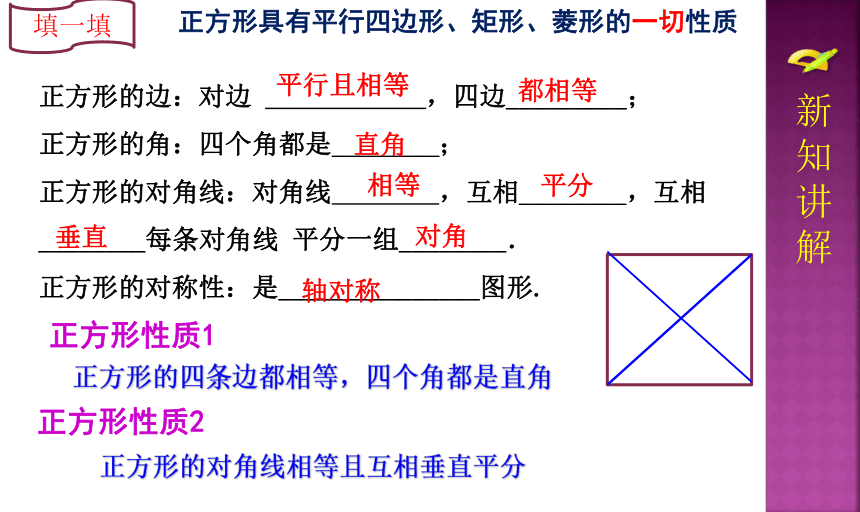
正方形的边:对边 ,四边_________;
正方形的角:四个角都是________;
正方形的对角线:对角线 ,互相________,互相________每条对角线 平分一组________.
正方形的对称性:是_______________图形.
直角
都相等
平行且相等
轴对称
平分
对角
相等
垂直
填一填
正方形性质1
正方形具有平行四边形、矩形、菱形的一切性质
正方形的四条边都相等,四个角都是直角
正方形性质2
正方形的对角线相等且互相垂直平分
新知讲解
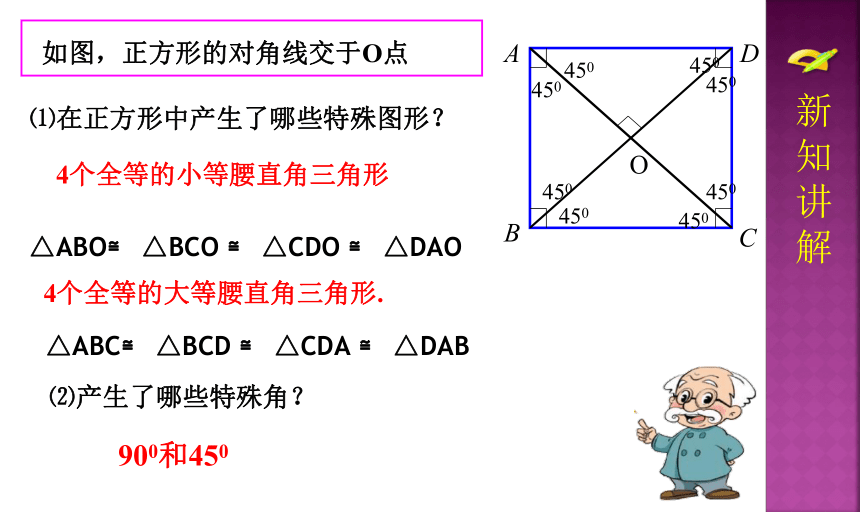
⑵产生了哪些特殊角?
D
O
A
B
C
450
450
450
450
450
450
450
450
4个全等的小等腰直角三角形
900和450
如图,正方形的对角线交于O点
⑴在正方形中产生了哪些特殊图形?
△ABO≌ △BCO ≌ △CDO ≌ △DAO
4个全等的大等腰直角三角形.
△ABC≌ △BCD ≌ △CDA ≌ △DAB
新知讲解
1、正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分
C、对角互补.
D、对角线相等.
2、正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
练习:
随堂练习
3.菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分
B.对角线相等且互相垂直平分
C.对角线互相平分
D.四条边相等,四个角相等
C
随堂练习
正方形的判定
特殊的菱形
特殊的矩形
新知讲解
正方形的判定方法
(可从平行四边形、矩形、菱形为基础)
平行四边形
正方形
一组邻边相等
一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
从边和角看
新知讲解
正方形的判定方法
(可从平行四边形、矩形、菱形为基础)
平行四边形
正方形
对角线相等
对角线垂直
1、
正方形
菱形
2、
对角线相等
矩形
3、
对角线互相垂直
正方形
从对角线看
新知讲解
下列说法对吗
(1)四个角都相等的四边形是正方形( )
(2)四条边都相等的四边形是正方形( )
(3)对角线相等的菱形是正方形( )
(4)对角线互相垂直的矩形是正方形( )
对
错
矩 形
错
菱 形
对
随堂练习
(5)对角线垂直且相等的四边形是正方形( )
(6)四边相等,有一角是直角的四边形是正方形( )
(7) 正方形的一条对角线把正方形分成两个全等的等腰 直角三角形( )
(8) 正方形是轴对称图形,一共有2条对称轴( )
下列说法对吗
错
对
对
错
4条对称轴
随堂练习
例1· AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:EC=EF=FB
A
B
C
D
E
F
┌
证明: ∵ 四边形ABCD是正方形
∴∠B=900 ∠ACB=450
∵∠AEF=900 AB=AE
∴△ABF≌△AFE(HL)
∴BF=EF
又∵∠FEC=900
∴∠EFC=450
∴EC=EF(等角对等边)
∴BF=EF=EC
例题讲解
已知2:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
A
B
C
D
E
G
┌
F
O
证明:
∵ 四边形ABCD是正方形,
∴ ∠AOE=∠DOF=90°,AO=DO
(正方形的对角线垂直平分且相等).
∵ DG⊥AE,
∴ ∠EAO+∠AEO=∠EDG+∠AEO=90°.
∴ ∠EAO=∠FDO.
∴ △AEO ≌△DFO.(ASA)
∴ OE=OF.
例题讲解
例3、已知:如图,四边形ABCD是正方形,分别过点A、C两点l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点
求证:四边形PQMN是正方形.
A
B
C
D
Q
M
N
P
l1
l2
3
2
1
证明:∵PN⊥l1,QM⊥l1,
∴PN∥QM,∠PNM=90°
∵PQ∥NM,∴四边形PQMN是矩形
∵四边形ABCD是正方形
∴∠BAD=∠ADC=90°,AB=AD=DC
(正方形的四条边都相等,四个角都是直角)
∴∠1+∠2=90°,又∠3+∠2=90°,
∴∠1=∠3
∴△ABM≌△DAN
∴AM=DN
同理 AN=DP
∴AM+AN=DN+DP 即MN=PN.
∴四边形PQMN是正方形
(有一组邻边相等的矩形是正方形)
例题讲解
1、一个正方形的面积等于8,则其对角线的长为 。
2、正方形对角线长6,则它的面积为 ,周长为 。
3、正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于E,则DE的长为 。
A
B
C
D
O
E
4
36
24
2
提示:
∠DAE=∠DEA=67.5°
DE=AD=2
课堂练习
4.如图,已知正方形ABCD,以AB为边向正方形外作等边三角形ABE,连结DE,CE,则∠DEC= 。
A
B
C
D
E
30°
5、如图,已知正方形ABCD内有一个△BEF,AB=6,AF︰FD=1︰2,E为DC的中点,则△BEF的面积= 。
A
B
C
D
F
E
15
课堂练习
6.已知一个四边形是菱形,要使它成为一个正方形,在下列给出的条件中,可添加( )
A.对角线互相平分 B.对角线互相垂直
C.一组邻边相等 D.有一个角是直角
7.下列判断错误的是( )
A.对角线相等的菱形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线互相垂直且相等的平行四边形是正方形
D.对角线互相平分的平行四边形是正方形
D
D
课堂练习
8、已知四边形ABCD,则下列说法中正确的是( )
A.若AB∥CD,AB=CD,则四边形ABCD是平行四边形
B.若AC⊥BD,AC=BD,则四边形ABCD是矩形
C.若AC⊥BD,AB=AD,CB=CD则四边形ABCD是菱形
D.若AB=BC=CD=AD,则四边形ABCD是正方形
A
9、已知一个四边形是矩形,要使它成为一个正方形,在下列给出的条件中,可添加( )
A.对角线互相平分 B.对角线相等
C.一组邻边相等 D.有一个角是直角
C
课堂练习
证明:
∵∠C=90°,DE⊥BC于E,
DF⊥AC于F
∴四边形CEDF是矩形
又∵CD平分∠ACB,
DE⊥BC于E, DF⊥AC于F
∴DE=DF,
矩形CEDF是正方形(一组邻边相等的矩形是正方形)
1、已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
想一想:
你能用另外一种方法完成证明吗?
┓
┓
┓
A
B
C
D
E
F
提升练习
证明:∵CD平分∠ACB,
DE⊥BC于E, DF⊥AC于F
∴DE=DF,
∵∠C=90°
∴∠FCD=∠ECD=45°
∴△ FCD 与△ECD是等腰直角三角形
∴CF=FD=DE=CE
∴四边形CEDF是菱形
∵∠C=90°
∴菱形CEDF是正方形(有一个角是直角的菱形是正方形)
1、已知:如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
一个Rt∠+菱形
┓
┓
┓
A
B
C
D
E
F
提升练习
2 、如图所示,正方形ABCD中,P为BD上一点,PM⊥BC于M, PN⊥DC于N. 试说明:AP=MN
A
B
C
D
P
M
N
证明:
连接PC
∵PM⊥BC , PN⊥DC
四边形ABCD是正方形
∴∠NCM=90°
∴四边形PMCN是矩形
∴PC=MN
又∵四边形BAPC是以BD为轴的轴对称图形
∴AP=PC
∴AP=MN
提升练习
一个角是直角
1.正方形的概念:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
一组邻边相等
平行四边形
矩形
菱形
一组邻边相等
一个角是直角
正方形
有一组邻边相等
有一个角是直角
图示:
课堂小结
课堂小结
2、正方形的性质
课堂小结
四边形
平行四边形
矩形
菱形
正方形
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
3.平行四边形、矩形、菱形、正方形的判定小结
课堂小结
1、已知正方形ABCD, M是AD上的点, ME⊥ BD, MF⊥ AC,垂足分别为E、F
(1) 若对角线AC=12cm, 求ME+MF的长。
A
B
C
D
O
M
F
E
(2)若M是AD上的一个动
点,ME+MF的长度是
否发生改变?
ME + MF = 6cm
课后练习
不改变
2.已知:如图,正方形ABCD的对角线相交于点O,M、N在OB和OC上,且MN∥BC,连结DN、MC,试猜想DN与MC有什么关系?并证明你的猜想。
N
M
O
D
C
B
A
又∵MN∥AB
∴∠OMN=∠1=∠BCO=∠ONM=45° ∴OM=ON
⌒
1
⌒
2
证明:延长DN交MC于H
∵四边形ABCD是正方形
∴OC=OD ,
∠COD=∠COB=90°
∠1=∠BCO=45°
∴△COM≌△DON(SAS)
∴DN=MC
H
⌒
3
答:DN=MC DN⊥MC
∴∠2=∠3
又∠3+∠CMO=90°
∴∠2+∠CMO=90°
∴∠DHM=90°
∴DN⊥MC
课后练习
3、如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两正方形重合部分的面积是多少?
A
B
O
P
Q
R
D
C
E
F
提示:
证△D0E≌△C0F(ASA)
1
第5课时 正方形性质与判定
沪科版数学八年级下册
19.3 矩形、菱形、正方形
教学目标
平行四边形与矩形、菱形有什么联系?
性质
定义
判定
逆向猜想
一个角
是直角
一组邻
边相等
平行四边形
矩形
菱形
知识回顾
研究方法
正方形
正方形
菱形
有一个角是直角
★正方形是特殊的菱形
讨论:
新知探究
A
B
C
D
讨论:
(1)图中CD在平移时,这个图形始终是图形 ;
(2)当CD移动到C D 位置,此时AD =AB,四边形ABCD还是图形 ,是特殊矩形 。
A
B
C
D
★ 正方形是特殊的矩形
两组互相垂直的平行线围成矩形ABCD
矩形
矩形
正方形
新知探究
有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
一、正方形的定义:
_______________的菱形是正方形
_______________的矩形是正方形
由正方形的定义可知:
有一个角是直角
有一组邻边相等
正方形既是菱形,又是矩形
新知讲解
矩形
正方形
有一组邻边相等
各平行四边形关系再认识
平行四边形
菱形
有一组邻边相等
有一个角是直角
有一个角是直角
新知讲解
四边形
平行四边形
矩形
菱形
正方形
从集合的角度看四边形的关系
新知讲解
正方形的性质
正方形即是特殊的矩形又是特殊的菱形。
正方形具有矩形性质,同时也具有菱形形性质。
新知讲解
正方形的边:对边 ,四边_________;
正方形的角:四个角都是________;
正方形的对角线:对角线 ,互相________,互相________每条对角线 平分一组________.
正方形的对称性:是_______________图形.
直角
都相等
平行且相等
轴对称
平分
对角
相等
垂直
填一填
正方形性质1
正方形具有平行四边形、矩形、菱形的一切性质
正方形的四条边都相等,四个角都是直角
正方形性质2
正方形的对角线相等且互相垂直平分
新知讲解
⑵产生了哪些特殊角?
D
O
A
B
C
450
450
450
450
450
450
450
450
4个全等的小等腰直角三角形
900和450
如图,正方形的对角线交于O点
⑴在正方形中产生了哪些特殊图形?
△ABO≌ △BCO ≌ △CDO ≌ △DAO
4个全等的大等腰直角三角形.
△ABC≌ △BCD ≌ △CDA ≌ △DAB
新知讲解
1、正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分
C、对角互补.
D、对角线相等.
2、正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
练习:
随堂练习
3.菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分
B.对角线相等且互相垂直平分
C.对角线互相平分
D.四条边相等,四个角相等
C
随堂练习
正方形的判定
特殊的菱形
特殊的矩形
新知讲解
正方形的判定方法
(可从平行四边形、矩形、菱形为基础)
平行四边形
正方形
一组邻边相等
一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
从边和角看
新知讲解
正方形的判定方法
(可从平行四边形、矩形、菱形为基础)
平行四边形
正方形
对角线相等
对角线垂直
1、
正方形
菱形
2、
对角线相等
矩形
3、
对角线互相垂直
正方形
从对角线看
新知讲解
下列说法对吗
(1)四个角都相等的四边形是正方形( )
(2)四条边都相等的四边形是正方形( )
(3)对角线相等的菱形是正方形( )
(4)对角线互相垂直的矩形是正方形( )
对
错
矩 形
错
菱 形
对
随堂练习
(5)对角线垂直且相等的四边形是正方形( )
(6)四边相等,有一角是直角的四边形是正方形( )
(7) 正方形的一条对角线把正方形分成两个全等的等腰 直角三角形( )
(8) 正方形是轴对称图形,一共有2条对称轴( )
下列说法对吗
错
对
对
错
4条对称轴
随堂练习
例1· AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:EC=EF=FB
A
B
C
D
E
F
┌
证明: ∵ 四边形ABCD是正方形
∴∠B=900 ∠ACB=450
∵∠AEF=900 AB=AE
∴△ABF≌△AFE(HL)
∴BF=EF
又∵∠FEC=900
∴∠EFC=450
∴EC=EF(等角对等边)
∴BF=EF=EC
例题讲解
已知2:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
A
B
C
D
E
G
┌
F
O
证明:
∵ 四边形ABCD是正方形,
∴ ∠AOE=∠DOF=90°,AO=DO
(正方形的对角线垂直平分且相等).
∵ DG⊥AE,
∴ ∠EAO+∠AEO=∠EDG+∠AEO=90°.
∴ ∠EAO=∠FDO.
∴ △AEO ≌△DFO.(ASA)
∴ OE=OF.
例题讲解
例3、已知:如图,四边形ABCD是正方形,分别过点A、C两点l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点
求证:四边形PQMN是正方形.
A
B
C
D
Q
M
N
P
l1
l2
3
2
1
证明:∵PN⊥l1,QM⊥l1,
∴PN∥QM,∠PNM=90°
∵PQ∥NM,∴四边形PQMN是矩形
∵四边形ABCD是正方形
∴∠BAD=∠ADC=90°,AB=AD=DC
(正方形的四条边都相等,四个角都是直角)
∴∠1+∠2=90°,又∠3+∠2=90°,
∴∠1=∠3
∴△ABM≌△DAN
∴AM=DN
同理 AN=DP
∴AM+AN=DN+DP 即MN=PN.
∴四边形PQMN是正方形
(有一组邻边相等的矩形是正方形)
例题讲解
1、一个正方形的面积等于8,则其对角线的长为 。
2、正方形对角线长6,则它的面积为 ,周长为 。
3、正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于E,则DE的长为 。
A
B
C
D
O
E
4
36
24
2
提示:
∠DAE=∠DEA=67.5°
DE=AD=2
课堂练习
4.如图,已知正方形ABCD,以AB为边向正方形外作等边三角形ABE,连结DE,CE,则∠DEC= 。
A
B
C
D
E
30°
5、如图,已知正方形ABCD内有一个△BEF,AB=6,AF︰FD=1︰2,E为DC的中点,则△BEF的面积= 。
A
B
C
D
F
E
15
课堂练习
6.已知一个四边形是菱形,要使它成为一个正方形,在下列给出的条件中,可添加( )
A.对角线互相平分 B.对角线互相垂直
C.一组邻边相等 D.有一个角是直角
7.下列判断错误的是( )
A.对角线相等的菱形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线互相垂直且相等的平行四边形是正方形
D.对角线互相平分的平行四边形是正方形
D
D
课堂练习
8、已知四边形ABCD,则下列说法中正确的是( )
A.若AB∥CD,AB=CD,则四边形ABCD是平行四边形
B.若AC⊥BD,AC=BD,则四边形ABCD是矩形
C.若AC⊥BD,AB=AD,CB=CD则四边形ABCD是菱形
D.若AB=BC=CD=AD,则四边形ABCD是正方形
A
9、已知一个四边形是矩形,要使它成为一个正方形,在下列给出的条件中,可添加( )
A.对角线互相平分 B.对角线相等
C.一组邻边相等 D.有一个角是直角
C
课堂练习
证明:
∵∠C=90°,DE⊥BC于E,
DF⊥AC于F
∴四边形CEDF是矩形
又∵CD平分∠ACB,
DE⊥BC于E, DF⊥AC于F
∴DE=DF,
矩形CEDF是正方形(一组邻边相等的矩形是正方形)
1、已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
想一想:
你能用另外一种方法完成证明吗?
┓
┓
┓
A
B
C
D
E
F
提升练习
证明:∵CD平分∠ACB,
DE⊥BC于E, DF⊥AC于F
∴DE=DF,
∵∠C=90°
∴∠FCD=∠ECD=45°
∴△ FCD 与△ECD是等腰直角三角形
∴CF=FD=DE=CE
∴四边形CEDF是菱形
∵∠C=90°
∴菱形CEDF是正方形(有一个角是直角的菱形是正方形)
1、已知:如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
一个Rt∠+菱形
┓
┓
┓
A
B
C
D
E
F
提升练习
2 、如图所示,正方形ABCD中,P为BD上一点,PM⊥BC于M, PN⊥DC于N. 试说明:AP=MN
A
B
C
D
P
M
N
证明:
连接PC
∵PM⊥BC , PN⊥DC
四边形ABCD是正方形
∴∠NCM=90°
∴四边形PMCN是矩形
∴PC=MN
又∵四边形BAPC是以BD为轴的轴对称图形
∴AP=PC
∴AP=MN
提升练习
一个角是直角
1.正方形的概念:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
一组邻边相等
平行四边形
矩形
菱形
一组邻边相等
一个角是直角
正方形
有一组邻边相等
有一个角是直角
图示:
课堂小结
课堂小结
2、正方形的性质
课堂小结
四边形
平行四边形
矩形
菱形
正方形
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
3.平行四边形、矩形、菱形、正方形的判定小结
课堂小结
1、已知正方形ABCD, M是AD上的点, ME⊥ BD, MF⊥ AC,垂足分别为E、F
(1) 若对角线AC=12cm, 求ME+MF的长。
A
B
C
D
O
M
F
E
(2)若M是AD上的一个动
点,ME+MF的长度是
否发生改变?
ME + MF = 6cm
课后练习
不改变
2.已知:如图,正方形ABCD的对角线相交于点O,M、N在OB和OC上,且MN∥BC,连结DN、MC,试猜想DN与MC有什么关系?并证明你的猜想。
N
M
O
D
C
B
A
又∵MN∥AB
∴∠OMN=∠1=∠BCO=∠ONM=45° ∴OM=ON
⌒
1
⌒
2
证明:延长DN交MC于H
∵四边形ABCD是正方形
∴OC=OD ,
∠COD=∠COB=90°
∠1=∠BCO=45°
∴△COM≌△DON(SAS)
∴DN=MC
H
⌒
3
答:DN=MC DN⊥MC
∴∠2=∠3
又∠3+∠CMO=90°
∴∠2+∠CMO=90°
∴∠DHM=90°
∴DN⊥MC
课后练习
3、如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两正方形重合部分的面积是多少?
A
B
O
P
Q
R
D
C
E
F
提示:
证△D0E≌△C0F(ASA)
1
