西南师大版六年级数学下册三 正比例和反比例《反比例》教案
文档属性
| 名称 | 西南师大版六年级数学下册三 正比例和反比例《反比例》教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 504.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-27 00:00:00 | ||
图片预览




文档简介
《反比例的意义》教学设计
教学内容:教科书48页例1.
例题呈现:
内容理解:这部分内容是在学生已经学习了比和比例以及正比例的意义的基础上进行教学的。通过教学使学生结合实际情境认识成反比例的量,能根据反比例的意义判断两种相关联的量是否成反比例;使学生在认识成反比例的量过程中,进一步体会数量之间相依互变的关系,感受有效表示数量关系及其变化的不同数学模型,提升思维水平;体会数学与日常生活的密切联系,增强探索数学知识和规律的意识。
教材编写意图:
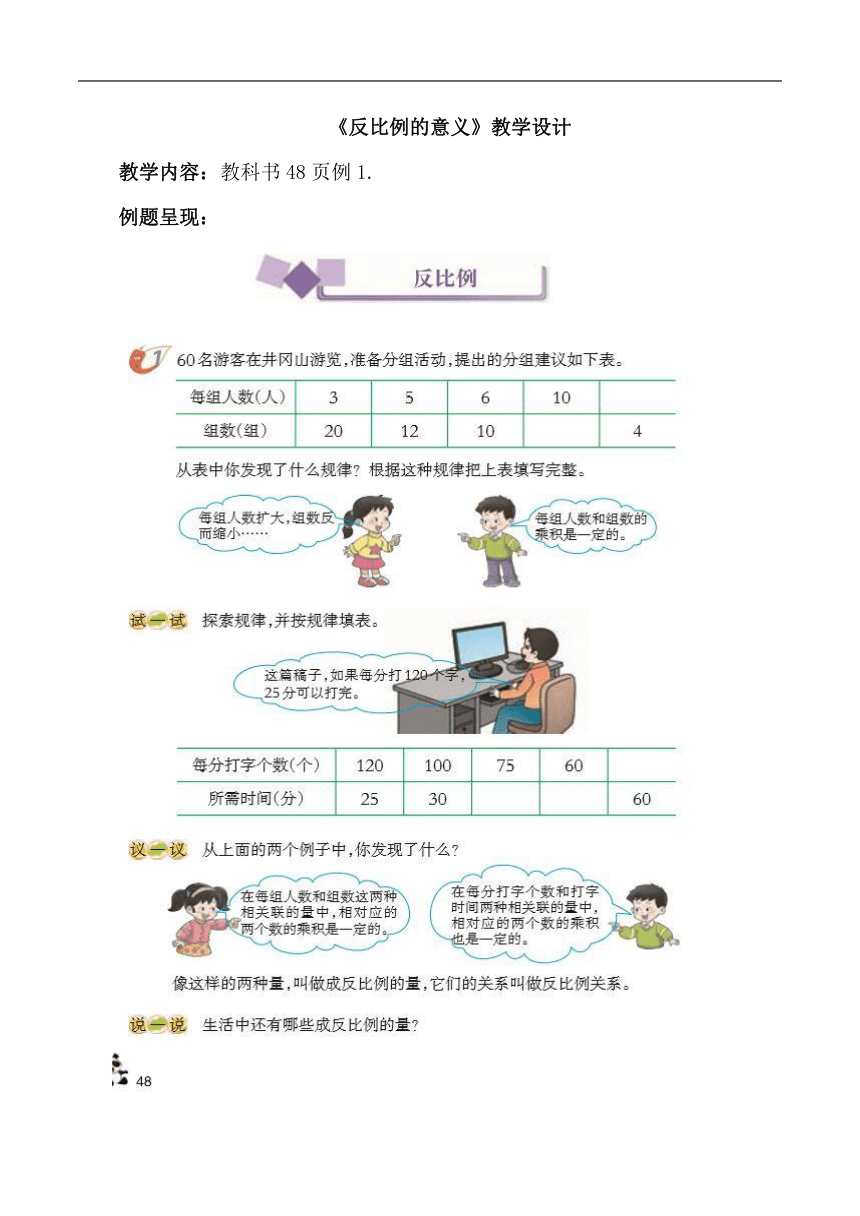
(1)以60名游客在井冈山游览时如何分组的情境引入。
(2)利用表格呈现每组人数和组数的变化情况,观察发现其变化的规律和不变的量。
(3)再列举:每分打字个数和所需时间的变化情况,观察发现其变化的规律和不变的量。
(4)利用“议一议”,讨论得出反比例的意义。
(5)“说一说”,让学生举例说出生活中成反比例的量。
数学思考:
(1)学生在认识反比例的过程中,进一步体会数量之间相依互变的关系,渗透函数思想。
(2)感受有效表示数量关系及其变化的不同数学模型,提升思维水平。
(3)体会数学与日常生活的联系,增强探索数学知识和规律的意识。
教学设想:通过实际情境呈现出呈反比例关系的量,让学生发现其变化的规律,认识反比例的意义;引导学生概括出判断两个量是否成反比例的方法;比较正、反比例这两种表示数量关系变化的数学模型的异同,从而使学生更加准确、熟练地判断正、反比例关系,提升数学思维水平,让学生列举生活中成反比例关系的量,体会数学与生活的密切联系,增强探索生活中数学知识和规律的意识。
教学目标:
1、在现实情境中认识反比例,会判断两个相关联的量是否成反比例关系。
2、进一步体会生活中数量之间相依互变的关系,通过观察、分析其变化规律,建立数学模型,提升数学思维水平。
3、体会数学与生活的密切联系,增强探索生活中数学知识和规律的意识。
教学重、难点:
认识反比例的意义,正确判断两个相关联的量是否成反比例。
教学过程:
课前交流:(略)
1、 情境引入、复习回顾
师:同学们!你们知道世界上最快的汽车能跑多快吗?大胆猜一下!
生:200km/h,300km/h,500km/h……
师:(出示图片)介绍资料!如果速度按3000km/h计算,你能计算填写这个表格吗?(出示表格)快速计算!
资料:音速之风陆地极速车 (最高时速:3218千米)
美国承包商瓦尔多 斯塔克斯使用航天器及核弹零部件制造了一辆高速汽车,名为“音速之风陆地极速车”,最高时速可达到令人吃惊的2000英里(约合每小时3218公里)
速度按3000km/h计算:
时间(h) 1 2 4 6 10
路程(km) 3000 6000 12000 18000 30000
师:观察表格中,有哪两种相关联的量?它们是什么关系?为什么?
生:(两种相关联的量是路程和时间,它们是正比例关系,因为路程随时间的增大而增大(或者说出路程和时间准确的变化规律);路程和时间的比值是一定的。)
师:(根据学生回答板书;正比例;两个相关联的量;变化;比值一定)
师:你能结合表格用一句完整的话说一说什么样的两个量是成正比例关系的?
生:(两个相关联的量,如果一个量增大,另一个量也随之增大,且它们的比值是一定的,那么……)
师:在这里,路程和时间的比值表示什么意义?你能用一个数量关系式表示出来吗?
生:比值就是速度(3000km/h一定),关系式可以表示为:路程/时间=速度(一定)
师:由这个关系式,我们可以说:速度一定,路程和时间成……(正比例关系)
2、变换情境、揭示课题
师:接下来,让我们再来看一个事例!(出示情境:文字)
师:60名游客在井冈山游览,准备分组活动,你认为有几种分组方案?
生:(分为2组,每组30人;分为3组,每组20人……)
师:综合刚才同学们说的方案,我们将其整理成表格:(出示表格)
每组人数(人) 3 5 6 10 15
组数(组) 20 12 10 6 4
师:观察表格中有哪两种相关联的量?观察这两种相关联的量,你发现了什么规律?
生:(两种相关联的量是组数和每组人数;每组人数增大,组数反而变小;每组人数和组数的乘积不变)(师:板书:两种相关联的量;变化;乘积一定)
师:这两个相关联的量是成正比例的吗?为什么?
生:(不是成正比例的,因为它们不是比值一 定,而是乘积是一定的)
师:像这样的两种量不是成正比例关系的,那它们是什么关系呢?
生:(反比例)师:(板书:课题:反比例)
师:这节课我们就来研究反比例,那么我们要研究反比例的哪些问题呢?
生:(什么是反比例?怎样判断两个量是不是成反比例的?……)师:(板书:意义;判断;异同;生活;应用……)
3、自主学习,释疑、建模。
师:为了更好地认识反比例,接下来,我们再来看一个事例。(课件展示:图片、文字)
师:云图框中:这篇稿子,如果每分钟打120个字,25分钟可以打完。我们可以从这句话中得到什么信息?你能找到规律,并将表格填写完整吗?
每分打字个数(个) 120 100 75 60 50
所需时间(分) 25 30 40 50 60
生:(汇报题意的理解,填写表格的情况)
师:观察表格:有哪两种相关联的量?它们成什么关系?为什么?把你的想法在同桌两人小组中交流一下!
生:(汇报)
师:(课件展示:两个表格合在一张幻灯片上)
通过对这两个表格的观察和研究,你能说一说什么是反比例吗?
生:(可以请2-3名学生汇报)
师:(可以结合板书内容引导学生一起来说一遍:两个相关联的量,一个量随另一个量的变化而变化,且它们的乘积一定,这两个量就是……)
师:表格一中,两个量的乘积是表示什么意义?我们可以用一个关系式来表达吗?
生:(两个量的乘积是游客总人数,关系式为:每组人数×组数=总人数(一定))
师:(板书关系式)由关系式,我们可以说,总人数一定,每组人数和组数成……(反比例关系)
师:表二呢?
生:(汇报!)(师生可以一起说一遍:总字数一定……)
师:如果用字母x、y来表示这两个量,它们的关系式可以表示为:
xy=k(一定)
4、联系实际,融汇理解
师:那么,生活中还有哪些成反比例的量呢?你能举例说一说吗?一分钟时间和你的同桌说一说!(再抽学生回答)生:汇报!
5、课堂活动、合作探究
活动一:师:接下来,我们通过两个课堂活动来加深一下对反比例的认识和理解!同桌两人小组可以合作完成!填写表格,并思考回答表格下的问题!
生:(展台汇报)师:表格中长和宽的乘积是什么?用数量关系式可以表示为?(板书:长×宽=长方形的面积(一定))
师:我们可以说长方形的面积一定,长和宽成……(反比例关系)
活动二
6、数形结合,升华应用
一根水管不停地向水箱注水,箱的水量变化情况如图一所示;一项工作,工作人数和工作时间的关系如图二所示:
师:你能判断关系图中的两个量是什么关系吗?你是怎样判断的呢?
生:(汇报)
师:老师这里也准备了一些例子需要同学们来帮着判断一下!(出示内容)
判断下面各题中的两种量是否成反比例关系?为什么?
1、一筐桃子平均分给猴子,猴的只数和每只猴分桃的个数。2、圆柱的体积一定,它的底面积和高。3、工作总量一定,工作效率和工作时间。4、互为倒数的两个数。5、报纸的单价一定,订阅的份数与总价。6、小明看一本书,已看的页数和没有看的页数。
师:现在你能比较正、反比例的异同了吗?哪里表现了“正”“反”两个字的区别?
生:(学生根据板书内容容易比较并描述正、反比例的异同)
师:我们还可以用一个童谣来比较正、反比例:(学生齐读)
正反比例两兄弟,样子相像性格异。
正比例,很和气;你扩大,他扩大,倍数相同顺着你。
反比例,倔脾气;你扩大,他缩小,倍数相同顶撞你。
7、小结:这节课你学会了什么?还有哪些疑惑?
师:生活中有许多成正、反比例的量,还有很多比正、反比例更有趣也更复杂的变与不变的关系,只要我们留心观察、用心思考,就会发现我们生活中有很多的数学知识等待着我们去探索、去发现!
附板书设计:(略)
教学内容:教科书48页例1.
例题呈现:
内容理解:这部分内容是在学生已经学习了比和比例以及正比例的意义的基础上进行教学的。通过教学使学生结合实际情境认识成反比例的量,能根据反比例的意义判断两种相关联的量是否成反比例;使学生在认识成反比例的量过程中,进一步体会数量之间相依互变的关系,感受有效表示数量关系及其变化的不同数学模型,提升思维水平;体会数学与日常生活的密切联系,增强探索数学知识和规律的意识。
教材编写意图:
(1)以60名游客在井冈山游览时如何分组的情境引入。
(2)利用表格呈现每组人数和组数的变化情况,观察发现其变化的规律和不变的量。
(3)再列举:每分打字个数和所需时间的变化情况,观察发现其变化的规律和不变的量。
(4)利用“议一议”,讨论得出反比例的意义。
(5)“说一说”,让学生举例说出生活中成反比例的量。
数学思考:
(1)学生在认识反比例的过程中,进一步体会数量之间相依互变的关系,渗透函数思想。
(2)感受有效表示数量关系及其变化的不同数学模型,提升思维水平。
(3)体会数学与日常生活的联系,增强探索数学知识和规律的意识。
教学设想:通过实际情境呈现出呈反比例关系的量,让学生发现其变化的规律,认识反比例的意义;引导学生概括出判断两个量是否成反比例的方法;比较正、反比例这两种表示数量关系变化的数学模型的异同,从而使学生更加准确、熟练地判断正、反比例关系,提升数学思维水平,让学生列举生活中成反比例关系的量,体会数学与生活的密切联系,增强探索生活中数学知识和规律的意识。
教学目标:
1、在现实情境中认识反比例,会判断两个相关联的量是否成反比例关系。
2、进一步体会生活中数量之间相依互变的关系,通过观察、分析其变化规律,建立数学模型,提升数学思维水平。
3、体会数学与生活的密切联系,增强探索生活中数学知识和规律的意识。
教学重、难点:
认识反比例的意义,正确判断两个相关联的量是否成反比例。
教学过程:
课前交流:(略)
1、 情境引入、复习回顾
师:同学们!你们知道世界上最快的汽车能跑多快吗?大胆猜一下!
生:200km/h,300km/h,500km/h……
师:(出示图片)介绍资料!如果速度按3000km/h计算,你能计算填写这个表格吗?(出示表格)快速计算!
资料:音速之风陆地极速车 (最高时速:3218千米)
美国承包商瓦尔多 斯塔克斯使用航天器及核弹零部件制造了一辆高速汽车,名为“音速之风陆地极速车”,最高时速可达到令人吃惊的2000英里(约合每小时3218公里)
速度按3000km/h计算:
时间(h) 1 2 4 6 10
路程(km) 3000 6000 12000 18000 30000
师:观察表格中,有哪两种相关联的量?它们是什么关系?为什么?
生:(两种相关联的量是路程和时间,它们是正比例关系,因为路程随时间的增大而增大(或者说出路程和时间准确的变化规律);路程和时间的比值是一定的。)
师:(根据学生回答板书;正比例;两个相关联的量;变化;比值一定)
师:你能结合表格用一句完整的话说一说什么样的两个量是成正比例关系的?
生:(两个相关联的量,如果一个量增大,另一个量也随之增大,且它们的比值是一定的,那么……)
师:在这里,路程和时间的比值表示什么意义?你能用一个数量关系式表示出来吗?
生:比值就是速度(3000km/h一定),关系式可以表示为:路程/时间=速度(一定)
师:由这个关系式,我们可以说:速度一定,路程和时间成……(正比例关系)
2、变换情境、揭示课题
师:接下来,让我们再来看一个事例!(出示情境:文字)
师:60名游客在井冈山游览,准备分组活动,你认为有几种分组方案?
生:(分为2组,每组30人;分为3组,每组20人……)
师:综合刚才同学们说的方案,我们将其整理成表格:(出示表格)
每组人数(人) 3 5 6 10 15
组数(组) 20 12 10 6 4
师:观察表格中有哪两种相关联的量?观察这两种相关联的量,你发现了什么规律?
生:(两种相关联的量是组数和每组人数;每组人数增大,组数反而变小;每组人数和组数的乘积不变)(师:板书:两种相关联的量;变化;乘积一定)
师:这两个相关联的量是成正比例的吗?为什么?
生:(不是成正比例的,因为它们不是比值一 定,而是乘积是一定的)
师:像这样的两种量不是成正比例关系的,那它们是什么关系呢?
生:(反比例)师:(板书:课题:反比例)
师:这节课我们就来研究反比例,那么我们要研究反比例的哪些问题呢?
生:(什么是反比例?怎样判断两个量是不是成反比例的?……)师:(板书:意义;判断;异同;生活;应用……)
3、自主学习,释疑、建模。
师:为了更好地认识反比例,接下来,我们再来看一个事例。(课件展示:图片、文字)
师:云图框中:这篇稿子,如果每分钟打120个字,25分钟可以打完。我们可以从这句话中得到什么信息?你能找到规律,并将表格填写完整吗?
每分打字个数(个) 120 100 75 60 50
所需时间(分) 25 30 40 50 60
生:(汇报题意的理解,填写表格的情况)
师:观察表格:有哪两种相关联的量?它们成什么关系?为什么?把你的想法在同桌两人小组中交流一下!
生:(汇报)
师:(课件展示:两个表格合在一张幻灯片上)
通过对这两个表格的观察和研究,你能说一说什么是反比例吗?
生:(可以请2-3名学生汇报)
师:(可以结合板书内容引导学生一起来说一遍:两个相关联的量,一个量随另一个量的变化而变化,且它们的乘积一定,这两个量就是……)
师:表格一中,两个量的乘积是表示什么意义?我们可以用一个关系式来表达吗?
生:(两个量的乘积是游客总人数,关系式为:每组人数×组数=总人数(一定))
师:(板书关系式)由关系式,我们可以说,总人数一定,每组人数和组数成……(反比例关系)
师:表二呢?
生:(汇报!)(师生可以一起说一遍:总字数一定……)
师:如果用字母x、y来表示这两个量,它们的关系式可以表示为:
xy=k(一定)
4、联系实际,融汇理解
师:那么,生活中还有哪些成反比例的量呢?你能举例说一说吗?一分钟时间和你的同桌说一说!(再抽学生回答)生:汇报!
5、课堂活动、合作探究
活动一:师:接下来,我们通过两个课堂活动来加深一下对反比例的认识和理解!同桌两人小组可以合作完成!填写表格,并思考回答表格下的问题!
生:(展台汇报)师:表格中长和宽的乘积是什么?用数量关系式可以表示为?(板书:长×宽=长方形的面积(一定))
师:我们可以说长方形的面积一定,长和宽成……(反比例关系)
活动二
6、数形结合,升华应用
一根水管不停地向水箱注水,箱的水量变化情况如图一所示;一项工作,工作人数和工作时间的关系如图二所示:
师:你能判断关系图中的两个量是什么关系吗?你是怎样判断的呢?
生:(汇报)
师:老师这里也准备了一些例子需要同学们来帮着判断一下!(出示内容)
判断下面各题中的两种量是否成反比例关系?为什么?
1、一筐桃子平均分给猴子,猴的只数和每只猴分桃的个数。2、圆柱的体积一定,它的底面积和高。3、工作总量一定,工作效率和工作时间。4、互为倒数的两个数。5、报纸的单价一定,订阅的份数与总价。6、小明看一本书,已看的页数和没有看的页数。
师:现在你能比较正、反比例的异同了吗?哪里表现了“正”“反”两个字的区别?
生:(学生根据板书内容容易比较并描述正、反比例的异同)
师:我们还可以用一个童谣来比较正、反比例:(学生齐读)
正反比例两兄弟,样子相像性格异。
正比例,很和气;你扩大,他扩大,倍数相同顺着你。
反比例,倔脾气;你扩大,他缩小,倍数相同顶撞你。
7、小结:这节课你学会了什么?还有哪些疑惑?
师:生活中有许多成正、反比例的量,还有很多比正、反比例更有趣也更复杂的变与不变的关系,只要我们留心观察、用心思考,就会发现我们生活中有很多的数学知识等待着我们去探索、去发现!
附板书设计:(略)
