青岛版七年级数学下册 9.4 平行线的判定课件(共18张PPT)
文档属性
| 名称 | 青岛版七年级数学下册 9.4 平行线的判定课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 736.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 07:07:53 | ||
图片预览




文档简介
(共19张PPT)
9.4 平行线的判定
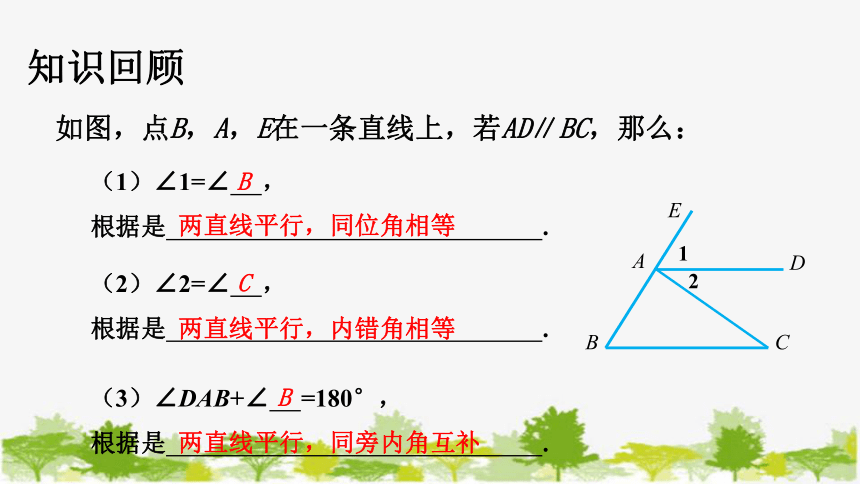
如图,点B,A,E在一条直线上,若AD∥BC,那么:
(1)∠1=∠ ,
根据是 .
(2)∠2=∠ ,
根据是 .
(3)∠DAB+∠ =180°,
根据是 .
E
C
D
B
A
1
2
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
B
C
B
知识回顾
一、放
二、靠
三、推
四、画
平行线的画法
1.经历实验操作、观察、推理、思考、交流等活动,探索平行线的三个判定方法。
2.记住平行线的三个判定方法,并会用它们判定两直线平行。
3.通过活动培养推理意识和语言表达能力。
学习目标
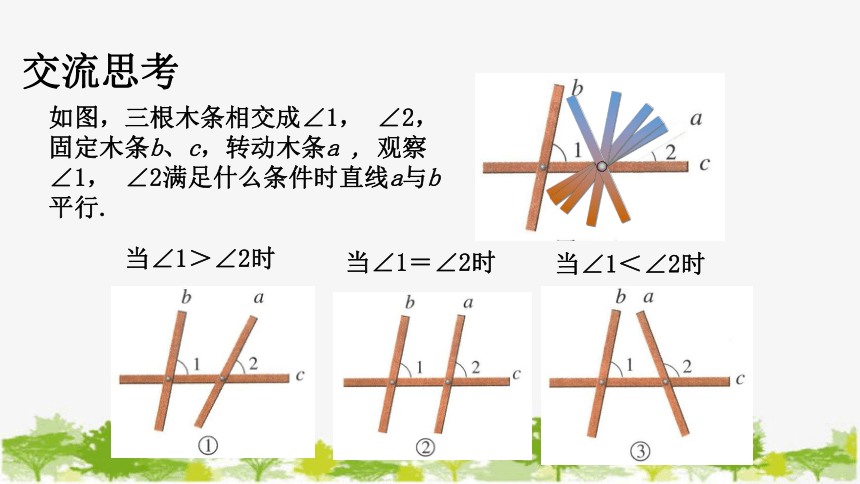
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
交流思考
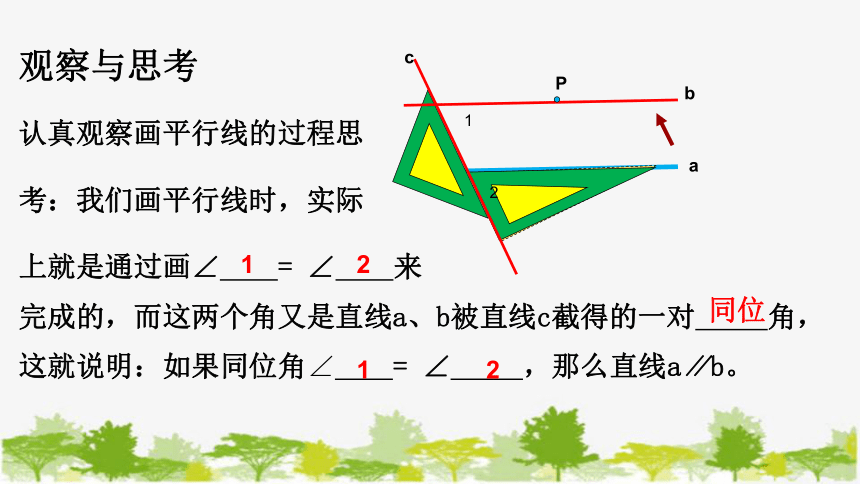
观察与思考
认真观察画平行线的过程思
考:我们画平行线时,实际
上就是通过画∠ = ∠ 来
完成的,而这两个角又是直线a、b被直线c截得的一对 角,这就说明:如果同位角∠ = ∠ ,那么直线a∥b。
a
b
P
1
2
c
1
2
同位
1
2
两直线平行的判定方法1
你能用自己的语言叙述上面的结论吗?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
符号语言:
因为∠1=∠2,(已知)
所以 a∥b.(同位角相等,两直线平行)
交流与发现
如图,∠1= ∠2,直线a与直线b平行吗?为什么?
1
2
3
a
b
c
解:a ∥b.
因为∠1=∠2, (已知)
∠1 =∠3,(对顶角相等)
所以 ∠2=∠3,(等量代换)
所以 a∥b.(同位角相等,两直线平行)
1
2
a
b
两条直线被第三条直线所截,如果 相等,那么两条直线平行.
内错角
两直线平行的判定方法2
通过上面的题目可以得到:
c
如图 ,几何语言:
因为∠1=∠2(已知)
所以a∥b(内错角相等,两直线平行)
如图,∠1与∠2互补,直线a与直线b平行吗?为什么?与其他同学交流。
解:a∥b.
因为 ∠1与∠2互补,
所以 ∠1+∠2=180°,(补角定义) ∠2+∠3 =180°,(平角定义)
所以 ∠1=∠3,(同角的补角相等 )
所以 a∥b.(同位角相等,两直线平行)
1
2
3
a
c
b
交流与发现
两条直线被第三条直线所截,如果 互补,那么两条直线平行.
通过上面的题目可以得到:
同旁内角
1
2
a
c
b
两直线平行的判定方法2
如图,几何语言:
因为∠1+∠2=180 °(已知)
所以a∥b(同旁内角互补,两直线平行)
1、如图,下列条件中,不能判断直线l1∥l2 的是( )
A.∠1=∠3 B.∠2=∠3
C.∠4=∠5 D.∠2+∠4=180°
2、如图,AC ⊥AE,BD ⊥BF,∠1=28°,
∠2=28°,试说明:AC∥BD ,AE∥BF.
解:因为∠1=28°,∠2=28°,
所以∠1=∠2,所以AC∥BD .
因为AC⊥AE,BD ⊥BF,所以∠EAC=∠FBD =90°.
所以∠EAC+∠1=∠FBD +∠2,
即∠EAB=∠FBG.所以AE∥BF.
B
已知:如图,a⊥c,b⊥c.试说明:a∥b.
1
2
a
b
c
结论:在同一平面内,垂直于同一条直线的两
条直线互平行。
思考
同旁内角互补,两直线平行。
画平行线的事实
同位角相等, 两直线平行。
内错角相等,
两直线平行。
小结
平行线的判定方法
判定
方法 文字语言
简称
几何语言
图示
方法1 两条直线被第三条直线
所截,如果同位角相等,
那么这两条直线平行 同位角相等,
两直线平行 因为1=∠2,
所以l1∥l2
方法2 两条直线被第三条直线
所截,如果内错角相等,
那么这两条直线平行 内错角相等,
两直线平行 因为∠2=∠3,
所以l1∥l2
方法3 两条直线被第三条直线
所截,如果同旁内角互
补,那么这两条直线平行 同旁内角互补,
两直线平行 因为∠2+∠4=180°,
所以l1∥l2
D
1、如图,能判定EB∥AC 的条件是( )
A.∠C=∠ABE B.∠A =∠EBD
C.∠C=∠ABC D.∠A =∠ABE
2、如图,∠1=40°,下面结论正确的有( )
①若∠2=40°,则AB∥CD ;
②若∠5=40°,则AB∥CD ;
③若∠3=140°,则AB∥CD ;
④若∠4=140°,则AB∥CD .
A.1个 B.2个 C.3个 D.4个
B
巩固练习
3、如图,∠BAF =38°,DC ⊥CE,∠ACE =128°.
试判断AB 与DC 的位置关系,并说明理由.
解:AB∥DC.理由如下:
因为∠BAF=38°,∠BAF+∠CAB=180°,
所以∠CAB=142°.
因为DC⊥CE,所以∠DCE=90°.
又因为∠DCE + ∠ACE + ∠DCA =360°,
∠ACE=128°,所以∠DCA =142°.
所以∠DCA =∠CAB.所以AB∥DC.
4、如图,点E 在直线DF上,点B 在直线AC 上.若∠AGB = ∠EHF,∠C =∠D ,试判断∠A 与∠F 的关系,并说明理由.
解:∠A =∠F.理由如下:
因为∠AGB=∠DGF,∠AGB=∠EHF,
所以∠DGF=∠EHF.所以BD ∥CE.
所以∠C=∠ABD .
又因为∠C=∠D ,所以∠D =∠ABD .
所以DF∥AC.所以∠A =∠F.
9.4 平行线的判定
如图,点B,A,E在一条直线上,若AD∥BC,那么:
(1)∠1=∠ ,
根据是 .
(2)∠2=∠ ,
根据是 .
(3)∠DAB+∠ =180°,
根据是 .
E
C
D
B
A
1
2
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
B
C
B
知识回顾
一、放
二、靠
三、推
四、画
平行线的画法
1.经历实验操作、观察、推理、思考、交流等活动,探索平行线的三个判定方法。
2.记住平行线的三个判定方法,并会用它们判定两直线平行。
3.通过活动培养推理意识和语言表达能力。
学习目标
如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
交流思考
观察与思考
认真观察画平行线的过程思
考:我们画平行线时,实际
上就是通过画∠ = ∠ 来
完成的,而这两个角又是直线a、b被直线c截得的一对 角,这就说明:如果同位角∠ = ∠ ,那么直线a∥b。
a
b
P
1
2
c
1
2
同位
1
2
两直线平行的判定方法1
你能用自己的语言叙述上面的结论吗?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
符号语言:
因为∠1=∠2,(已知)
所以 a∥b.(同位角相等,两直线平行)
交流与发现
如图,∠1= ∠2,直线a与直线b平行吗?为什么?
1
2
3
a
b
c
解:a ∥b.
因为∠1=∠2, (已知)
∠1 =∠3,(对顶角相等)
所以 ∠2=∠3,(等量代换)
所以 a∥b.(同位角相等,两直线平行)
1
2
a
b
两条直线被第三条直线所截,如果 相等,那么两条直线平行.
内错角
两直线平行的判定方法2
通过上面的题目可以得到:
c
如图 ,几何语言:
因为∠1=∠2(已知)
所以a∥b(内错角相等,两直线平行)
如图,∠1与∠2互补,直线a与直线b平行吗?为什么?与其他同学交流。
解:a∥b.
因为 ∠1与∠2互补,
所以 ∠1+∠2=180°,(补角定义) ∠2+∠3 =180°,(平角定义)
所以 ∠1=∠3,(同角的补角相等 )
所以 a∥b.(同位角相等,两直线平行)
1
2
3
a
c
b
交流与发现
两条直线被第三条直线所截,如果 互补,那么两条直线平行.
通过上面的题目可以得到:
同旁内角
1
2
a
c
b
两直线平行的判定方法2
如图,几何语言:
因为∠1+∠2=180 °(已知)
所以a∥b(同旁内角互补,两直线平行)
1、如图,下列条件中,不能判断直线l1∥l2 的是( )
A.∠1=∠3 B.∠2=∠3
C.∠4=∠5 D.∠2+∠4=180°
2、如图,AC ⊥AE,BD ⊥BF,∠1=28°,
∠2=28°,试说明:AC∥BD ,AE∥BF.
解:因为∠1=28°,∠2=28°,
所以∠1=∠2,所以AC∥BD .
因为AC⊥AE,BD ⊥BF,所以∠EAC=∠FBD =90°.
所以∠EAC+∠1=∠FBD +∠2,
即∠EAB=∠FBG.所以AE∥BF.
B
已知:如图,a⊥c,b⊥c.试说明:a∥b.
1
2
a
b
c
结论:在同一平面内,垂直于同一条直线的两
条直线互平行。
思考
同旁内角互补,两直线平行。
画平行线的事实
同位角相等, 两直线平行。
内错角相等,
两直线平行。
小结
平行线的判定方法
判定
方法 文字语言
简称
几何语言
图示
方法1 两条直线被第三条直线
所截,如果同位角相等,
那么这两条直线平行 同位角相等,
两直线平行 因为1=∠2,
所以l1∥l2
方法2 两条直线被第三条直线
所截,如果内错角相等,
那么这两条直线平行 内错角相等,
两直线平行 因为∠2=∠3,
所以l1∥l2
方法3 两条直线被第三条直线
所截,如果同旁内角互
补,那么这两条直线平行 同旁内角互补,
两直线平行 因为∠2+∠4=180°,
所以l1∥l2
D
1、如图,能判定EB∥AC 的条件是( )
A.∠C=∠ABE B.∠A =∠EBD
C.∠C=∠ABC D.∠A =∠ABE
2、如图,∠1=40°,下面结论正确的有( )
①若∠2=40°,则AB∥CD ;
②若∠5=40°,则AB∥CD ;
③若∠3=140°,则AB∥CD ;
④若∠4=140°,则AB∥CD .
A.1个 B.2个 C.3个 D.4个
B
巩固练习
3、如图,∠BAF =38°,DC ⊥CE,∠ACE =128°.
试判断AB 与DC 的位置关系,并说明理由.
解:AB∥DC.理由如下:
因为∠BAF=38°,∠BAF+∠CAB=180°,
所以∠CAB=142°.
因为DC⊥CE,所以∠DCE=90°.
又因为∠DCE + ∠ACE + ∠DCA =360°,
∠ACE=128°,所以∠DCA =142°.
所以∠DCA =∠CAB.所以AB∥DC.
4、如图,点E 在直线DF上,点B 在直线AC 上.若∠AGB = ∠EHF,∠C =∠D ,试判断∠A 与∠F 的关系,并说明理由.
解:∠A =∠F.理由如下:
因为∠AGB=∠DGF,∠AGB=∠EHF,
所以∠DGF=∠EHF.所以BD ∥CE.
所以∠C=∠ABD .
又因为∠C=∠D ,所以∠D =∠ABD .
所以DF∥AC.所以∠A =∠F.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
