小学数学苏教版六年级下7.2.2 平面图形的认识 课件(共17张PPT)
文档属性
| 名称 | 小学数学苏教版六年级下7.2.2 平面图形的认识 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 839.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-28 07:12:09 | ||
图片预览


文档简介
(共17张PPT)
名称 端点数量 能否度量
直线 无 否
射线 一个 否
线段 两个 能
1. 直线、射线、线段的比较
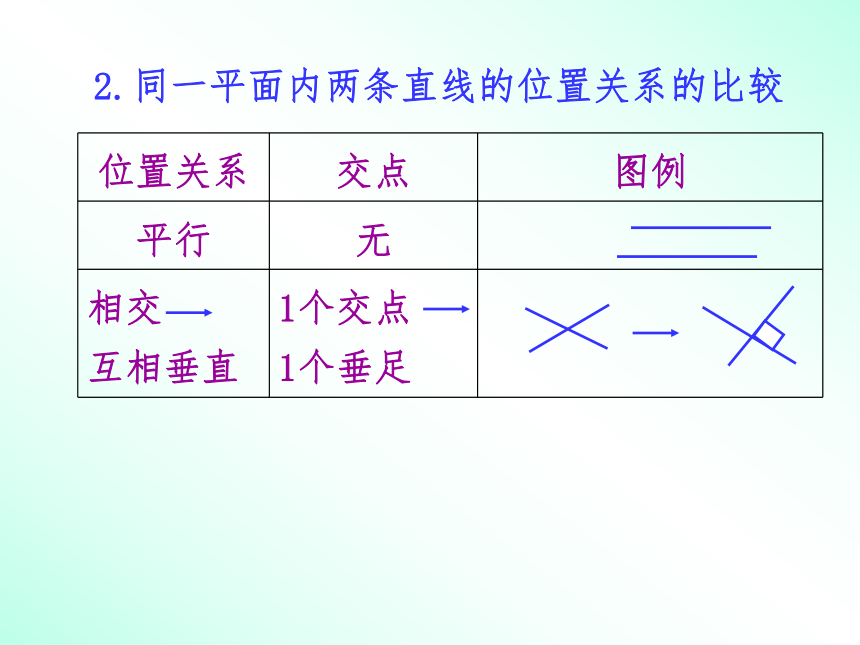
2.同一平面内两条直线的位置关系的比较
位置关系 交点 图例
平行 无
相交
互相垂直 1个交点
1个垂足
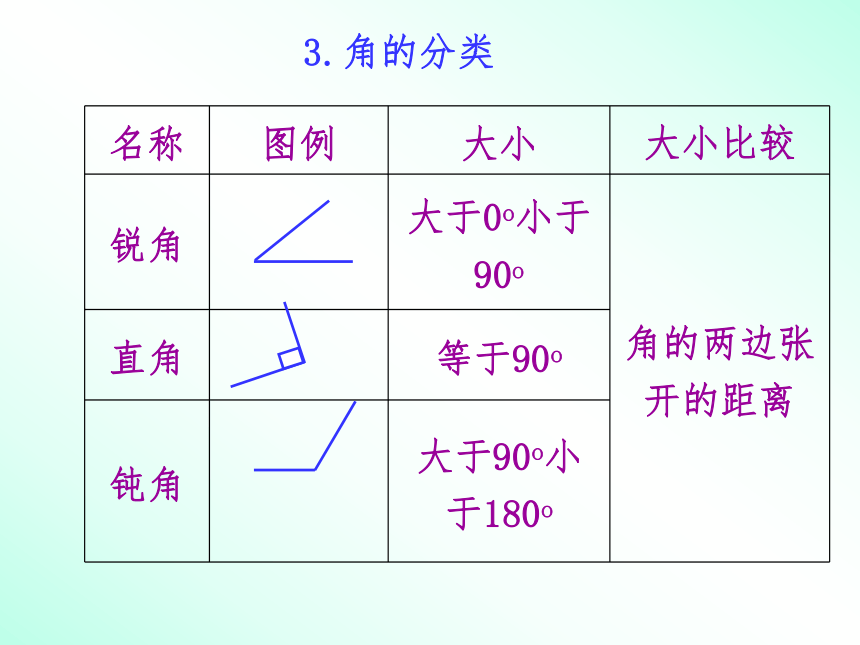
3.角的分类
名称 图例 大小 大小比较
锐角 大于0o小于90o 角的两边张开的距离
直角 等于90o
钝角 大于90o小于180o
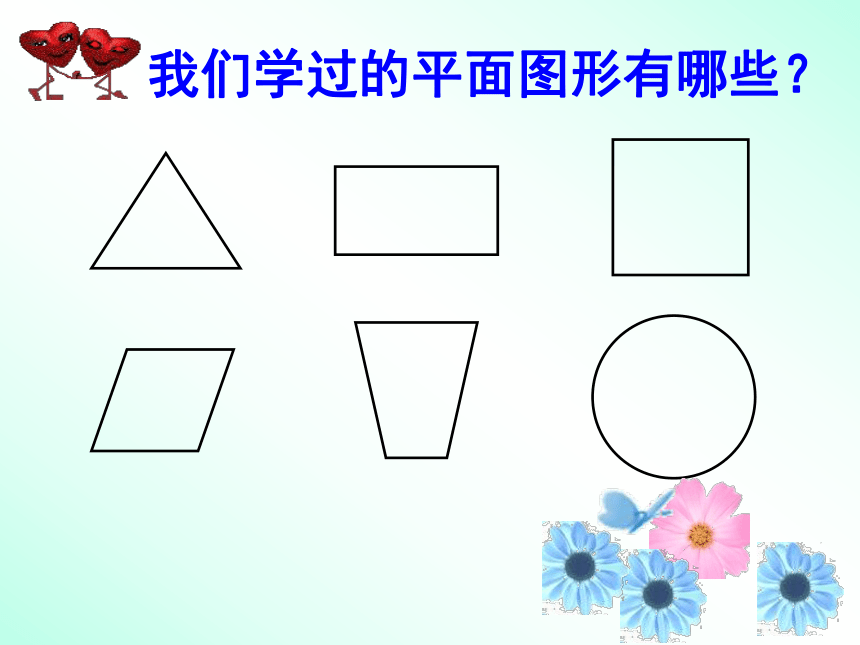
我们学过的平面图形有哪些?
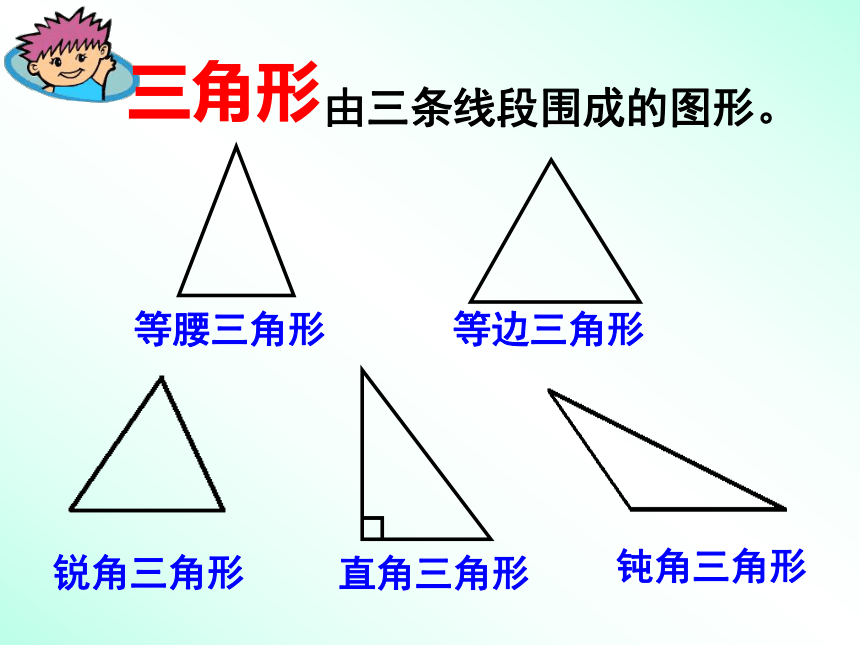
等腰三角形
等边三角形
直角三角形
钝角三角形
锐角三角形
三角形
由三条线段围成的图形。
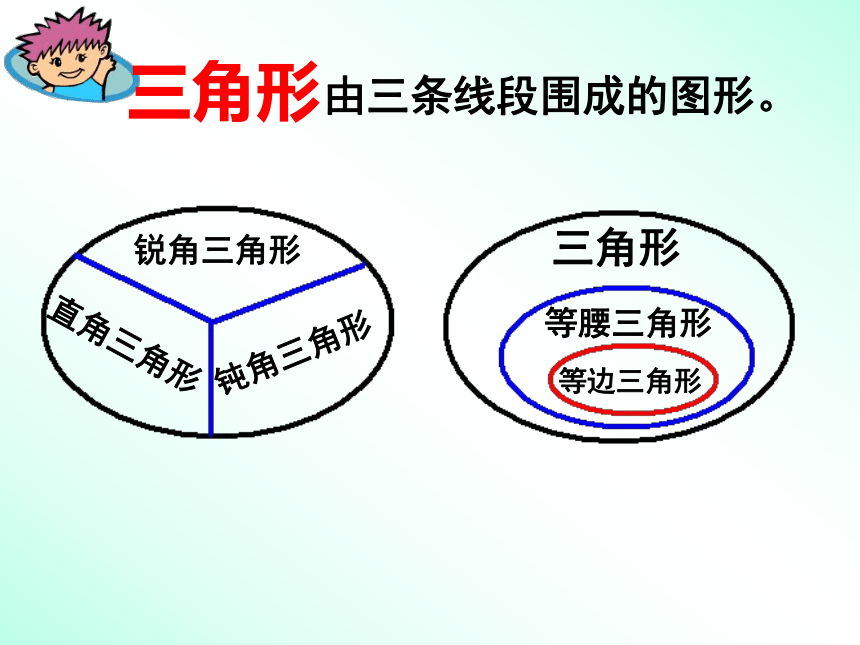
三角形
直角三角形
锐角三角形
钝角三角形
等腰三角形
三角形
等边三角形
由三条线段围成的图形。
1.三根小棒分别长3厘米、4厘米、8厘米,
它们能围成一个三角形吗?为什么?
2.一个三角形至少有几个锐角?
(2个)
3.一个三角形分成两个小三角形,每个小
三角形的内角和是多少?
(180。)
四边形
由四条线段围成的图形。
四边形
四边形
平行四边形
长方形
正方形
梯形
由四条线段围成的图形。
在下表中适当的空格内填上“√”,
再说一说几种图形之间的联系和区别。
四边形
有四个
直角
两组对
边分别
平行
只有一
组对边
平行
两组对
边分别
相等
四边
相等
正方形
长方形
平行
四边形
梯 形
√
√
√
√
√
√
√
√
√
√
圆心
O
半径
r
连接圆心和圆上任意一点的线段,叫做圆的半径。
有无数条半径,长度都相等。
同圆内,
通过圆心并且两端都在圆上的线段叫做圆的直径。
有无数条直径,长度也都相等。
d = 2r 或 r =
d
2
(曲线图形)
直径 d
A、B两镇位于河岸同侧,它们到
河岸的距离分别为AC、BD,现要在岸
边CD上建一水塔给两镇送水,问水塔
建在何处使水管最省?
最佳选择
A
B
C
D
A1
B1
F
G
E
E
建在何处使水管最省?
问水塔
画出运动的轨迹:
半径为1分米的一个圆沿边长分别为
3分米、4分米、6分米的三角形ABC滚动
一圈,求圆心经过的路程。
28
15
3.6
6
名称 端点数量 能否度量
直线 无 否
射线 一个 否
线段 两个 能
1. 直线、射线、线段的比较
2.同一平面内两条直线的位置关系的比较
位置关系 交点 图例
平行 无
相交
互相垂直 1个交点
1个垂足
3.角的分类
名称 图例 大小 大小比较
锐角 大于0o小于90o 角的两边张开的距离
直角 等于90o
钝角 大于90o小于180o
我们学过的平面图形有哪些?
等腰三角形
等边三角形
直角三角形
钝角三角形
锐角三角形
三角形
由三条线段围成的图形。
三角形
直角三角形
锐角三角形
钝角三角形
等腰三角形
三角形
等边三角形
由三条线段围成的图形。
1.三根小棒分别长3厘米、4厘米、8厘米,
它们能围成一个三角形吗?为什么?
2.一个三角形至少有几个锐角?
(2个)
3.一个三角形分成两个小三角形,每个小
三角形的内角和是多少?
(180。)
四边形
由四条线段围成的图形。
四边形
四边形
平行四边形
长方形
正方形
梯形
由四条线段围成的图形。
在下表中适当的空格内填上“√”,
再说一说几种图形之间的联系和区别。
四边形
有四个
直角
两组对
边分别
平行
只有一
组对边
平行
两组对
边分别
相等
四边
相等
正方形
长方形
平行
四边形
梯 形
√
√
√
√
√
√
√
√
√
√
圆心
O
半径
r
连接圆心和圆上任意一点的线段,叫做圆的半径。
有无数条半径,长度都相等。
同圆内,
通过圆心并且两端都在圆上的线段叫做圆的直径。
有无数条直径,长度也都相等。
d = 2r 或 r =
d
2
(曲线图形)
直径 d
A、B两镇位于河岸同侧,它们到
河岸的距离分别为AC、BD,现要在岸
边CD上建一水塔给两镇送水,问水塔
建在何处使水管最省?
最佳选择
A
B
C
D
A1
B1
F
G
E
E
建在何处使水管最省?
问水塔
画出运动的轨迹:
半径为1分米的一个圆沿边长分别为
3分米、4分米、6分米的三角形ABC滚动
一圈,求圆心经过的路程。
28
15
3.6
6
