1.3带电粒子在匀强磁场中的运动(共16张PPT)
文档属性
| 名称 | 1.3带电粒子在匀强磁场中的运动(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-28 09:52:05 | ||
图片预览





文档简介
(共16张PPT)
1.3 带电粒子在匀强磁场中的运动
复习
通电导线在磁场中所受到的安培力是大量运动电荷所受洛伦兹力的宏观表现。
1、什么是洛伦兹力?它与安培力的关系?
洛伦兹力:运动电荷在磁场中受到的力
2、洛伦兹力的方向如何判定?
洛伦兹力的方向由左手定则判定
(1)四指指正电荷的运动方向,
或指负电荷运动的反方向。
(2)洛伦兹力垂直于Β、 ν所在
的平面垂直。
3、洛伦兹力的大小如何计算?
(1)当电荷运动方向与磁场方向垂直(v⊥B)时,
F洛=qvB.
(2)当电荷运动方向与磁场方向平行(v // B)时,
电荷不受洛伦兹力.
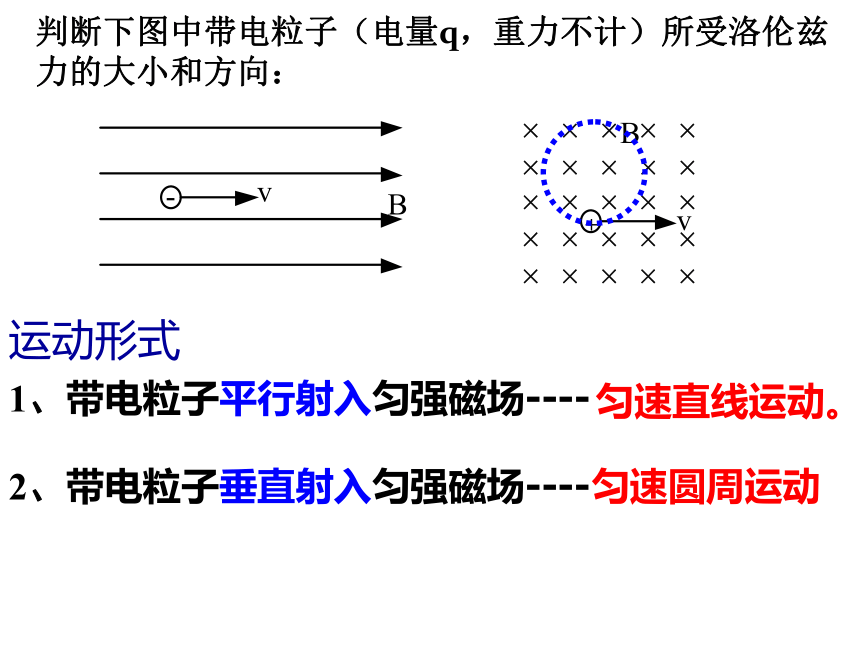
[问题]:判断下图中带电粒子(电量q,重力不计)所受洛伦兹力的大小和方向。
F洛=qvB
F洛=0
运动形式
1、带电粒子平行射入匀强磁场----匀速直线运动。
2、带电粒子垂直射入匀强磁场
V
-
F洛
V
-
F洛
V
-
F洛
V
-
F洛
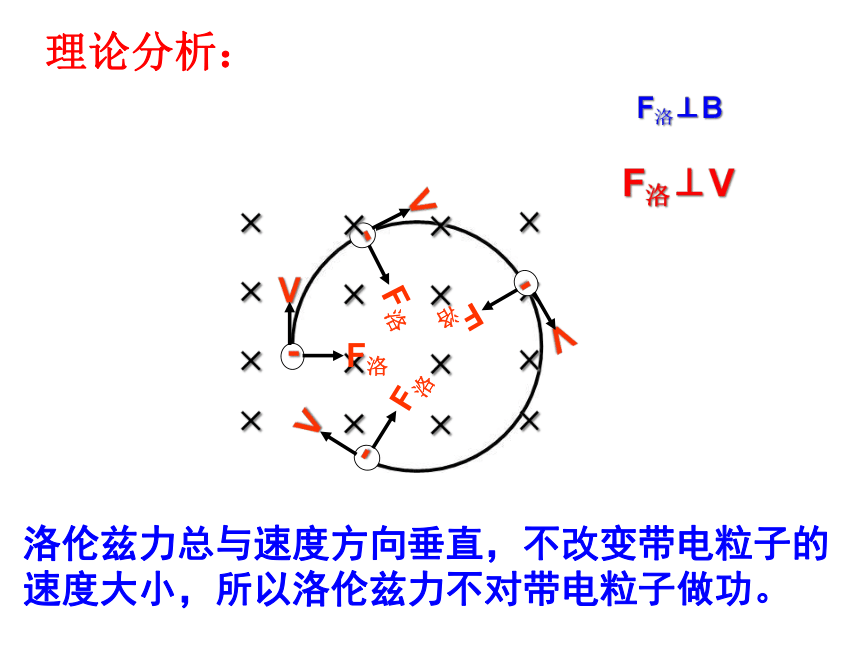
理论分析:
F洛⊥B
F洛⊥V
洛伦兹力总与速度方向垂直,不改变带电粒子的速度大小,所以洛伦兹力不对带电粒子做功。
判断下图中带电粒子(电量q,重力不计)所受洛伦兹力的大小和方向:
运动形式
1、带电粒子平行射入匀强磁场----
2、带电粒子垂直射入匀强磁场----
匀速圆周运动
匀速直线运动。
励磁线圈
玻璃泡
选择开关
一、带电粒子在匀强磁场中的运动
实验验证—洛伦兹力演示仪
电子枪
匀强磁场中带电粒子运动轨迹的半径与哪些因素有关?
可见r与速度V、磁感应强度B、粒子的比荷有关
例1:一个带电粒子,沿垂直于磁场的方向射入一匀强磁场.粒子的一段径迹如下图所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电量不变).从图中情况可以确定( )
A.粒子从a到b,带正电
B.粒子从a到b,带负电
C.粒子从b到a,带正电
D.粒子从b到a,带负电
C
匀强磁场中带电粒子运动周期与哪些因素有关?
周期T与运动速度及运动半径无关
V
V
V
V
带电粒子做圆周运动的分析方法
V
V
带电粒子做圆周运动的分析方法
(1)几个有关的角及其关系:
A
v
v
O’
α
B
θ
θ
θ‘
Φ(偏转角)
粒子速度的偏转角φ等于圆心角α,并等于AB弦与切线的夹角θ(弦切角)的2倍.即φ=α=2θ
带电粒子做圆周运动的分析方法
(2)确定圆心:
已知入射方向和出射方向, 与速度垂直的半径交点就是圆弧轨道的圆心。
已知入射方向和出射点的位置时,半径与弦中垂线的交点就是圆弧轨道的圆心。
V
P
M
O
V0
P
M
O
V
带电粒子做圆周运动的分析方法
(3)确定半径: 一般利用几何知识,常用解三角形的方法。
(4)确定运动时间:利用圆心角与弦切角的关系,或者是四边形内角和等于计算出圆心角的大小,由公式可求出运动时间。
d
B
e
θ
v
【1】如图所示,一束电子(电量为e)以速度V垂直射入磁感应强度为B、宽度为d的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为300。求 : (1) 电子的质量m= (2) 电子在磁场中的运动时间t=
d
B
e
θ
v
带电粒子在匀强磁场中的运动
平行磁感线进入:做匀速直线运动
垂直磁感线进入:做匀速圆周运动
半径:R=
mv
qB
周期:T=
2πm
qB
课堂小结
1.3 带电粒子在匀强磁场中的运动
复习
通电导线在磁场中所受到的安培力是大量运动电荷所受洛伦兹力的宏观表现。
1、什么是洛伦兹力?它与安培力的关系?
洛伦兹力:运动电荷在磁场中受到的力
2、洛伦兹力的方向如何判定?
洛伦兹力的方向由左手定则判定
(1)四指指正电荷的运动方向,
或指负电荷运动的反方向。
(2)洛伦兹力垂直于Β、 ν所在
的平面垂直。
3、洛伦兹力的大小如何计算?
(1)当电荷运动方向与磁场方向垂直(v⊥B)时,
F洛=qvB.
(2)当电荷运动方向与磁场方向平行(v // B)时,
电荷不受洛伦兹力.
[问题]:判断下图中带电粒子(电量q,重力不计)所受洛伦兹力的大小和方向。
F洛=qvB
F洛=0
运动形式
1、带电粒子平行射入匀强磁场----匀速直线运动。
2、带电粒子垂直射入匀强磁场
V
-
F洛
V
-
F洛
V
-
F洛
V
-
F洛
理论分析:
F洛⊥B
F洛⊥V
洛伦兹力总与速度方向垂直,不改变带电粒子的速度大小,所以洛伦兹力不对带电粒子做功。
判断下图中带电粒子(电量q,重力不计)所受洛伦兹力的大小和方向:
运动形式
1、带电粒子平行射入匀强磁场----
2、带电粒子垂直射入匀强磁场----
匀速圆周运动
匀速直线运动。
励磁线圈
玻璃泡
选择开关
一、带电粒子在匀强磁场中的运动
实验验证—洛伦兹力演示仪
电子枪
匀强磁场中带电粒子运动轨迹的半径与哪些因素有关?
可见r与速度V、磁感应强度B、粒子的比荷有关
例1:一个带电粒子,沿垂直于磁场的方向射入一匀强磁场.粒子的一段径迹如下图所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电量不变).从图中情况可以确定( )
A.粒子从a到b,带正电
B.粒子从a到b,带负电
C.粒子从b到a,带正电
D.粒子从b到a,带负电
C
匀强磁场中带电粒子运动周期与哪些因素有关?
周期T与运动速度及运动半径无关
V
V
V
V
带电粒子做圆周运动的分析方法
V
V
带电粒子做圆周运动的分析方法
(1)几个有关的角及其关系:
A
v
v
O’
α
B
θ
θ
θ‘
Φ(偏转角)
粒子速度的偏转角φ等于圆心角α,并等于AB弦与切线的夹角θ(弦切角)的2倍.即φ=α=2θ
带电粒子做圆周运动的分析方法
(2)确定圆心:
已知入射方向和出射方向, 与速度垂直的半径交点就是圆弧轨道的圆心。
已知入射方向和出射点的位置时,半径与弦中垂线的交点就是圆弧轨道的圆心。
V
P
M
O
V0
P
M
O
V
带电粒子做圆周运动的分析方法
(3)确定半径: 一般利用几何知识,常用解三角形的方法。
(4)确定运动时间:利用圆心角与弦切角的关系,或者是四边形内角和等于计算出圆心角的大小,由公式可求出运动时间。
d
B
e
θ
v
【1】如图所示,一束电子(电量为e)以速度V垂直射入磁感应强度为B、宽度为d的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为300。求 : (1) 电子的质量m= (2) 电子在磁场中的运动时间t=
d
B
e
θ
v
带电粒子在匀强磁场中的运动
平行磁感线进入:做匀速直线运动
垂直磁感线进入:做匀速圆周运动
半径:R=
mv
qB
周期:T=
2πm
qB
课堂小结
