沪科版数学七年级下册10.2 第4课时 平行线的判定方法2,3同步课时练习(word版含答案)
文档属性
| 名称 | 沪科版数学七年级下册10.2 第4课时 平行线的判定方法2,3同步课时练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 182.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览

文档简介
第4课时 平行线的判定方法2,3
知识点1 内错角相等,两直线平行
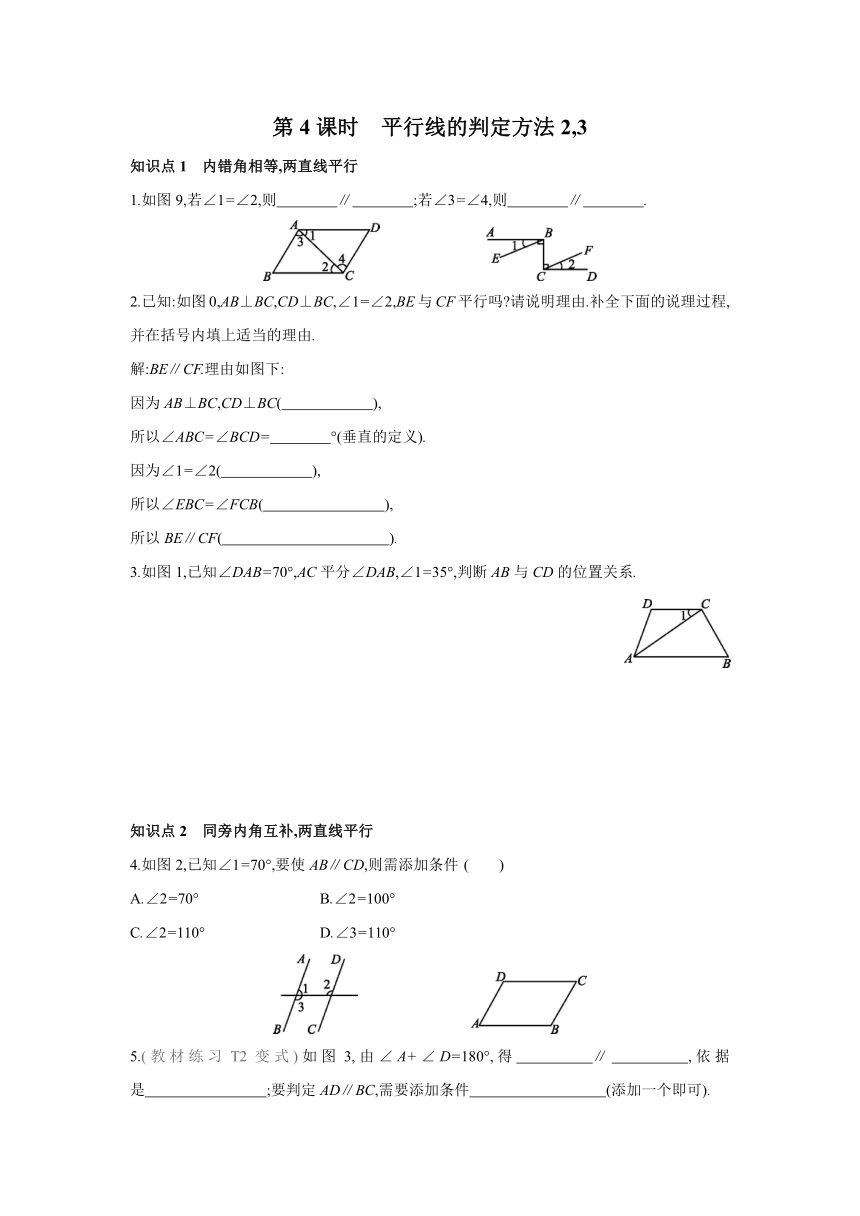
1.如图9,若∠1=∠2,则 ∥ ;若∠3=∠4,则 ∥ .
2.已知:如图0,AB⊥BC,CD⊥BC,∠1=∠2,BE与CF平行吗 请说明理由.补全下面的说理过程,并在括号内填上适当的理由.
解:BE∥CF.理由如图下:
因为AB⊥BC,CD⊥BC( ),
所以∠ABC=∠BCD= °(垂直的定义).
因为∠1=∠2( ),
所以∠EBC=∠FCB( ),
所以BE∥CF( ).
3.如图1,已知∠DAB=70°,AC平分∠DAB,∠1=35°,判断AB与CD的位置关系.
知识点2 同旁内角互补,两直线平行
4.如图2,已知∠1=70°,要使AB∥CD,则需添加条件 ( )
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
5.(教材练习T2变式)如图3,由∠A+∠D=180°,得 ∥ ,依据是 ;要判定AD∥BC,需要添加条件 (添加一个即可).
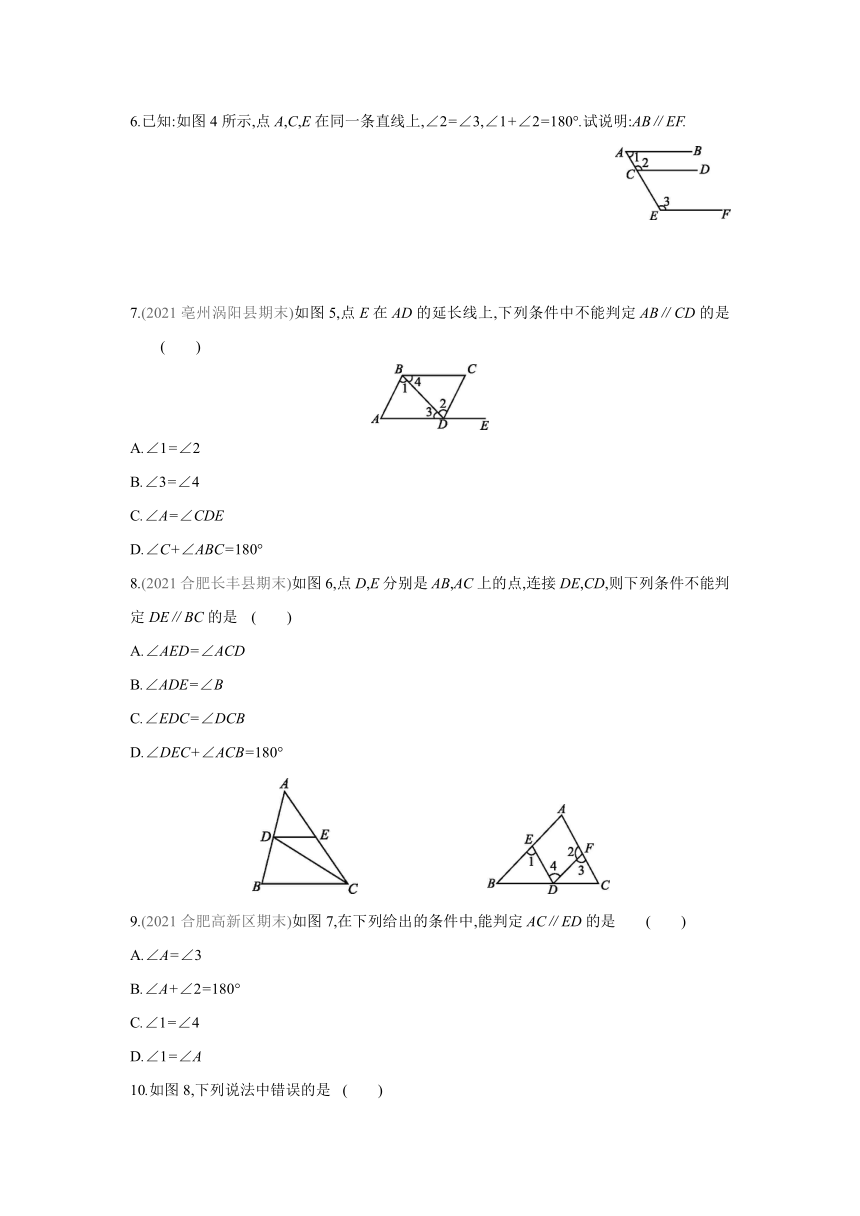
6.已知:如图4所示,点A,C,E在同一条直线上,∠2=∠3,∠1+∠2=180°.试说明:AB∥EF.
7.(2021亳州涡阳县期末)如图5,点E在AD的延长线上,下列条件中不能判定AB∥CD的是 ( )
A.∠1=∠2
B.∠3=∠4
C.∠A=∠CDE
D.∠C+∠ABC=180°
8.(2021合肥长丰县期末)如图6,点D,E分别是AB,AC上的点,连接DE,CD,则下列条件不能判定DE∥BC的是 ( )
A.∠AED=∠ACD
B.∠ADE=∠B
C.∠EDC=∠DCB
D.∠DEC+∠ACB=180°
9.(2021合肥高新区期末)如图7,在下列给出的条件中,能判定AC∥ED的是 ( )
A.∠A=∠3
B.∠A+∠2=180°
C.∠1=∠4
D.∠1=∠A
10.如图8,下列说法中错误的是 ( )
A.因为∠1=∠2,所以AE∥BD
B.因为∠5=∠1+∠3,所以AE∥BD
C.因为∠3=∠4,所以AB∥CD
D.因为∠2+∠4+∠5=180°,所以AE∥BD
11.如图9,有下列条件:①∠1=∠2;②∠3+∠4=180°;③∠5+∠6=180°;④∠2=∠3.其中能判定直线a∥b的有 ( )
A.2个 B.3个 C.4个 D.5个
12.如图0,两块三角尺的形状、大小完全相同,点B,E,F,D在同一条直线上,不添加辅助线,你能判定哪些线是平行的 依据是什么
13.如图1,∠2+∠D=180°,∠1=∠B,那么AB与EF平行吗 为什么
14.如图2,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,试判断AB与CD的位置关系,并说明理由.
答案
第4课时 平行线的判定方法2,3
1.AD BC AB CD 解决此题的关键是确定好所给两角是哪两条直线被哪条直线所截而成的内错角.发现∠1和∠2恰好是直线AD和BC被CA所截形成的内错角,所以直线AD∥BC.∠3和∠4恰好是直线AB和CD被CA所截形成的内错角,所以直线AB∥CD.
2.已知 90 已知 等角的余角相等 内错角相等,两直线平行
3.解:因为∠DAB=70°,AC平分∠DAB,
所以∠CAB=∠DAB=35°.
又因为∠1=35°,所以∠1=∠CAB,
所以AB∥CD.
4.C
5.AB CD 同旁内角互补,两直线平行 答案不唯一,如图∠A+∠B=180°
6.解:因为∠2=∠3,∠1+∠2=180°(已知),所以∠1+∠3=180°(等量代换),
所以AB∥EF(同旁内角互补,两直线平行).
7.B 因为∠1和∠2是直线AB,CD被直线BD所截得到的一对内错角,所以当∠1=∠2时,可得AB∥CD,故A选项不符合题意;
因为∠3和∠4是直线AD,BC被直线BD所截得到的一对内错角,所以当∠3=∠4时,可得AD∥BC,故B选项符合题意;
因为∠A和∠CDE是直线AB,CD被直线AE所截得到的一对同位角,所以当∠A=∠CDE时,可得AB∥CD,故C选项不符合题意;
∠C和∠ABC是直线AB,CD被直线BC所截得到的一对同旁内角,所以当∠C+∠ABC=180°时,可得AB∥CD,故D选项不符合题意.
故选B.
8.A ∠AED=∠ACD,不能判定DE∥BC,故A选项符合题意;
∠ADE=∠B,能判定DE∥BC,故B选项不符合题意;
∠EDC=∠DCB,能判定DE∥BC,故C选项不符合题意;
∠DEC+∠ACB=180°,能判定DE∥BC,故D选项不符合题意.
故选A.
9.D 因为∠A=∠3,所以AB∥DF,故A选项不符合题意;
因为∠A+∠2=180°,所以AB∥DF,故B选项不符合题意;
因为∠1=∠4,所以AB∥DF,故C选项不符合题意;
因为∠1=∠A,所以AC∥ED,故D选项符合题意.
故选D.
10.B A项,因为∠1=∠2,依据“内错角相等,两直线平行”得AE∥BD,正确,不合题意;B项,由∠5=∠1+∠3不能判定AE∥BD,错误,符合题意;C项,因为∠3=∠4,依据“内错角相等,两直线平行”得AB∥CD,正确,不合题意;D项,因为∠2+∠4+∠5=180°,依据“同旁内角互补,两直线平行”得AE∥BD,正确,不合题意.
11.B ①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b.
故能判定直线a∥b的有3个.
故选B.
12.解:能判定AB∥CD,AE∥CF.
由于两块三角尺的形状、大小完全相同,则∠ABD=∠CDB,
依据“内错角相等,两直线平行”得AB∥CD.
由于两块三角尺的形状、大小完全相同,则∠AEB=∠CFD=90°,
所以∠AED=∠CFE=90°,
依据“内错角相等,两直线平行”得AE∥CF.
13.解:AB∥EF.理由如图下:
因为∠2+∠D=180°,所以EF∥CD.
因为∠1=∠B,所以AB∥CD,所以AB∥EF.
14.解:AB∥CD.理由如图下:
因为BE平分∠ABD,DE平分∠BDC,
所以∠ABD=2∠1,∠BDC=2∠2.
因为∠1+∠2=90°,所以∠ABD+∠BDC=2(∠1+∠2)=180°,
所以AB∥CD(同旁内角互补,两直线平行).
知识点1 内错角相等,两直线平行
1.如图9,若∠1=∠2,则 ∥ ;若∠3=∠4,则 ∥ .
2.已知:如图0,AB⊥BC,CD⊥BC,∠1=∠2,BE与CF平行吗 请说明理由.补全下面的说理过程,并在括号内填上适当的理由.
解:BE∥CF.理由如图下:
因为AB⊥BC,CD⊥BC( ),
所以∠ABC=∠BCD= °(垂直的定义).
因为∠1=∠2( ),
所以∠EBC=∠FCB( ),
所以BE∥CF( ).
3.如图1,已知∠DAB=70°,AC平分∠DAB,∠1=35°,判断AB与CD的位置关系.
知识点2 同旁内角互补,两直线平行
4.如图2,已知∠1=70°,要使AB∥CD,则需添加条件 ( )
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
5.(教材练习T2变式)如图3,由∠A+∠D=180°,得 ∥ ,依据是 ;要判定AD∥BC,需要添加条件 (添加一个即可).
6.已知:如图4所示,点A,C,E在同一条直线上,∠2=∠3,∠1+∠2=180°.试说明:AB∥EF.
7.(2021亳州涡阳县期末)如图5,点E在AD的延长线上,下列条件中不能判定AB∥CD的是 ( )
A.∠1=∠2
B.∠3=∠4
C.∠A=∠CDE
D.∠C+∠ABC=180°
8.(2021合肥长丰县期末)如图6,点D,E分别是AB,AC上的点,连接DE,CD,则下列条件不能判定DE∥BC的是 ( )
A.∠AED=∠ACD
B.∠ADE=∠B
C.∠EDC=∠DCB
D.∠DEC+∠ACB=180°
9.(2021合肥高新区期末)如图7,在下列给出的条件中,能判定AC∥ED的是 ( )
A.∠A=∠3
B.∠A+∠2=180°
C.∠1=∠4
D.∠1=∠A
10.如图8,下列说法中错误的是 ( )
A.因为∠1=∠2,所以AE∥BD
B.因为∠5=∠1+∠3,所以AE∥BD
C.因为∠3=∠4,所以AB∥CD
D.因为∠2+∠4+∠5=180°,所以AE∥BD
11.如图9,有下列条件:①∠1=∠2;②∠3+∠4=180°;③∠5+∠6=180°;④∠2=∠3.其中能判定直线a∥b的有 ( )
A.2个 B.3个 C.4个 D.5个
12.如图0,两块三角尺的形状、大小完全相同,点B,E,F,D在同一条直线上,不添加辅助线,你能判定哪些线是平行的 依据是什么
13.如图1,∠2+∠D=180°,∠1=∠B,那么AB与EF平行吗 为什么
14.如图2,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,试判断AB与CD的位置关系,并说明理由.
答案
第4课时 平行线的判定方法2,3
1.AD BC AB CD 解决此题的关键是确定好所给两角是哪两条直线被哪条直线所截而成的内错角.发现∠1和∠2恰好是直线AD和BC被CA所截形成的内错角,所以直线AD∥BC.∠3和∠4恰好是直线AB和CD被CA所截形成的内错角,所以直线AB∥CD.
2.已知 90 已知 等角的余角相等 内错角相等,两直线平行
3.解:因为∠DAB=70°,AC平分∠DAB,
所以∠CAB=∠DAB=35°.
又因为∠1=35°,所以∠1=∠CAB,
所以AB∥CD.
4.C
5.AB CD 同旁内角互补,两直线平行 答案不唯一,如图∠A+∠B=180°
6.解:因为∠2=∠3,∠1+∠2=180°(已知),所以∠1+∠3=180°(等量代换),
所以AB∥EF(同旁内角互补,两直线平行).
7.B 因为∠1和∠2是直线AB,CD被直线BD所截得到的一对内错角,所以当∠1=∠2时,可得AB∥CD,故A选项不符合题意;
因为∠3和∠4是直线AD,BC被直线BD所截得到的一对内错角,所以当∠3=∠4时,可得AD∥BC,故B选项符合题意;
因为∠A和∠CDE是直线AB,CD被直线AE所截得到的一对同位角,所以当∠A=∠CDE时,可得AB∥CD,故C选项不符合题意;
∠C和∠ABC是直线AB,CD被直线BC所截得到的一对同旁内角,所以当∠C+∠ABC=180°时,可得AB∥CD,故D选项不符合题意.
故选B.
8.A ∠AED=∠ACD,不能判定DE∥BC,故A选项符合题意;
∠ADE=∠B,能判定DE∥BC,故B选项不符合题意;
∠EDC=∠DCB,能判定DE∥BC,故C选项不符合题意;
∠DEC+∠ACB=180°,能判定DE∥BC,故D选项不符合题意.
故选A.
9.D 因为∠A=∠3,所以AB∥DF,故A选项不符合题意;
因为∠A+∠2=180°,所以AB∥DF,故B选项不符合题意;
因为∠1=∠4,所以AB∥DF,故C选项不符合题意;
因为∠1=∠A,所以AC∥ED,故D选项符合题意.
故选D.
10.B A项,因为∠1=∠2,依据“内错角相等,两直线平行”得AE∥BD,正确,不合题意;B项,由∠5=∠1+∠3不能判定AE∥BD,错误,符合题意;C项,因为∠3=∠4,依据“内错角相等,两直线平行”得AB∥CD,正确,不合题意;D项,因为∠2+∠4+∠5=180°,依据“同旁内角互补,两直线平行”得AE∥BD,正确,不合题意.
11.B ①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b.
故能判定直线a∥b的有3个.
故选B.
12.解:能判定AB∥CD,AE∥CF.
由于两块三角尺的形状、大小完全相同,则∠ABD=∠CDB,
依据“内错角相等,两直线平行”得AB∥CD.
由于两块三角尺的形状、大小完全相同,则∠AEB=∠CFD=90°,
所以∠AED=∠CFE=90°,
依据“内错角相等,两直线平行”得AE∥CF.
13.解:AB∥EF.理由如图下:
因为∠2+∠D=180°,所以EF∥CD.
因为∠1=∠B,所以AB∥CD,所以AB∥EF.
14.解:AB∥CD.理由如图下:
因为BE平分∠ABD,DE平分∠BDC,
所以∠ABD=2∠1,∠BDC=2∠2.
因为∠1+∠2=90°,所以∠ABD+∠BDC=2(∠1+∠2)=180°,
所以AB∥CD(同旁内角互补,两直线平行).
