沪科版数学七年级下册10.2 第2课时 同位角、内错角、同旁内角同步课时练习(word版含答案)
文档属性
| 名称 | 沪科版数学七年级下册10.2 第2课时 同位角、内错角、同旁内角同步课时练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 263.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览

文档简介
第2课时 同位角、内错角、同旁内角
知识点1 同位角
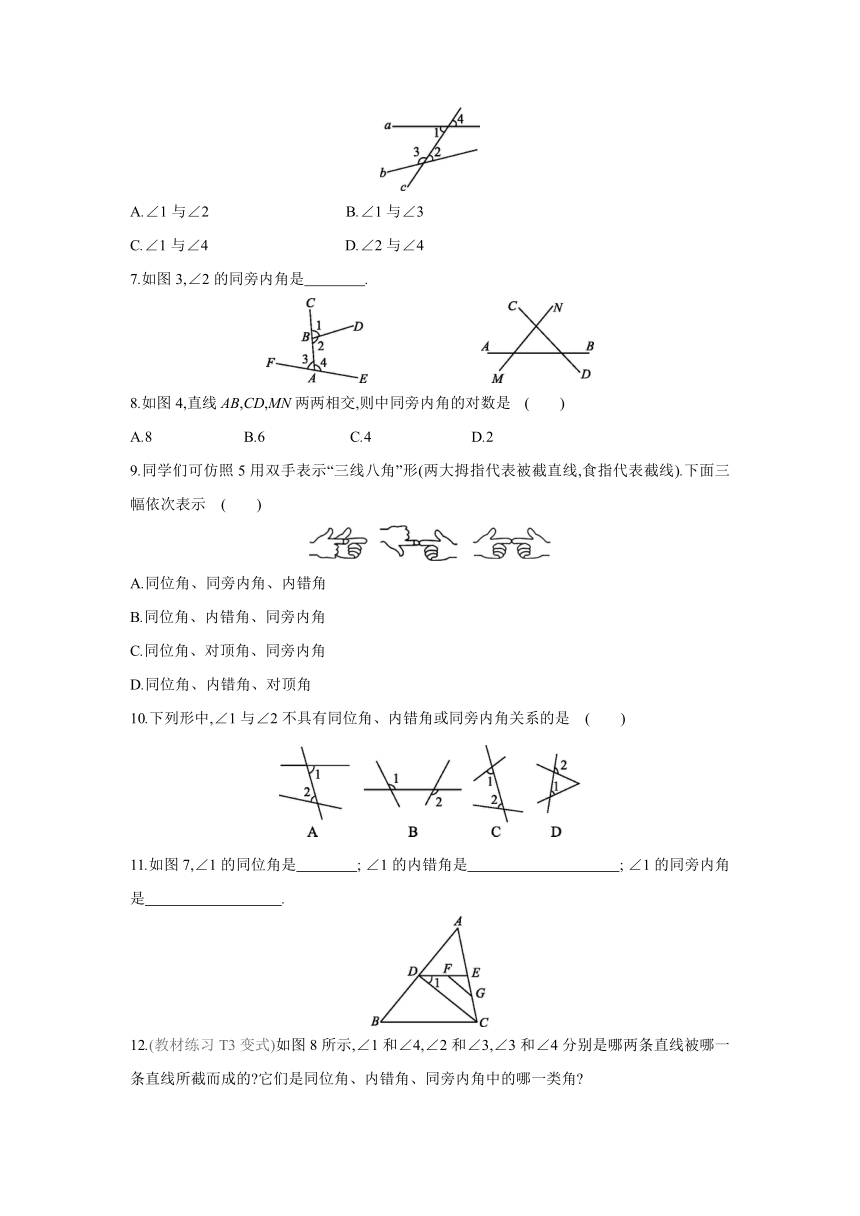
1.如图,∠1和∠2属于同位角的有 ( )
A.①②③ B.②③④ C.③④⑤ D.①②⑤
2.如图,中与∠1构成同位角的角有 个.
知识点2 内错角
3.(2021百色)如图,与∠1是内错角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
4.如图0,直线l1,l2被直线l3所截,则内错角共有 ( )
A.1对 B.2对 C.3对 D.4对
5.如图1,∠1和∠2是直线AB和AC被直线DE所截而成的 角;∠3和∠4是直线 和 被直线 所截而成的 角.
知识点3 同旁内角
6.(2021贺州)如图2,下列两个角是同旁内角的是 ( )
A.∠1与∠2 B.∠1与∠3
C.∠1与∠4 D.∠2与∠4
7.如图3,∠2的同旁内角是 .
8.如图4,直线AB,CD,MN两两相交,则中同旁内角的对数是 ( )
A.8 B.6 C.4 D.2
9.同学们可仿照5用双手表示“三线八角”形(两大拇指代表被截直线,食指代表截线).下面三幅依次表示 ( )
A.同位角、同旁内角、内错角
B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角
D.同位角、内错角、对顶角
10.下列形中,∠1与∠2不具有同位角、内错角或同旁内角关系的是 ( )
11.如图7,∠1的同位角是 ; ∠1的内错角是 ; ∠1的同旁内角是 .
12.(教材练习T3变式)如图8所示,∠1和∠4,∠2和∠3,∠3和∠4分别是哪两条直线被哪一条直线所截而成的 它们是同位角、内错角、同旁内角中的哪一类角
13.(1)如图9①,直线l1,l2被直线l3所截,在这个基本形中,形成了 对同旁内角;
(2)如图②,平面内三条直线l1,l2,l3两两相交,交点分别为A,B,C,中一共有 对同旁内角;
(3)平面内四条直线两两相交,最多可以形成 对同旁内角;
(4)平面内n(n为大于2的整数)条直线两两相交,最多可以形成 对同旁内角.
14.趣味数学:如图0,一游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如图:写出从起始角∠1跳到终点角∠3的两种不同路径,路径1:∠1∠9∠3;路径2:∠1∠12∠6∠10∠3.
试一试:从起始角∠1跳到终点角∠8.
答案
第2课时 同位角、内错角、同旁内角
1.D ①∠1和∠2是同位角,故①符合题意.
②∠1和∠2是同位角,故②符合题意.
③∠1和∠2不是同位角,故③不符合题意.
④∠1和∠2不是同位角,故④不符合题意.
⑤∠1和∠2是同位角,故⑤符合题意.
故选D.
2.3
3.C 根据内错角的定义,∠1的内错角是∠4.
故选C.
4.B
5.内错 BC DE AC 内错
∠1和∠2是直线AB和AC被直线DE所截而成的内错角;∠3和∠4是直线BC和DE被直线AC所截而成的内错角.
6.B A项,∠1与∠2是内错角,不是同旁内角,故本选项不符合题意;
B项,∠1与∠3是同旁内角,故本选项符合题意;
C项,∠1与∠4是对顶角,不是同旁内角,故本选项不符合题意;
D项,∠2与∠4是同位角,不是同旁内角,故本选项不符合题意.
故选B.
7.∠4
8.B 根据同旁内角的定义,直线AB,CD被直线MN所截可以得到两对同旁内角.
同理:直线AB,MN被直线CD所截,可以得到两对同旁内角,
直线CD,MN被直线AB所截,可以得到两对同旁内角.
因此共6对同旁内角.
9.B 根据同位角、内错角、同旁内角的概念,可知第一个是同位角,第二个是内错角,第三个是同旁内角.
10.B
11.∠EFG ∠DCB,∠AED ∠DCE,∠DFG,∠DEC
12.解:∠1和∠4是直线CE和AB被直线BD所截而成的同位角;
∠2和∠3是直线CE和AB被直线AC所截而成的内错角;
∠3和∠4是直线AC和BC被直线AB所截而成的同旁内角.
13.(1)2 (2)6 (3)24 (4)n(n-1)(n-2)
(1)直线l1,l2被直线l3所截,在这个基本形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A,B,C,中一共有3×2=6对同旁内角.
(3)平面内四条直线两两相交,交点最多为6个,最多可以形成4×(4-1)×(4-2)=24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n·(n-1)(n-2)对同旁内角.
14.解:答案不唯一,如图路径1:∠1∠12∠8;
路径2:∠1∠10∠5∠8.
知识点1 同位角
1.如图,∠1和∠2属于同位角的有 ( )
A.①②③ B.②③④ C.③④⑤ D.①②⑤
2.如图,中与∠1构成同位角的角有 个.
知识点2 内错角
3.(2021百色)如图,与∠1是内错角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
4.如图0,直线l1,l2被直线l3所截,则内错角共有 ( )
A.1对 B.2对 C.3对 D.4对
5.如图1,∠1和∠2是直线AB和AC被直线DE所截而成的 角;∠3和∠4是直线 和 被直线 所截而成的 角.
知识点3 同旁内角
6.(2021贺州)如图2,下列两个角是同旁内角的是 ( )
A.∠1与∠2 B.∠1与∠3
C.∠1与∠4 D.∠2与∠4
7.如图3,∠2的同旁内角是 .
8.如图4,直线AB,CD,MN两两相交,则中同旁内角的对数是 ( )
A.8 B.6 C.4 D.2
9.同学们可仿照5用双手表示“三线八角”形(两大拇指代表被截直线,食指代表截线).下面三幅依次表示 ( )
A.同位角、同旁内角、内错角
B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角
D.同位角、内错角、对顶角
10.下列形中,∠1与∠2不具有同位角、内错角或同旁内角关系的是 ( )
11.如图7,∠1的同位角是 ; ∠1的内错角是 ; ∠1的同旁内角是 .
12.(教材练习T3变式)如图8所示,∠1和∠4,∠2和∠3,∠3和∠4分别是哪两条直线被哪一条直线所截而成的 它们是同位角、内错角、同旁内角中的哪一类角
13.(1)如图9①,直线l1,l2被直线l3所截,在这个基本形中,形成了 对同旁内角;
(2)如图②,平面内三条直线l1,l2,l3两两相交,交点分别为A,B,C,中一共有 对同旁内角;
(3)平面内四条直线两两相交,最多可以形成 对同旁内角;
(4)平面内n(n为大于2的整数)条直线两两相交,最多可以形成 对同旁内角.
14.趣味数学:如图0,一游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如图:写出从起始角∠1跳到终点角∠3的两种不同路径,路径1:∠1∠9∠3;路径2:∠1∠12∠6∠10∠3.
试一试:从起始角∠1跳到终点角∠8.
答案
第2课时 同位角、内错角、同旁内角
1.D ①∠1和∠2是同位角,故①符合题意.
②∠1和∠2是同位角,故②符合题意.
③∠1和∠2不是同位角,故③不符合题意.
④∠1和∠2不是同位角,故④不符合题意.
⑤∠1和∠2是同位角,故⑤符合题意.
故选D.
2.3
3.C 根据内错角的定义,∠1的内错角是∠4.
故选C.
4.B
5.内错 BC DE AC 内错
∠1和∠2是直线AB和AC被直线DE所截而成的内错角;∠3和∠4是直线BC和DE被直线AC所截而成的内错角.
6.B A项,∠1与∠2是内错角,不是同旁内角,故本选项不符合题意;
B项,∠1与∠3是同旁内角,故本选项符合题意;
C项,∠1与∠4是对顶角,不是同旁内角,故本选项不符合题意;
D项,∠2与∠4是同位角,不是同旁内角,故本选项不符合题意.
故选B.
7.∠4
8.B 根据同旁内角的定义,直线AB,CD被直线MN所截可以得到两对同旁内角.
同理:直线AB,MN被直线CD所截,可以得到两对同旁内角,
直线CD,MN被直线AB所截,可以得到两对同旁内角.
因此共6对同旁内角.
9.B 根据同位角、内错角、同旁内角的概念,可知第一个是同位角,第二个是内错角,第三个是同旁内角.
10.B
11.∠EFG ∠DCB,∠AED ∠DCE,∠DFG,∠DEC
12.解:∠1和∠4是直线CE和AB被直线BD所截而成的同位角;
∠2和∠3是直线CE和AB被直线AC所截而成的内错角;
∠3和∠4是直线AC和BC被直线AB所截而成的同旁内角.
13.(1)2 (2)6 (3)24 (4)n(n-1)(n-2)
(1)直线l1,l2被直线l3所截,在这个基本形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A,B,C,中一共有3×2=6对同旁内角.
(3)平面内四条直线两两相交,交点最多为6个,最多可以形成4×(4-1)×(4-2)=24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n·(n-1)(n-2)对同旁内角.
14.解:答案不唯一,如图路径1:∠1∠12∠8;
路径2:∠1∠10∠5∠8.
