沪科新版七年级下册 第10章相交线、平行线与平移 单元测试 (word版含答案 )
文档属性
| 名称 | 沪科新版七年级下册 第10章相交线、平行线与平移 单元测试 (word版含答案 ) |
|
|
| 格式 | zip | ||
| 文件大小 | 132.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览




文档简介
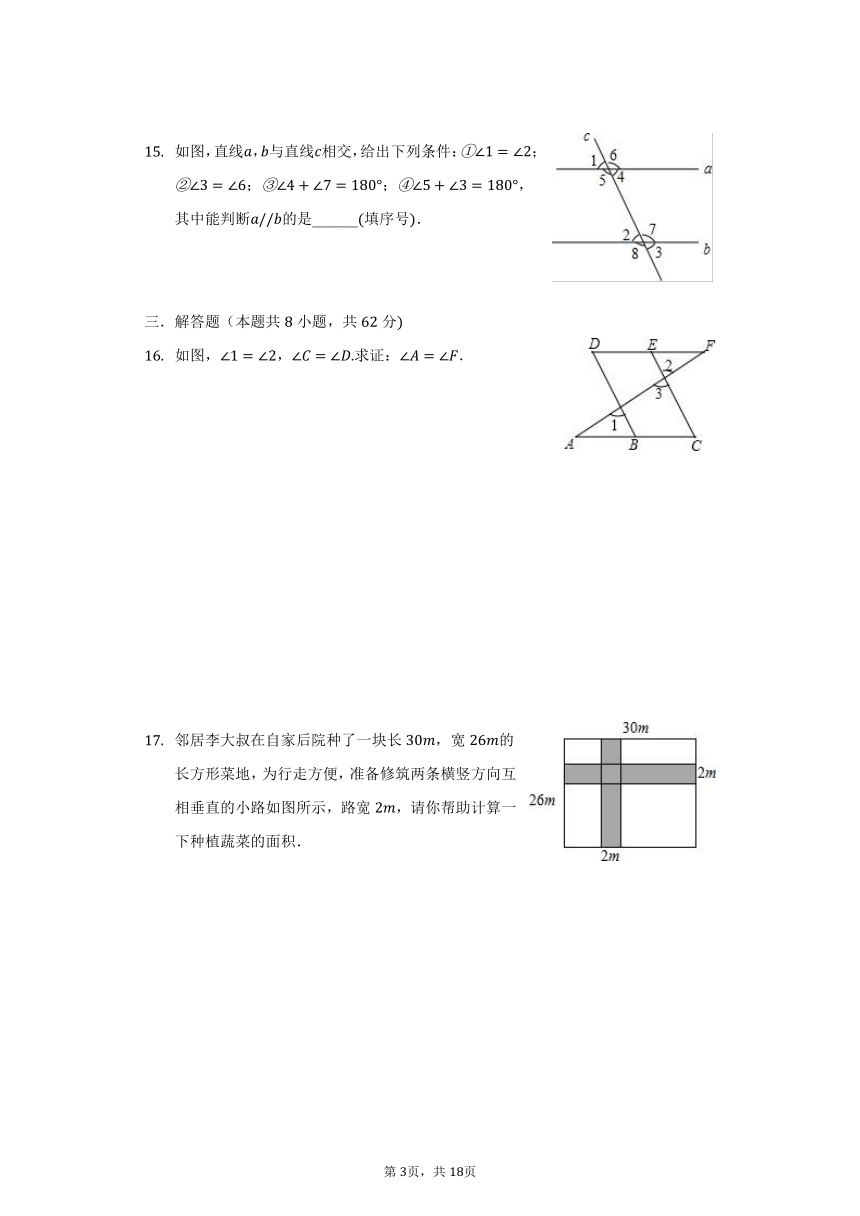
沪科新版七年级下册《第10章相交线、平行线与平移》 2022年单元测试(1)
一.选择题(本题共8小题,共24分)
在一个平面内,任意三条直线相交,交点的个数最多有
A. 个 B. 个 C. 个 D. 个
平面上不重合的两条直线,它们的位置关系只可能是
A. 相交或垂直 B. 垂直或平行 C. 相交或平行 D. 以上都不对
如图,直线,相交于点,,则
A.
B.
C.
D.
下列说法正确的是
A. 相等的角是对顶角
B. 在同一平面内,垂直于同一条直线的两条直线平行
C. 两条直线被第三条直线所截,同位角相等
D. 和为的两个角叫做邻补角
如图,已知、相交于,于,,则的度数是
A.
B.
C.
D.
如图,,,,则
A.
B.
C.
D.
下列说法:
两条直线相交,有公共顶点而没有公共边的两个角是对顶角;
如果两条线段没有交点,那么这两条线段所在直线也没有交点;
邻补角的两条角平分线构成一个直角;
直线外一点与直线上各点连接的所有线段中,垂线段最短.其中正确的是
A. 个 B. 个 C. 个 D. 个
下列说法正确的是
不相交的两条射线一定平行
B. 在同一平面内,过一点有且只有一条直线与这条直线平行
C. 在同一平面内,过一点有且只有一条直线与这条直线垂直
D. 直线外一点与直线上任一点的连线段叫做点到直线的距离
二.填空题(本题共7小题,共21分)
平面上有条直线,其中有条直线是互相平行,那么这条直线最多将平面分成______个部分.
设,,为同一平面内三条不同直线,若,,则与的位置关系是______.
如图,要得到,只需要添加一个条件,这个条件可以是______.
如图,一张长方形纸片,分别在边、上取点,,沿折叠纸片,与交于点,若,则______
如图,将一张长方形纸条沿某条直线折叠,若,则等于______.
用火柴梗搭成一条鱼如图所示,最少只要平移______根火柴梗,就能使这条鱼的方向相反.
如图,直线,与直线相交,给出下列条件:;;;,其中能判断的是______填序号.
三.解答题(本题共8小题,共62分)
如图,,求证:.
邻居李大叔在自家后院种了一块长,宽的长方形菜地,为行走方便,准备修筑两条横竖方向互相垂直的小路如图所示,路宽,请你帮助计算一下种植蔬菜的面积.
星期天早晨,小刚和爸爸正在商量往楼梯上铺地毯的事,如图所示,
爸爸:“小刚,你帮我算一下,从一层铺到二层需要地毯几米?”
小刚:“我早已用盒尺量好了,每阶高,宽为”
爸爸:打断小刚的话“不量每阶的高度和宽度,你想想有没有办法?”
小刚:思索“有了,只需要量出楼梯的总高和总长度再相加,就行了.”
你认为小刚的方法可以吗?说明理由.
如图,直线,,两两相交,,,求的度数.
如图,在边长为个单位长度的正方形网格中,三角形经过平移后得到三角形,图中标出了点的对应点根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题保留画图痕迹.
画出三角形;
连接,,那么与的数量关系是______,位置关系是______.
把向右平移格,再向上平移格,画出所得到的,并说出线段与的大小及位置关系.
如图,于,于,于,试比较四条线段、、、的大小.
如图,所有小正方形的边长都为个单位,、、均在格点上.
过点画线段的平行线;
过点画线段的垂线段,垂足为;
过点画线段的垂线,交于点;
线段______的长度是点到直线的距离;
在以上所画的图中与相等的角是______.
答案和解析
1.【答案】
【解析】
解:三条直线相交时,位置关系如图所示:
判断可知:最多有个交点,故选D.
三条直线相交,有三种情况,即:两条直线平行,被第三条直线所截,有两个交点;三条直线经过同一个点,有一个交点;三条直线两两相交且不经过同一点,有三个交点.故可得答案.
本题考查了相交线.解决本题的关键是画出三条直线相交时的三种情况,找出交点.
2.【答案】
【解析】
解:平面内的直线有平行或相交两种位置关系.
故选:.
同一平面内,直线的位置关系通常有两种:平行或相交;垂直不属于直线的位置关系,它是特殊的相交.
本题主要考查了在同一平面内的两条直线的位置关系,属于基础题,难度一般.
3.【答案】
【解析】
解:,,
,
,
故选:.
根据对顶角相等可得,再根据邻补角互补可得答案.
此题主要考查了对顶角的性质和邻补角的性质,关键是掌握对顶角相等,邻补角互补.
4.【答案】
【解析】
解:、对顶角既有大小关系,又有位置关系,相等的角是对顶角的说法错误;
B、在同一平面内,由垂直于同一条直线的两条直线,可推出同位角相等,故两直线平行,正确;
C、两条直线被第三条直线所截,只有在两直线平行的情况下,同位角相等,错误;
D、邻补角既有大小关系,又有位置关系,和为的两个角叫做邻补角说法错误.
故选:.
根据对顶角的定义,同位角相等的条件,以及邻补角的概念进行判断,逐一排除.
本题主要考查对顶角的定义,同位角相等的条件,以及邻补角的概念,一定注意结论的题设要完整.
5.【答案】
【解析】
解:,
,
,
,
,
故选:.
根据垂直的定义和对顶角相等即可求出的度数.
本题利用垂直的定义,对顶角的性质计算,要注意领会由垂直得直角这一要点.
6.【答案】
【解析】
解:如图,延长交于点;
,
,
,
,
;
故选:.
延长交于点;根据平角的定义得到,根据余角的定义得到根据平行线的性质即可得到结论.
该题主要考查了垂线的定义、平行线的性质、三角形的外角性质等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用平行线的性质、三角形的外角性质等几何知识点来分析、判断、解答.
7.【答案】
【解析】
解:两条直线相交,有公共顶点而没有公共边的两个角是对顶角,对;
直线延长可能有交点,错;
邻补角的两条角平分线构成一个直角,对;
直线外一点与直线上各点连接的所有线段中,垂线段最短,对.
故选C.
根据相关定义对各选项逐一进行判定,即可得出结论.
对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
8.【答案】
【解析】
解:、当两射线在一直线上时就不平行,故本选项错误;
B、过直线外一点有且只有一条直线平行于已知直线,故本选项错误;
C、在同一平面内,过一点有且只有一条直线垂直于已知直线,故本选项正确;
D、过直线外一点作直线的垂线,这点和垂足之间的线段的长是点到直线的距离,故本选项错误;
故选:.
根据射线在一直线上课判断;根据平行公理的推论课判断;根据点到直线的距离定义可判断;根据垂线的性质可判断.
本题考查了对平行公理及推论,垂线,点到直线的距离等知识点的应用,关键是能根据定理和性质进行判断.
9.【答案】
【解析】
解:条不平行的直线最多可将平面分成个部分,
加入第一条平行线后,它与前面的条直线共有个交点,它被分成段,每一段将原有的部分一分为二,因此增加了个部分,
同理每增加一条平行线就增加个部分,
故这条直线最多将平面分成.
故答案为.
先计算出条不平行的直线所能将平面分成的部分,然后再计算加入第一条平行线所增加的平面数量,从而可得出第二、第三、第四条加上后的总数量.
本题考查直线相交所产生平面个数的问题,有一定难度,注意先计算条不平行的直线所分成的平面数量.
10.【答案】
【解析】
解:在同一平面内,,,
,
即与的位置关系是平行,
故答案为:.
根据在同一平面内,两条直线都与同一条直线垂直,则这两直线平行作答.
本题考查了平行线的判定,解题时利用了:在同一平面内,两条直线都与同一条直线垂直,则这两直线平行.
11.【答案】
答案不唯一
【解析】
解:添加,根据“内错角相等,两直线平行”推知.
故答案是: 答案不唯一.
根据平行线的判定定理添加条件即可.
本题考查了平行线的判定方法;熟练掌握平行线的判定方法,并能进行推理论证是解决问题的关键.
12.【答案】
【解析】
解:.
,.
由折叠可得,,
.
故答案为:.
依据平行线的性质,即可得出,再根据折叠可得,,最后依据进行计算即可.
本题考查的是平行线的性质,熟记平行线的性质定理是解答此题的关键.
13.【答案】
【解析】
解:如图,,
,
由折叠可得,,
,
,
故答案为:.
依据平行线的性质以及折叠的性质,即可得到的度数.
本题考查平行线的性质,翻折变换知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
14.【答案】
【解析】
解:如图所示.
故答案为:.
分别把每竖列上的最上面的一根,移动到每竖列的最下面,改变头、尾、翅的方向即可.
本题考查平移的性质,解决本题的关键是理解只需改变尾,翅和头的方向就能改变方向.
15.【答案】
【解析】
解:,
,故此选项正确;
无法得出,故此选项错误;
,
,故此选项正确;
,
,
,故此选项正确;
故答案为:.
直接利用平行线的判定方法分别分析得出答案.
此题主要考查了平行线的判定,正确把握平行线的几种判定方法是解题关键.
16.【答案】
证明:,,
.
.
.
又,
.
.
.
【解析】
首先证明,根据平行线的性质可得到,然后根据,证明,即可得到,根据平行线的性质即可证得.
本题考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
17.【答案】
解:由平移,可把种植蔬菜的面积看成是如图边长为米和米的矩形的面积.
所以种植蔬菜的面积为:米
【解析】
根据平移的知识,把横竖各两条道路平移到正方形的边上,求剩余空白部分的面积即可.
此题主要考查了生活中的平移现象,利用平移的知识,把图形变换位置,可以简化计算,在实际生活中,应用很广.
18.【答案】
解:可以,
如图所示:根据图示可得:地毯的总长度.
【解析】
根据平移可得地毯的总长度.
此题主要考查了生活中的平移现象,关键是把楼梯每一节的长和宽移到一起.
19.【答案】
解:根据对顶角相等,得,
,
,
.
【解析】
结合,利用对顶角相等的性质求出的度数,再求的度数.
本题考查对顶角的性质,是一个需要熟记的内容.
20.【答案】
【解析】
解:如图,即为所求;
,.
故答案为:,.
利用平移变换的性质分别作出,的对应点,即可;
利用平移变换的性质判断即可.
本题考查作图平移变换,全等三角形的判定和性质等知识,解题的关键是掌握平移变换的性质,属于中考常考题型.
21.【答案】
解:如图,为所作,线段与平行且相等.
【解析】
本题考查了作图平移变换:确定平移后图形的基本要素平移方向、平移距离作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
利用网格特点和平移的性质画出点、、的对应点、、即可得到,然后根据平移的性质判断线段与的大小及位置关系.
22.【答案】
解:,
,
,
,
,
,
.
【解析】
分别根据垂线段最短依次进行判断,然后按照从小到大的顺序排列即可.
本题考查了垂线段最短的性质,是基础题,熟记性质并准确识图是解题的关键.
23.【答案】
直线为所作,
线段为所作;
直线为所作;
;
【解析】
解:
见答案;
见答案;
见答案;
线段的长度是点到直线的距离;
故答案为:.
,
,,
,
即在以上所画的图中与相等的角是,
故答案为:.
【分析】
根据平行线的定义作图可得;
根据垂线的定义作图可得;
根据垂线的定义作图可得;
根据点到直线的距离可得答案;
由同角的余角相等,并结合作图及所标字母可得.
本题主要考查作图应用与设计作图,解题的关键是掌握直线和垂线及点到直线的距离的概念、同角的余角相等的性质.
第2页,共2页
第1页,共1页
一.选择题(本题共8小题,共24分)
在一个平面内,任意三条直线相交,交点的个数最多有
A. 个 B. 个 C. 个 D. 个
平面上不重合的两条直线,它们的位置关系只可能是
A. 相交或垂直 B. 垂直或平行 C. 相交或平行 D. 以上都不对
如图,直线,相交于点,,则
A.
B.
C.
D.
下列说法正确的是
A. 相等的角是对顶角
B. 在同一平面内,垂直于同一条直线的两条直线平行
C. 两条直线被第三条直线所截,同位角相等
D. 和为的两个角叫做邻补角
如图,已知、相交于,于,,则的度数是
A.
B.
C.
D.
如图,,,,则
A.
B.
C.
D.
下列说法:
两条直线相交,有公共顶点而没有公共边的两个角是对顶角;
如果两条线段没有交点,那么这两条线段所在直线也没有交点;
邻补角的两条角平分线构成一个直角;
直线外一点与直线上各点连接的所有线段中,垂线段最短.其中正确的是
A. 个 B. 个 C. 个 D. 个
下列说法正确的是
不相交的两条射线一定平行
B. 在同一平面内,过一点有且只有一条直线与这条直线平行
C. 在同一平面内,过一点有且只有一条直线与这条直线垂直
D. 直线外一点与直线上任一点的连线段叫做点到直线的距离
二.填空题(本题共7小题,共21分)
平面上有条直线,其中有条直线是互相平行,那么这条直线最多将平面分成______个部分.
设,,为同一平面内三条不同直线,若,,则与的位置关系是______.
如图,要得到,只需要添加一个条件,这个条件可以是______.
如图,一张长方形纸片,分别在边、上取点,,沿折叠纸片,与交于点,若,则______
如图,将一张长方形纸条沿某条直线折叠,若,则等于______.
用火柴梗搭成一条鱼如图所示,最少只要平移______根火柴梗,就能使这条鱼的方向相反.
如图,直线,与直线相交,给出下列条件:;;;,其中能判断的是______填序号.
三.解答题(本题共8小题,共62分)
如图,,求证:.
邻居李大叔在自家后院种了一块长,宽的长方形菜地,为行走方便,准备修筑两条横竖方向互相垂直的小路如图所示,路宽,请你帮助计算一下种植蔬菜的面积.
星期天早晨,小刚和爸爸正在商量往楼梯上铺地毯的事,如图所示,
爸爸:“小刚,你帮我算一下,从一层铺到二层需要地毯几米?”
小刚:“我早已用盒尺量好了,每阶高,宽为”
爸爸:打断小刚的话“不量每阶的高度和宽度,你想想有没有办法?”
小刚:思索“有了,只需要量出楼梯的总高和总长度再相加,就行了.”
你认为小刚的方法可以吗?说明理由.
如图,直线,,两两相交,,,求的度数.
如图,在边长为个单位长度的正方形网格中,三角形经过平移后得到三角形,图中标出了点的对应点根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题保留画图痕迹.
画出三角形;
连接,,那么与的数量关系是______,位置关系是______.
把向右平移格,再向上平移格,画出所得到的,并说出线段与的大小及位置关系.
如图,于,于,于,试比较四条线段、、、的大小.
如图,所有小正方形的边长都为个单位,、、均在格点上.
过点画线段的平行线;
过点画线段的垂线段,垂足为;
过点画线段的垂线,交于点;
线段______的长度是点到直线的距离;
在以上所画的图中与相等的角是______.
答案和解析
1.【答案】
【解析】
解:三条直线相交时,位置关系如图所示:
判断可知:最多有个交点,故选D.
三条直线相交,有三种情况,即:两条直线平行,被第三条直线所截,有两个交点;三条直线经过同一个点,有一个交点;三条直线两两相交且不经过同一点,有三个交点.故可得答案.
本题考查了相交线.解决本题的关键是画出三条直线相交时的三种情况,找出交点.
2.【答案】
【解析】
解:平面内的直线有平行或相交两种位置关系.
故选:.
同一平面内,直线的位置关系通常有两种:平行或相交;垂直不属于直线的位置关系,它是特殊的相交.
本题主要考查了在同一平面内的两条直线的位置关系,属于基础题,难度一般.
3.【答案】
【解析】
解:,,
,
,
故选:.
根据对顶角相等可得,再根据邻补角互补可得答案.
此题主要考查了对顶角的性质和邻补角的性质,关键是掌握对顶角相等,邻补角互补.
4.【答案】
【解析】
解:、对顶角既有大小关系,又有位置关系,相等的角是对顶角的说法错误;
B、在同一平面内,由垂直于同一条直线的两条直线,可推出同位角相等,故两直线平行,正确;
C、两条直线被第三条直线所截,只有在两直线平行的情况下,同位角相等,错误;
D、邻补角既有大小关系,又有位置关系,和为的两个角叫做邻补角说法错误.
故选:.
根据对顶角的定义,同位角相等的条件,以及邻补角的概念进行判断,逐一排除.
本题主要考查对顶角的定义,同位角相等的条件,以及邻补角的概念,一定注意结论的题设要完整.
5.【答案】
【解析】
解:,
,
,
,
,
故选:.
根据垂直的定义和对顶角相等即可求出的度数.
本题利用垂直的定义,对顶角的性质计算,要注意领会由垂直得直角这一要点.
6.【答案】
【解析】
解:如图,延长交于点;
,
,
,
,
;
故选:.
延长交于点;根据平角的定义得到,根据余角的定义得到根据平行线的性质即可得到结论.
该题主要考查了垂线的定义、平行线的性质、三角形的外角性质等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用平行线的性质、三角形的外角性质等几何知识点来分析、判断、解答.
7.【答案】
【解析】
解:两条直线相交,有公共顶点而没有公共边的两个角是对顶角,对;
直线延长可能有交点,错;
邻补角的两条角平分线构成一个直角,对;
直线外一点与直线上各点连接的所有线段中,垂线段最短,对.
故选C.
根据相关定义对各选项逐一进行判定,即可得出结论.
对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
8.【答案】
【解析】
解:、当两射线在一直线上时就不平行,故本选项错误;
B、过直线外一点有且只有一条直线平行于已知直线,故本选项错误;
C、在同一平面内,过一点有且只有一条直线垂直于已知直线,故本选项正确;
D、过直线外一点作直线的垂线,这点和垂足之间的线段的长是点到直线的距离,故本选项错误;
故选:.
根据射线在一直线上课判断;根据平行公理的推论课判断;根据点到直线的距离定义可判断;根据垂线的性质可判断.
本题考查了对平行公理及推论,垂线,点到直线的距离等知识点的应用,关键是能根据定理和性质进行判断.
9.【答案】
【解析】
解:条不平行的直线最多可将平面分成个部分,
加入第一条平行线后,它与前面的条直线共有个交点,它被分成段,每一段将原有的部分一分为二,因此增加了个部分,
同理每增加一条平行线就增加个部分,
故这条直线最多将平面分成.
故答案为.
先计算出条不平行的直线所能将平面分成的部分,然后再计算加入第一条平行线所增加的平面数量,从而可得出第二、第三、第四条加上后的总数量.
本题考查直线相交所产生平面个数的问题,有一定难度,注意先计算条不平行的直线所分成的平面数量.
10.【答案】
【解析】
解:在同一平面内,,,
,
即与的位置关系是平行,
故答案为:.
根据在同一平面内,两条直线都与同一条直线垂直,则这两直线平行作答.
本题考查了平行线的判定,解题时利用了:在同一平面内,两条直线都与同一条直线垂直,则这两直线平行.
11.【答案】
答案不唯一
【解析】
解:添加,根据“内错角相等,两直线平行”推知.
故答案是: 答案不唯一.
根据平行线的判定定理添加条件即可.
本题考查了平行线的判定方法;熟练掌握平行线的判定方法,并能进行推理论证是解决问题的关键.
12.【答案】
【解析】
解:.
,.
由折叠可得,,
.
故答案为:.
依据平行线的性质,即可得出,再根据折叠可得,,最后依据进行计算即可.
本题考查的是平行线的性质,熟记平行线的性质定理是解答此题的关键.
13.【答案】
【解析】
解:如图,,
,
由折叠可得,,
,
,
故答案为:.
依据平行线的性质以及折叠的性质,即可得到的度数.
本题考查平行线的性质,翻折变换知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
14.【答案】
【解析】
解:如图所示.
故答案为:.
分别把每竖列上的最上面的一根,移动到每竖列的最下面,改变头、尾、翅的方向即可.
本题考查平移的性质,解决本题的关键是理解只需改变尾,翅和头的方向就能改变方向.
15.【答案】
【解析】
解:,
,故此选项正确;
无法得出,故此选项错误;
,
,故此选项正确;
,
,
,故此选项正确;
故答案为:.
直接利用平行线的判定方法分别分析得出答案.
此题主要考查了平行线的判定,正确把握平行线的几种判定方法是解题关键.
16.【答案】
证明:,,
.
.
.
又,
.
.
.
【解析】
首先证明,根据平行线的性质可得到,然后根据,证明,即可得到,根据平行线的性质即可证得.
本题考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
17.【答案】
解:由平移,可把种植蔬菜的面积看成是如图边长为米和米的矩形的面积.
所以种植蔬菜的面积为:米
【解析】
根据平移的知识,把横竖各两条道路平移到正方形的边上,求剩余空白部分的面积即可.
此题主要考查了生活中的平移现象,利用平移的知识,把图形变换位置,可以简化计算,在实际生活中,应用很广.
18.【答案】
解:可以,
如图所示:根据图示可得:地毯的总长度.
【解析】
根据平移可得地毯的总长度.
此题主要考查了生活中的平移现象,关键是把楼梯每一节的长和宽移到一起.
19.【答案】
解:根据对顶角相等,得,
,
,
.
【解析】
结合,利用对顶角相等的性质求出的度数,再求的度数.
本题考查对顶角的性质,是一个需要熟记的内容.
20.【答案】
【解析】
解:如图,即为所求;
,.
故答案为:,.
利用平移变换的性质分别作出,的对应点,即可;
利用平移变换的性质判断即可.
本题考查作图平移变换,全等三角形的判定和性质等知识,解题的关键是掌握平移变换的性质,属于中考常考题型.
21.【答案】
解:如图,为所作,线段与平行且相等.
【解析】
本题考查了作图平移变换:确定平移后图形的基本要素平移方向、平移距离作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
利用网格特点和平移的性质画出点、、的对应点、、即可得到,然后根据平移的性质判断线段与的大小及位置关系.
22.【答案】
解:,
,
,
,
,
,
.
【解析】
分别根据垂线段最短依次进行判断,然后按照从小到大的顺序排列即可.
本题考查了垂线段最短的性质,是基础题,熟记性质并准确识图是解题的关键.
23.【答案】
直线为所作,
线段为所作;
直线为所作;
;
【解析】
解:
见答案;
见答案;
见答案;
线段的长度是点到直线的距离;
故答案为:.
,
,,
,
即在以上所画的图中与相等的角是,
故答案为:.
【分析】
根据平行线的定义作图可得;
根据垂线的定义作图可得;
根据垂线的定义作图可得;
根据点到直线的距离可得答案;
由同角的余角相等,并结合作图及所标字母可得.
本题主要考查作图应用与设计作图,解题的关键是掌握直线和垂线及点到直线的距离的概念、同角的余角相等的性质.
第2页,共2页
第1页,共1页
