人教版数学八年级下册18.2.2.1菱形 课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.2.1菱形 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
18.2.2 菱形
第一课时
学习目标:
1.理解菱形的概念,会用菱形的性质解决简单的问题;
2.经历类比矩形探究菱形性质的过程,通过观察、类比、猜想、证明等活动,体会几何图形研究的一般步骤和方法.
学习重点:
菱形性质的探索、证明和应用.
学习难点:
菱形性质的探究.
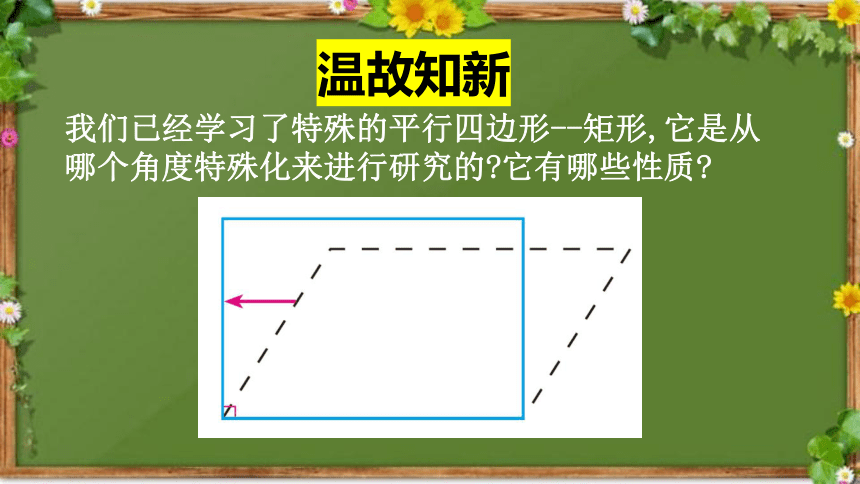
我们已经学习了特殊的平行四边形--矩形,它是从哪个角度特殊化来进行研究的 它有哪些性质
温故知新
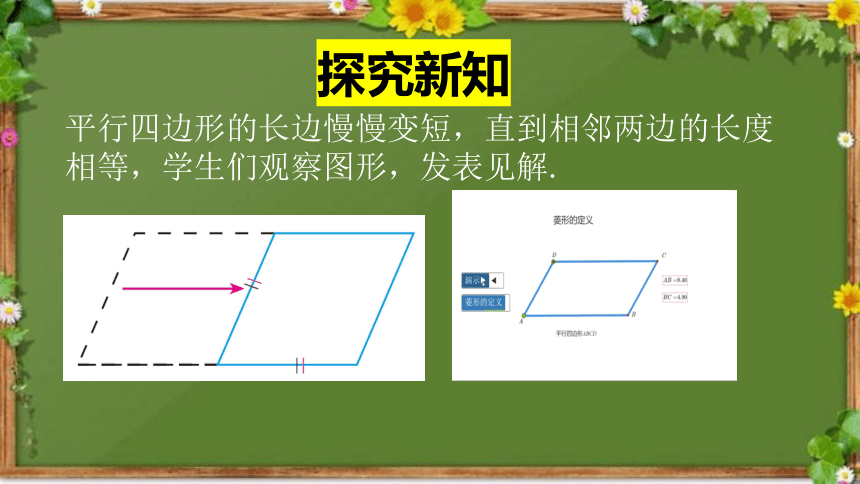
平行四边形的长边慢慢变短,直到相邻两边的长度相等,学生们观察图形,发表见解.
探究新知
菱形的定义
一组邻边相等的平行四边形叫做菱形.
生活中的菱形
学生思考:你还能举出生活中菱形的实际例子吗?
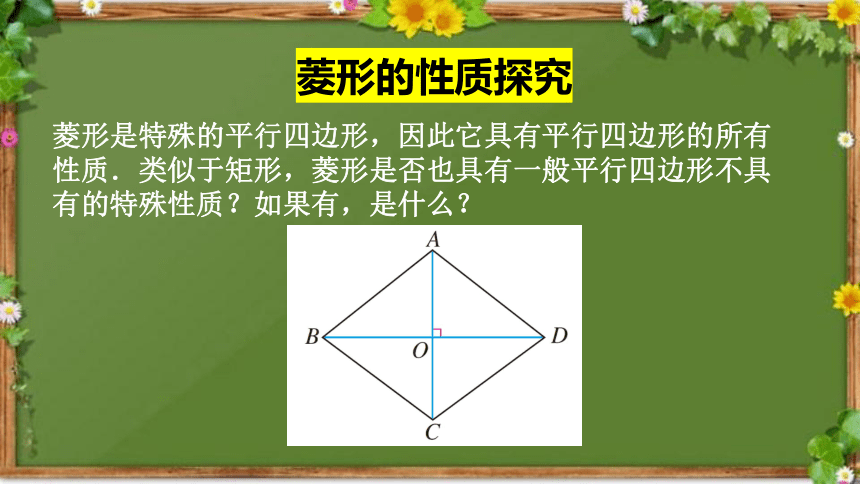
菱形的性质探究
菱形是特殊的平行四边形,因此它具有平行四边形的所有性质.类似于矩形,菱形是否也具有一般平行四边形不具有的特殊性质?如果有,是什么?
动手操作
1.将一张矩形的纸对折再对折,沿对折的部分剪下一直角三角形,打开,你发现这是一个什么样的图形
2.菱形是不是轴对称图形 如果是,它有几条对称轴
3.菱形除了具有平行四边形的性质以外,它还有什么特殊性质呢 它的边、对角线之间有什么关系
4.你能证明上述结论吗
视频演示
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证: (1)AB = BC = CD =AD;
(2)AC⊥BD;
∠1=∠2,∠3=∠4,
∠5=∠6,∠7=∠8.
菱形的性质证明
菱形的性质定理
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
边:菱形的四条边相等;
对角线:对角线互相垂直,且每一条对角线平分一组对角.
几何语言:
∵四边形ABCD是菱形
∴AB=BC=CD=DA
AC⊥BD,
∠1=∠2,∠3=∠4
∠5=∠6,∠7=∠8
探究菱形的面积公式思考:
(1)怎样求菱形的面积
(2)你发现菱形被对角线分成的四个小三角形有什么特点 菱形是否还有其他的求面积的方法
菱形的面积公式
菱形的面积公式:
(1)一般平行四边形面积公式:
面积=底×高
即:S菱形ABCD=AE×BC
(2)菱形面积还等于四个小直角三角形面积和.可推导出:
S菱形ABCD= AC×BD
菱形的面积公式
如图:四边形ABCD是菱形,对角线AC、BD交于点O,AE⊥BC于点E,若AC=a,BD=b.
E
例1:如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长.
菱形的性质应用
例2:如图,菱形花坛ABCD 的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.
(1)求两条小路的长(结果保留小数点后两位)
(2)求花坛的面积(结果保留小数点后一位)
菱形的性质应用
A
B
C
D
O
课堂练习:如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
求:四边形OBEC的面积.
菱形的性质应用
(1)什么样的图形叫做菱形?菱形与平行四边形有什么关系?
(2)菱形具有哪些性质?哪些是一般平行四边形所具有的?哪些是一般平行四边形不具有的?菱形的性质与矩形的性质有什么相同点和不同点?
(3)结合本节课的学习,谈谈你的收获.
课堂小结
教科书第57页练习1,2;
教科书第60页习题18.2第5,7题.
作业布置
18.2.2 菱形
第一课时
学习目标:
1.理解菱形的概念,会用菱形的性质解决简单的问题;
2.经历类比矩形探究菱形性质的过程,通过观察、类比、猜想、证明等活动,体会几何图形研究的一般步骤和方法.
学习重点:
菱形性质的探索、证明和应用.
学习难点:
菱形性质的探究.
我们已经学习了特殊的平行四边形--矩形,它是从哪个角度特殊化来进行研究的 它有哪些性质
温故知新
平行四边形的长边慢慢变短,直到相邻两边的长度相等,学生们观察图形,发表见解.
探究新知
菱形的定义
一组邻边相等的平行四边形叫做菱形.
生活中的菱形
学生思考:你还能举出生活中菱形的实际例子吗?
菱形的性质探究
菱形是特殊的平行四边形,因此它具有平行四边形的所有性质.类似于矩形,菱形是否也具有一般平行四边形不具有的特殊性质?如果有,是什么?
动手操作
1.将一张矩形的纸对折再对折,沿对折的部分剪下一直角三角形,打开,你发现这是一个什么样的图形
2.菱形是不是轴对称图形 如果是,它有几条对称轴
3.菱形除了具有平行四边形的性质以外,它还有什么特殊性质呢 它的边、对角线之间有什么关系
4.你能证明上述结论吗
视频演示
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证: (1)AB = BC = CD =AD;
(2)AC⊥BD;
∠1=∠2,∠3=∠4,
∠5=∠6,∠7=∠8.
菱形的性质证明
菱形的性质定理
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
边:菱形的四条边相等;
对角线:对角线互相垂直,且每一条对角线平分一组对角.
几何语言:
∵四边形ABCD是菱形
∴AB=BC=CD=DA
AC⊥BD,
∠1=∠2,∠3=∠4
∠5=∠6,∠7=∠8
探究菱形的面积公式思考:
(1)怎样求菱形的面积
(2)你发现菱形被对角线分成的四个小三角形有什么特点 菱形是否还有其他的求面积的方法
菱形的面积公式
菱形的面积公式:
(1)一般平行四边形面积公式:
面积=底×高
即:S菱形ABCD=AE×BC
(2)菱形面积还等于四个小直角三角形面积和.可推导出:
S菱形ABCD= AC×BD
菱形的面积公式
如图:四边形ABCD是菱形,对角线AC、BD交于点O,AE⊥BC于点E,若AC=a,BD=b.
E
例1:如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长.
菱形的性质应用
例2:如图,菱形花坛ABCD 的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.
(1)求两条小路的长(结果保留小数点后两位)
(2)求花坛的面积(结果保留小数点后一位)
菱形的性质应用
A
B
C
D
O
课堂练习:如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
求:四边形OBEC的面积.
菱形的性质应用
(1)什么样的图形叫做菱形?菱形与平行四边形有什么关系?
(2)菱形具有哪些性质?哪些是一般平行四边形所具有的?哪些是一般平行四边形不具有的?菱形的性质与矩形的性质有什么相同点和不同点?
(3)结合本节课的学习,谈谈你的收获.
课堂小结
教科书第57页练习1,2;
教科书第60页习题18.2第5,7题.
作业布置
