人教新版九年级下册第29章 投影与视图单元测试卷(word版含解析)
文档属性
| 名称 | 人教新版九年级下册第29章 投影与视图单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 352.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 14:32:28 | ||
图片预览

文档简介
人教新版九年级下册《第29章投影与视图》 2022年单元测试卷(1)
副标题
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,共30.0分)
下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是
A. B. C. D.
发展工业是强国之梦的重要举措,如图所示零件的左视图是
A. B. C. D.
如图,某剧院舞台上的照明灯射出的光线成“锥体”,其“锥体”面图的“锥角”是已知舞台是边长为的正方形.要使灯光能照射到整个舞台,则灯的悬挂高度是
A.
B.
C.
D.
如图,太阳光线与地面成的角,照在地面的一只排球上,排球在地面的投影长是,则排球的直径是
A.
B.
C.
D.
一个空心的圆柱如图所示,那么它的主视图是
A.
B.
C.
D.
如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是
A. 越来越小
B. 越来越大
C. 大小不变
D. 不能确定
在下面的四个几何体中,它们各自的主视图与左视图可能相同的是
A. B. C. D.
如图是某几何体的三视图,下列判断正确的是
A. 几何体是圆柱体,高为
B. 几何体是圆锥体,高为
C. 几何体是圆柱体,半径为
D. 几何体是圆锥体,直径为
下列四个几何体的俯视图中与众不同的是
A. B. C. D.
如图所示,当小人向建筑物靠近时,在建筑物上形成的盲区
A. 变大
B. 变小
C. 不变
D. 无法确定
二、填空题(本大题共9小题,共27.0分)
墙壁上处有一盏灯如图,小明站在处测得他的影长与身长相等,都为,他向墙壁走到处时发现影子刚好落在点,则灯泡与地面的距离______.
如图,电影胶片上每一个图片的规格为,放映屏幕的规格为,若放映机的光源距胶片,那么光源距屏幕______米时,放映的图象刚好布满整个屏幕.
圆柱的主视图是长方形,左视图是______形,俯视图是______形.
从正面和左面看到长方体的图形如图所示单位:,则从其上面看到图形的面积是______ .
如图,小丽站在米高的楼顶远眺前方的广场,米处有一个高为米的障碍物,那么离楼房______的范围内小丽看不见.
长方体的主视图、俯视图如图,则其左视图面积为______.
如图是由若干个棱长为的小正方体组合而成的一个几何体的三视图,则这个几何体的表面积是______ .
直角坐标系内,身高为米的小强面向轴站在轴上的点处,他的前方米处有一堵墙,已知墙高米,则站立的小强观察轴时,盲区视力达不到的地方范围是______.
如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上不改变原几何体中小立方块的位置,继续添加相同的小立方块,以搭成一个大长方体,至少还需要______个小立方块.
三、解答题(本大题共7小题,共56.0分)
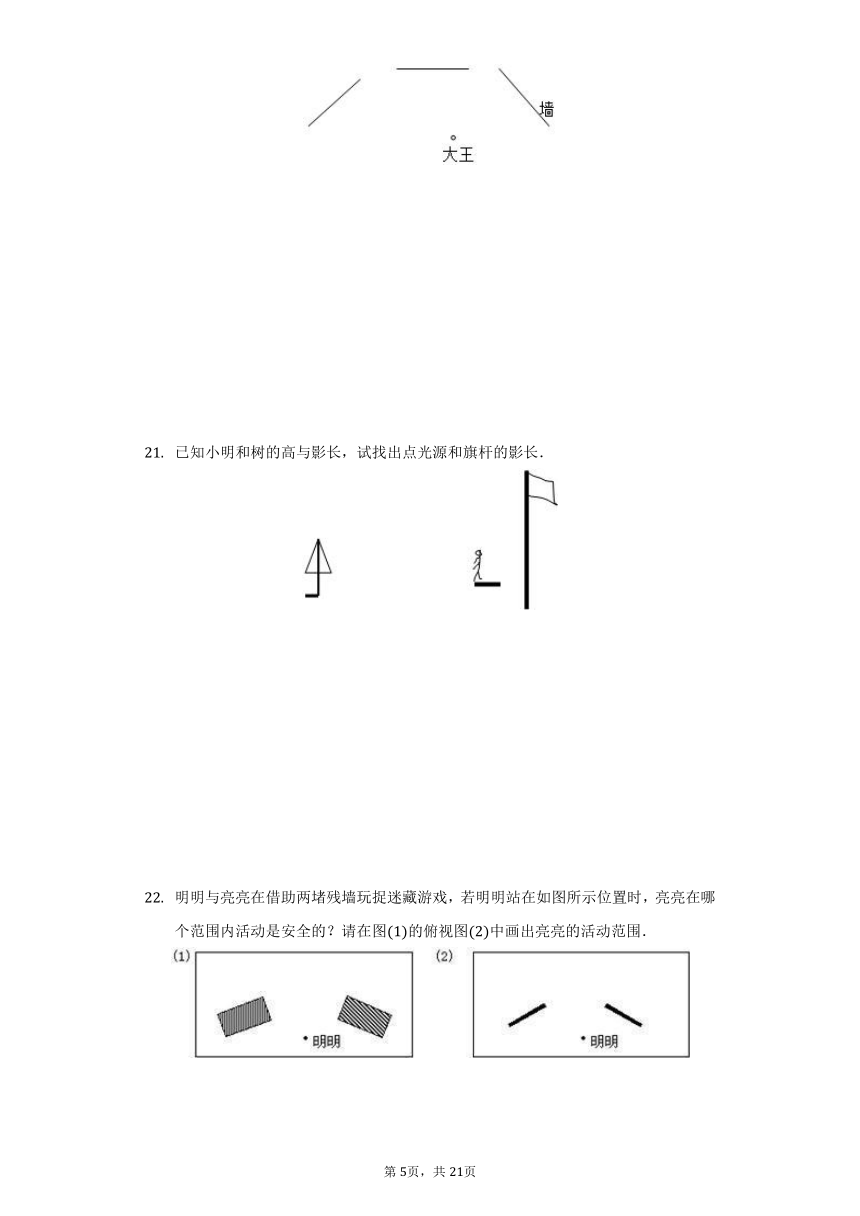
作图题:如图所示:大王站在墙前,小明站在墙后,小明不能让大王看见,请你画出小明的活动区域.
已知小明和树的高与影长,试找出点光源和旗杆的影长.
明明与亮亮在借助两堵残墙玩捉迷藏游戏,若明明站在如图所示位置时,亮亮在哪个范围内活动是安全的?请在图的俯视图中画出亮亮的活动范围.
我们坐公共汽车下车后,不要从车前车后猛跑,为什么?
一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为,的矩形,求圆柱的表面积和体积.
一个圆柱体形零件,削去了占底面圆的四分之一部分的柱体如图,现已画出了主视图与俯视图.
请只用直尺和圆规,将此零件的左视图画在规定的位置不必写作法,只须保留作图痕迹;
若此零件底面圆的半径,高,求此零件的表面积.
如图所示,一幢楼房背后有一台阶,台阶每层高米,且米,米.设太阳光线与水平地面的夹角为,当时,测得楼房在地面上的影长米,现有一只小猫睡在台阶的这层上晒太阳.
求楼房的高度约为多少米?
过了一会儿,当时,问小猫能否还晒到太阳?请说明理由.参考数据:,,
答案和解析
1.【答案】
【解析】
解:西为,西北为,东北为,东为,
将它们按时间先后顺序排列为.
故选:.
根据从早晨到傍晚物体影子的指向是:西西北北东北东,影长由长变短,再变长.
本题考查了平行投影的特点和规律.在不同时刻,物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚物体影子的指向是:西西北北东北东,影长由长变短,再变长.
2.【答案】
【解析】
【分析】
本题考查了简单组合体的三视图,从左边看得到的图形是左视图,注意看到的线画实线.根据从左边看得到的图形是左视图,可得答案.
【解答】
解:从左边看是一个矩形平均分成个,
故选:.
3.【答案】
【解析】
解:连接,
,
,
是边长为的正方形,
,
,
,
故选:.
先根据题意进行连接,再根据“锥体”面图的“锥角”是得出是等边三角形,再根据它的计算方法和正方形的特点分别进行计算,即可求出答案.
本题主要考查了中心投影和圆锥的计算,解题的关键是根据等边三角形和正方形的计算方法进行计算.
4.【答案】
【解析】
解:如图,点与点为太阳光线与球的切点,
则为排球的直径,,,
在中,,
所以,
即排球的直径为.
故选:.
由于太阳光线为平行光线,根据切线的性质得到为排球的直径,,,在中,利用正弦的定义可计算出的长,从而得到排球的直径.
本题考查了解直角三角形和平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影;平行投影中物体与投影面平行时的投影是全等的.
5.【答案】
【解析】
解:根据主视图的定义,得出它的主视图是:
故选:.
根据主视图的定义,从前面看,得出图形是一个矩形它里面含一个小矩形,即得出了答案.
本题考查了对简单组合的三视图的应用,通过做此题培养了学生的理解能力和观察能力,同时也培养了学生的空间想象能力.
6.【答案】
【解析】
解:灯光下,涉及中心投影,根据中心投影的特点灯光下影子与物体离灯源距离有关,此距离越大,影子才越小.
故选:.
解答本题关键是要区分开平行投影和中心投影.根据题意,灯光下影子越长的物体就越高,可联系到中心投影的特点,从而得出答案.
此题主要考查了中心投影的特点和规律.中心投影的特点是:等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长;
等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
7.【答案】
【解析】
解:、此几何体主视图与左视图不相同,故此选项错误;
B、立方体的主视图与左视图都是矩形,故此选项正确;
B、三棱柱主视图是矩形,左视图也是矩形,矩形宽不相同,故此选项错误;
D、四棱柱的主视图是矩形,左视图也是矩形,矩形宽不相同,故此选项错误;
故选:.
分别找到从上面看和正面看所得到的图形即可.
此题主要考查了简单几何体的三视图,关键是掌握所看的位置.
8.【答案】
【解析】
解:根据主视图和左视图为矩形是柱体,根据俯视图是圆可判断出这个几何体应该是圆柱,
再根据左视图的高度得出圆柱体的高为;
故选:.
根据主视图和左视图为矩形,得出该几何体是柱体,再根据俯视图是圆可判断出这个几何体应该是圆柱,然后根据俯视图的高即可得出答案.
本题考查由三视图确定几何体的形状,如果有两个视图为三角形,该几何体一定是锥体,如果有两个矩形,该几何体一定是柱体,其底面由第三个视图的形状决定.
9.【答案】
【解析】
解:、的俯视图是第一列两个小正方形,第二列一个小正方形,
B、的俯视图是第一列是两个小正方形,第二列是两个小正方形,
C、的俯视图是第一列两个小正方形,第二列一个小正方形,
D、的俯视图是第一列两个小正方形,第二列一个小正方形,
故选:.
根据从上边看得到的图形是俯视图,可得答案.
本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.
10.【答案】
【解析】
解:如图所示:当小人向建筑物靠近时,在建筑物上形成的盲区不断增大,
故选:.
根据盲区即看不到的建筑物的高度.根据各物体的比例关系画出图形,数形结合,可以比较直观列出相关的比例关系式,从而得出答案.
此题主要考查了学生对中心投影的理解以及利用数形结合的思想解题的能力,并结合考查了解方程组,综合性较强,难度较大,是各种考试考查的重点.其中数形结合的思想是数学中一种重要的解题思想,学生平时要加强这方面的训练.
11.【答案】
【解析】
解:如图:
根据题意得:,
∽,∽
::,::
设,,则,,则
即,
解得:,
把代入,
解得:,
故答案为:
利用相似三角形的相似比,列出方程组,通过解方程组求出灯泡与地面的距离即可.
考查了中心投影,本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程组,通过解方程组求出灯泡与地面的距离.
12.【答案】
【解析】
解:运用位似图形的性质可得设银幕距镜头,
,
所以.
,
答:银幕应在离镜头,放映的图象刚好布满整个银幕.
此题考查了位似的知识及相似三角形的性质,即位似图形都相似.
此题考查了位似图形的性质,还考查了相似三角形的性质,相似三角形的对应高的比等于相似比.解题的关键是将实际问题转化为数学问题进行解答.
13.【答案】
长方 圆
【解析】
解:圆柱的主视图是长方形,左视图是长方形,俯视图是圆形.
从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.
本题考查了几何体的三视图的判断.
14.【答案】
【解析】
解:根据从左面、从正面看到的形状图的相关数据可得:
从上面看到的形状图是长为宽为的长方形,
则从上面看到的形状图的面积是;
故答案为:.
先根据从左面、从正面看到的形状图的相关数据可得,从上面看到的形状图是长为宽为的长方形,再根据长方形的面积公式计算即可.
此题考查了由三视图判断几何体,关键是根据从左面、从正面看到的形状图的相关数据得出从上面看到的形状图是长为宽为的长方形.
15.【答案】
大于米小于米
【解析】
解:由题意得,盲区为,
设,则,
,
解得:,
在大于米小于米的范围内小丽看不见.
故答案为:大于米小于米.
先判断出盲区,然后利用解直角三角形的知识求出盲区即可.
本题考查盲区及解直角三角形的知识,难度不大,关键是找出盲区.
16.【答案】
【解析】
解:由主视图可得长方体的高为,长为,
由俯视图可得宽为,
则左视图的面积为;
故答案为:.
根据主视图可得到长方体的长和高,俯视图可得到长方体的宽,左视图表现长方体的宽和高,让宽高即为左视图的面积.
此题考查了由三视图判断几何体,根据其他视图得到几何体的长和高是解决本题的关键.
17.【答案】
【解析】
【分析】
本题考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”是解题的关键.利用主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而判断图形形状,即可得出小正方体的个数.
【解答】
解:综合三视图,我们可以得出,这个几何模型的底层有个小正方体,第二层有个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是个.
这个几何体的表面积是,
故答案为.
18.【答案】
【解析】
解:过作于,交于,,,
三角形中,::,
因此三角形中,
因此,因此盲区的范围在.
如图,本题所求的就是的值,过作于,交于,利用三角函数可求出.
利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
19.【答案】
【解析】
解:由主视图可知,搭成的几何体有三层,且有列;由左视图可知,搭成的几何体共有行;
第一层有个正方体,第二层有个正方体,第三层有个正方体,
共有个正方体,
搭在这个几何体的基础上添加相同大小的小正方体,以搭成一个大长方体,
搭成的大长方体的共有个小正方体,
至少还需要个小正方体.
故答案为:.
先由主视图、左视图、俯视图求出原来的几何体共有个正方体,再根据搭成的大长方体的共有个小正方体,即可得出答案.
本题考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查,关键是求出搭成的大长方体共有多少个小正方体.
20.【答案】
解:如图,小明的活动区域是、、三个阴影部分区域.
【解析】
根据题意用阴影部分表示出小明的活动区域,,即可.
本题考查作图应用与设计作图,解题的关键是理解题意,灵活运用所学知识解决问题.
21.【答案】
解:如图:连接、并延长交与点,点即为点光源,为旗杆的影子.
【解析】
首先根据小明的身高和影长与树的高度和影长确定点光源,然后由过点光源和旗杆的顶部确定旗杆的影长即可.
本题考查了中心投影的知识,中心投影是由点光源发出的,确定了点光源是解决本题的关键.
22.【答案】
解:阴影部分、为亮亮活动的范围.
【解析】
亮亮活动的安全范围其实就是明明的盲区,因此画亮亮的活动范围只要画出明明的盲区就行了.
本题是结合实际问题来考查学生对视点,视角和盲区的理解能力.
23.【答案】
解:因为汽车司机的视线在车前车后有看不见的地方,即盲区.
汽车前进或倒退时,在车前或车后走很容易出危险.
【解析】
根据汽车司机的视线在车前车后有看不见的地方,很容易出危险,得出坐公共汽车下车后,不要从车前车后猛跑.
此题主要考查了视点、视角和盲区,根据汽车司机的视线在车前车后有盲区进而得出答案是解题关键.
24.【答案】
解:一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为,的矩形,
当圆柱底面圆的半径为,高为,
则圆柱的表面积为:,
体积为:;
当圆柱底面圆的半径为,高为
则圆柱的表面积为:,
体积为:
【解析】
根据平行投影的性质得出当圆柱底面圆的半径为,高为,当圆柱底面圆的半径为,高为,进而分别求出其表面积和体积即可.
此题主要考查了平行投影以及圆柱体的体积公式与表面积公式,得出圆柱体的底面圆的半径结合分类讨论求出答案是解题关键.
25.【答案】
左视图与主视图形状相同,有作垂线直角的痕迹作法不唯一.
两个底面积:;
侧面积:;
表面积:
【解析】
由削去了占底面圆的四分之一部分的柱体易得主视图和左视图相同,可先画一条线段等于主视图中大长方形的长,然后分别做两个端点的垂线及线段的垂直平分线,在两端点的垂线上分别截取主视图的高连接即可得到几何体的左视图;
此零件的表面积两个底面积侧面积,把相关数值代入即可求解.
解决本题的关键是得到零件全面积的等量关系,注意侧面积的展开图应为一个长方形,长方形的长为四分之三圆的周长半径长.
26.【答案】
解:当时,在中,
,
,
即楼房的高度约为米;
当时,小猫不能再晒到太阳,
理由如下:假设没有台阶,当时,从点射下的光线与地面交于点,此时的影长,
设的延长线交于点,
,,
,
设直线与交于点,则,
,
点在上,
大楼的影子落在这个侧面上,
小猫不能晒到太阳.
【解析】
在中,由,即可求出,进而得出答案;
假设没有台阶,当时,从点射下的光线与地面的交点为点,与的交点为点,由,可得,进而判断即可.
本题考查了解直角三角形的应用,锐角三角函数定义,理解题意,将实际问题转化为数学问题是解题的关键.
第2页,共2页
第1页,共1页
副标题
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,共30.0分)
下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是
A. B. C. D.
发展工业是强国之梦的重要举措,如图所示零件的左视图是
A. B. C. D.
如图,某剧院舞台上的照明灯射出的光线成“锥体”,其“锥体”面图的“锥角”是已知舞台是边长为的正方形.要使灯光能照射到整个舞台,则灯的悬挂高度是
A.
B.
C.
D.
如图,太阳光线与地面成的角,照在地面的一只排球上,排球在地面的投影长是,则排球的直径是
A.
B.
C.
D.
一个空心的圆柱如图所示,那么它的主视图是
A.
B.
C.
D.
如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是
A. 越来越小
B. 越来越大
C. 大小不变
D. 不能确定
在下面的四个几何体中,它们各自的主视图与左视图可能相同的是
A. B. C. D.
如图是某几何体的三视图,下列判断正确的是
A. 几何体是圆柱体,高为
B. 几何体是圆锥体,高为
C. 几何体是圆柱体,半径为
D. 几何体是圆锥体,直径为
下列四个几何体的俯视图中与众不同的是
A. B. C. D.
如图所示,当小人向建筑物靠近时,在建筑物上形成的盲区
A. 变大
B. 变小
C. 不变
D. 无法确定
二、填空题(本大题共9小题,共27.0分)
墙壁上处有一盏灯如图,小明站在处测得他的影长与身长相等,都为,他向墙壁走到处时发现影子刚好落在点,则灯泡与地面的距离______.
如图,电影胶片上每一个图片的规格为,放映屏幕的规格为,若放映机的光源距胶片,那么光源距屏幕______米时,放映的图象刚好布满整个屏幕.
圆柱的主视图是长方形,左视图是______形,俯视图是______形.
从正面和左面看到长方体的图形如图所示单位:,则从其上面看到图形的面积是______ .
如图,小丽站在米高的楼顶远眺前方的广场,米处有一个高为米的障碍物,那么离楼房______的范围内小丽看不见.
长方体的主视图、俯视图如图,则其左视图面积为______.
如图是由若干个棱长为的小正方体组合而成的一个几何体的三视图,则这个几何体的表面积是______ .
直角坐标系内,身高为米的小强面向轴站在轴上的点处,他的前方米处有一堵墙,已知墙高米,则站立的小强观察轴时,盲区视力达不到的地方范围是______.
如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上不改变原几何体中小立方块的位置,继续添加相同的小立方块,以搭成一个大长方体,至少还需要______个小立方块.
三、解答题(本大题共7小题,共56.0分)
作图题:如图所示:大王站在墙前,小明站在墙后,小明不能让大王看见,请你画出小明的活动区域.
已知小明和树的高与影长,试找出点光源和旗杆的影长.
明明与亮亮在借助两堵残墙玩捉迷藏游戏,若明明站在如图所示位置时,亮亮在哪个范围内活动是安全的?请在图的俯视图中画出亮亮的活动范围.
我们坐公共汽车下车后,不要从车前车后猛跑,为什么?
一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为,的矩形,求圆柱的表面积和体积.
一个圆柱体形零件,削去了占底面圆的四分之一部分的柱体如图,现已画出了主视图与俯视图.
请只用直尺和圆规,将此零件的左视图画在规定的位置不必写作法,只须保留作图痕迹;
若此零件底面圆的半径,高,求此零件的表面积.
如图所示,一幢楼房背后有一台阶,台阶每层高米,且米,米.设太阳光线与水平地面的夹角为,当时,测得楼房在地面上的影长米,现有一只小猫睡在台阶的这层上晒太阳.
求楼房的高度约为多少米?
过了一会儿,当时,问小猫能否还晒到太阳?请说明理由.参考数据:,,
答案和解析
1.【答案】
【解析】
解:西为,西北为,东北为,东为,
将它们按时间先后顺序排列为.
故选:.
根据从早晨到傍晚物体影子的指向是:西西北北东北东,影长由长变短,再变长.
本题考查了平行投影的特点和规律.在不同时刻,物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚物体影子的指向是:西西北北东北东,影长由长变短,再变长.
2.【答案】
【解析】
【分析】
本题考查了简单组合体的三视图,从左边看得到的图形是左视图,注意看到的线画实线.根据从左边看得到的图形是左视图,可得答案.
【解答】
解:从左边看是一个矩形平均分成个,
故选:.
3.【答案】
【解析】
解:连接,
,
,
是边长为的正方形,
,
,
,
故选:.
先根据题意进行连接,再根据“锥体”面图的“锥角”是得出是等边三角形,再根据它的计算方法和正方形的特点分别进行计算,即可求出答案.
本题主要考查了中心投影和圆锥的计算,解题的关键是根据等边三角形和正方形的计算方法进行计算.
4.【答案】
【解析】
解:如图,点与点为太阳光线与球的切点,
则为排球的直径,,,
在中,,
所以,
即排球的直径为.
故选:.
由于太阳光线为平行光线,根据切线的性质得到为排球的直径,,,在中,利用正弦的定义可计算出的长,从而得到排球的直径.
本题考查了解直角三角形和平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影;平行投影中物体与投影面平行时的投影是全等的.
5.【答案】
【解析】
解:根据主视图的定义,得出它的主视图是:
故选:.
根据主视图的定义,从前面看,得出图形是一个矩形它里面含一个小矩形,即得出了答案.
本题考查了对简单组合的三视图的应用,通过做此题培养了学生的理解能力和观察能力,同时也培养了学生的空间想象能力.
6.【答案】
【解析】
解:灯光下,涉及中心投影,根据中心投影的特点灯光下影子与物体离灯源距离有关,此距离越大,影子才越小.
故选:.
解答本题关键是要区分开平行投影和中心投影.根据题意,灯光下影子越长的物体就越高,可联系到中心投影的特点,从而得出答案.
此题主要考查了中心投影的特点和规律.中心投影的特点是:等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长;
等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
7.【答案】
【解析】
解:、此几何体主视图与左视图不相同,故此选项错误;
B、立方体的主视图与左视图都是矩形,故此选项正确;
B、三棱柱主视图是矩形,左视图也是矩形,矩形宽不相同,故此选项错误;
D、四棱柱的主视图是矩形,左视图也是矩形,矩形宽不相同,故此选项错误;
故选:.
分别找到从上面看和正面看所得到的图形即可.
此题主要考查了简单几何体的三视图,关键是掌握所看的位置.
8.【答案】
【解析】
解:根据主视图和左视图为矩形是柱体,根据俯视图是圆可判断出这个几何体应该是圆柱,
再根据左视图的高度得出圆柱体的高为;
故选:.
根据主视图和左视图为矩形,得出该几何体是柱体,再根据俯视图是圆可判断出这个几何体应该是圆柱,然后根据俯视图的高即可得出答案.
本题考查由三视图确定几何体的形状,如果有两个视图为三角形,该几何体一定是锥体,如果有两个矩形,该几何体一定是柱体,其底面由第三个视图的形状决定.
9.【答案】
【解析】
解:、的俯视图是第一列两个小正方形,第二列一个小正方形,
B、的俯视图是第一列是两个小正方形,第二列是两个小正方形,
C、的俯视图是第一列两个小正方形,第二列一个小正方形,
D、的俯视图是第一列两个小正方形,第二列一个小正方形,
故选:.
根据从上边看得到的图形是俯视图,可得答案.
本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.
10.【答案】
【解析】
解:如图所示:当小人向建筑物靠近时,在建筑物上形成的盲区不断增大,
故选:.
根据盲区即看不到的建筑物的高度.根据各物体的比例关系画出图形,数形结合,可以比较直观列出相关的比例关系式,从而得出答案.
此题主要考查了学生对中心投影的理解以及利用数形结合的思想解题的能力,并结合考查了解方程组,综合性较强,难度较大,是各种考试考查的重点.其中数形结合的思想是数学中一种重要的解题思想,学生平时要加强这方面的训练.
11.【答案】
【解析】
解:如图:
根据题意得:,
∽,∽
::,::
设,,则,,则
即,
解得:,
把代入,
解得:,
故答案为:
利用相似三角形的相似比,列出方程组,通过解方程组求出灯泡与地面的距离即可.
考查了中心投影,本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程组,通过解方程组求出灯泡与地面的距离.
12.【答案】
【解析】
解:运用位似图形的性质可得设银幕距镜头,
,
所以.
,
答:银幕应在离镜头,放映的图象刚好布满整个银幕.
此题考查了位似的知识及相似三角形的性质,即位似图形都相似.
此题考查了位似图形的性质,还考查了相似三角形的性质,相似三角形的对应高的比等于相似比.解题的关键是将实际问题转化为数学问题进行解答.
13.【答案】
长方 圆
【解析】
解:圆柱的主视图是长方形,左视图是长方形,俯视图是圆形.
从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.
本题考查了几何体的三视图的判断.
14.【答案】
【解析】
解:根据从左面、从正面看到的形状图的相关数据可得:
从上面看到的形状图是长为宽为的长方形,
则从上面看到的形状图的面积是;
故答案为:.
先根据从左面、从正面看到的形状图的相关数据可得,从上面看到的形状图是长为宽为的长方形,再根据长方形的面积公式计算即可.
此题考查了由三视图判断几何体,关键是根据从左面、从正面看到的形状图的相关数据得出从上面看到的形状图是长为宽为的长方形.
15.【答案】
大于米小于米
【解析】
解:由题意得,盲区为,
设,则,
,
解得:,
在大于米小于米的范围内小丽看不见.
故答案为:大于米小于米.
先判断出盲区,然后利用解直角三角形的知识求出盲区即可.
本题考查盲区及解直角三角形的知识,难度不大,关键是找出盲区.
16.【答案】
【解析】
解:由主视图可得长方体的高为,长为,
由俯视图可得宽为,
则左视图的面积为;
故答案为:.
根据主视图可得到长方体的长和高,俯视图可得到长方体的宽,左视图表现长方体的宽和高,让宽高即为左视图的面积.
此题考查了由三视图判断几何体,根据其他视图得到几何体的长和高是解决本题的关键.
17.【答案】
【解析】
【分析】
本题考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”是解题的关键.利用主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而判断图形形状,即可得出小正方体的个数.
【解答】
解:综合三视图,我们可以得出,这个几何模型的底层有个小正方体,第二层有个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是个.
这个几何体的表面积是,
故答案为.
18.【答案】
【解析】
解:过作于,交于,,,
三角形中,::,
因此三角形中,
因此,因此盲区的范围在.
如图,本题所求的就是的值,过作于,交于,利用三角函数可求出.
利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
19.【答案】
【解析】
解:由主视图可知,搭成的几何体有三层,且有列;由左视图可知,搭成的几何体共有行;
第一层有个正方体,第二层有个正方体,第三层有个正方体,
共有个正方体,
搭在这个几何体的基础上添加相同大小的小正方体,以搭成一个大长方体,
搭成的大长方体的共有个小正方体,
至少还需要个小正方体.
故答案为:.
先由主视图、左视图、俯视图求出原来的几何体共有个正方体,再根据搭成的大长方体的共有个小正方体,即可得出答案.
本题考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查,关键是求出搭成的大长方体共有多少个小正方体.
20.【答案】
解:如图,小明的活动区域是、、三个阴影部分区域.
【解析】
根据题意用阴影部分表示出小明的活动区域,,即可.
本题考查作图应用与设计作图,解题的关键是理解题意,灵活运用所学知识解决问题.
21.【答案】
解:如图:连接、并延长交与点,点即为点光源,为旗杆的影子.
【解析】
首先根据小明的身高和影长与树的高度和影长确定点光源,然后由过点光源和旗杆的顶部确定旗杆的影长即可.
本题考查了中心投影的知识,中心投影是由点光源发出的,确定了点光源是解决本题的关键.
22.【答案】
解:阴影部分、为亮亮活动的范围.
【解析】
亮亮活动的安全范围其实就是明明的盲区,因此画亮亮的活动范围只要画出明明的盲区就行了.
本题是结合实际问题来考查学生对视点,视角和盲区的理解能力.
23.【答案】
解:因为汽车司机的视线在车前车后有看不见的地方,即盲区.
汽车前进或倒退时,在车前或车后走很容易出危险.
【解析】
根据汽车司机的视线在车前车后有看不见的地方,很容易出危险,得出坐公共汽车下车后,不要从车前车后猛跑.
此题主要考查了视点、视角和盲区,根据汽车司机的视线在车前车后有盲区进而得出答案是解题关键.
24.【答案】
解:一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为,的矩形,
当圆柱底面圆的半径为,高为,
则圆柱的表面积为:,
体积为:;
当圆柱底面圆的半径为,高为
则圆柱的表面积为:,
体积为:
【解析】
根据平行投影的性质得出当圆柱底面圆的半径为,高为,当圆柱底面圆的半径为,高为,进而分别求出其表面积和体积即可.
此题主要考查了平行投影以及圆柱体的体积公式与表面积公式,得出圆柱体的底面圆的半径结合分类讨论求出答案是解题关键.
25.【答案】
左视图与主视图形状相同,有作垂线直角的痕迹作法不唯一.
两个底面积:;
侧面积:;
表面积:
【解析】
由削去了占底面圆的四分之一部分的柱体易得主视图和左视图相同,可先画一条线段等于主视图中大长方形的长,然后分别做两个端点的垂线及线段的垂直平分线,在两端点的垂线上分别截取主视图的高连接即可得到几何体的左视图;
此零件的表面积两个底面积侧面积,把相关数值代入即可求解.
解决本题的关键是得到零件全面积的等量关系,注意侧面积的展开图应为一个长方形,长方形的长为四分之三圆的周长半径长.
26.【答案】
解:当时,在中,
,
,
即楼房的高度约为米;
当时,小猫不能再晒到太阳,
理由如下:假设没有台阶,当时,从点射下的光线与地面交于点,此时的影长,
设的延长线交于点,
,,
,
设直线与交于点,则,
,
点在上,
大楼的影子落在这个侧面上,
小猫不能晒到太阳.
【解析】
在中,由,即可求出,进而得出答案;
假设没有台阶,当时,从点射下的光线与地面的交点为点,与的交点为点,由,可得,进而判断即可.
本题考查了解直角三角形的应用,锐角三角函数定义,理解题意,将实际问题转化为数学问题是解题的关键.
第2页,共2页
第1页,共1页
