青岛版八年级数学下册 11.2 图形的旋转(2)学案(无答案)
文档属性
| 名称 | 青岛版八年级数学下册 11.2 图形的旋转(2)学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 104.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览


文档简介
11.2 图形的旋转(2)
一、导入激学:
如图:△ABC与△DBE都是等腰直角三角形,∠ACB与∠E都是直角,若△ABC经过旋转后能与△DBE重合,那么旋转中心是点 ,旋转方向是 ,旋转了 度。由复习旧知识导入新课。
二、导标引学
学习目标:
1、运用旋转的基本性质解决有关图形变化问题。
2、能探索发现几何图形的位置发生变化时可能存在的某些不变的量和不变的数量关系,应用这些数量关系解决数学问题。
学习重难点:
运用旋转的基本性质推理和计算及应用旋转中不变的量和不变的数量关系解决数学问题。
三、学习过程
(一)导预疑学
请你利用10分钟,阅读课本,自己按要求完成下列任务,讨论后找出疑难问题。
1.预学核心问题:
(1)如何利用旋转的基本性质进行推理和计算?
(2)当几何图形的位置发生变化时,如何找某些不变的量和不变的数量关系?
2.预学检测:
(1)如右图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在平面上可以作为旋转中心的点共有 个,分别是 .
(2)如下图,点P是正方形ABCD内一点,△ABP经过旋转后与△CBQ重合,且BP=1.
(1)写出旋转中心和旋转角.
(2)∠PBQ= ,PQ= .
(3)连接PQ,判定△BPQ的形状.
3.预学评价质疑
通过预学,你学会了什么?还有什么疑问没有解决呢?请把它们写下来小组交流。
(二)导问互学
问题一:从小组提出的问题中概括出来的核心问题是:
师生设计的活动是:
问题二:运用旋转的基本性质解决数学中的问题
活动1:请同学们自己设计一个绕一点旋转60°后与自身重合的图形。
活动2:学生动手操作课本实验与探究(1),在本子上画出11—26图①,将一直角三角尺按要求放置,小组合作,实验与探究(3)、(4)中的问题,找出其中的等量关系,并证明。
解决问题评价:你在解决问题时在哪里遇到了困难?此类问题今后怎么处理?
(三)导根典学
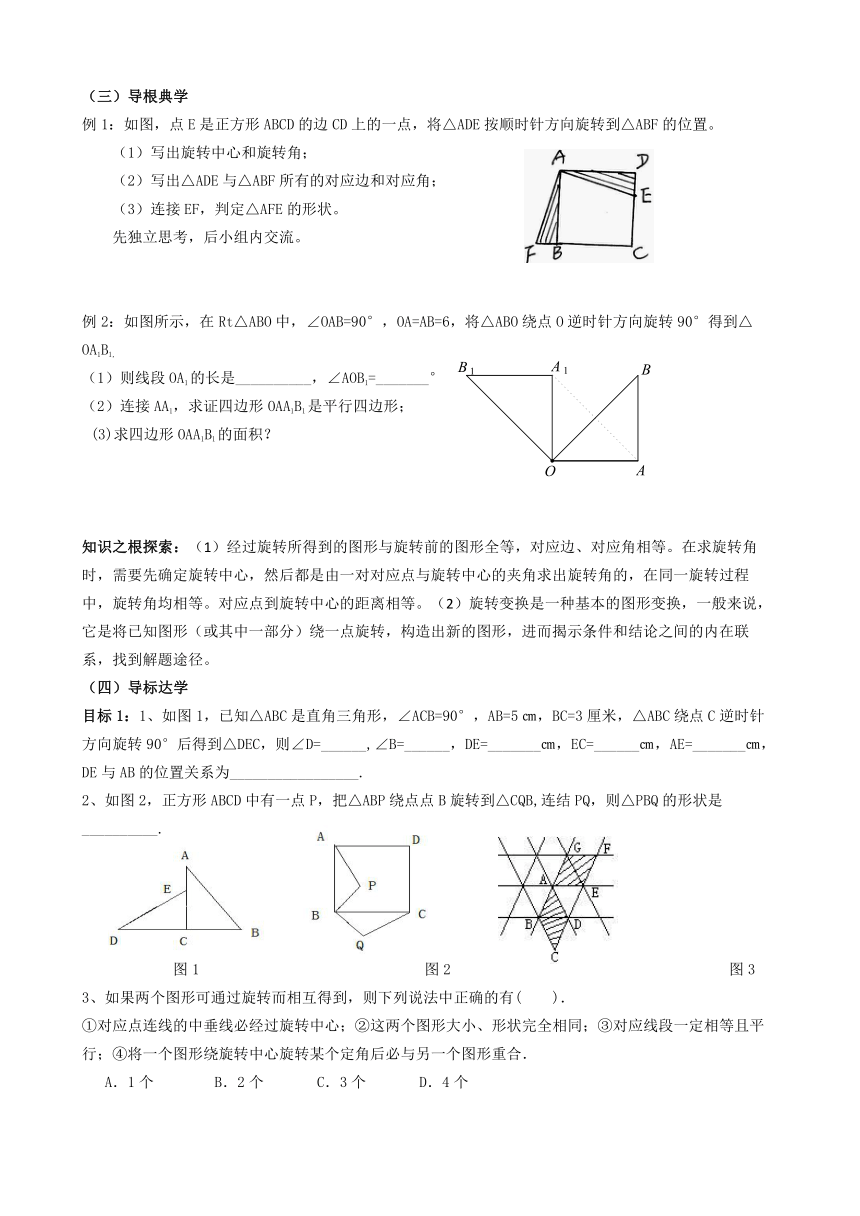
例1:如图,点E是正方形ABCD的边CD上的一点,将△ADE按顺时针方向旋转到△ABF的位置。
(1)写出旋转中心和旋转角;
(2)写出△ADE与△ABF所有的对应边和对应角;
(3)连接EF,判定△AFE的形状。
先独立思考,后小组内交流。
例2:如图所示,在Rt△ABO中,∠OAB=90°,OA=AB=6,将△ABO绕点O逆时针方向旋转90°得到△OA1B1,
(1)则线段OA1的长是__________,∠AOB1=_______°
(2)连接AA1,求证四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积?
知识之根探索:(1)经过旋转所得到的图形与旋转前的图形全等,对应边、对应角相等。在求旋转角时,需要先确定旋转中心,然后都是由一对对应点与旋转中心的夹角求出旋转角的,在同一旋转过程中,旋转角均相等。对应点到旋转中心的距离相等。(2)旋转变换是一种基本的图形变换,一般来说,它是将已知图形(或其中一部分)绕一点旋转,构造出新的图形,进而揭示条件和结论之间的内在联系,找到解题途径。
(四)导标达学
目标1:1、如图1,已知△ABC是直角三角形,∠ACB=90°,AB=5㎝,BC=3厘米,△ABC绕点C逆时针方向旋转90°后得到△DEC,则∠D=______,∠B=______,DE=_______㎝,EC=______㎝,AE=_______㎝,DE与AB的位置关系为_________________.
2、如图2,正方形ABCD中有一点P,把△ABP绕点点B旋转到△CQB,连结PQ,则△PBQ的形状是__________.
图1 图2 图3
3、如果两个图形可通过旋转而相互得到,则下列说法中正确的有( ).
①对应点连线的中垂线必经过旋转中心;②这两个图形大小、形状完全相同;③对应线段一定相等且平行;④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.
A.1个 B.2个 C.3个 D.4个
4、如图3,同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,其中菱形AEFG可以看成是把菱形ABCD以A为中心( ).
A.顺时针旋转60°得到 B.顺时针旋转120°得到
C.逆时针旋转60°得到 D.逆时针旋转120°得到
5、如图,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是( ).
6如图1,O是等边△ABC内一点,将△AOB绕A点逆时针旋转,使得B、O两点的对应点分别为C、D,则旋转角为_______,图中除△ABC外,还有________是等边三角形。
目标2:7、如图2所示,△ABC是等腰直角三角形,BC是斜边,P是△ABC内一点,将△ABP绕点A逆时针旋转后于△ACQ重合,如果AP=3,则PQ=__________。
(
O
M
B
A
图4
)图1 图2
图3
8、如图3,△ABC绕着点C顺时针旋转35°得到△C ,若⊥AC,则∠A的度数是 。
9、如图4用等腰直角三角板画,并将三角板沿方向平移到如图所示的虚线处后绕点逆时针方向旋转,则三角板的斜边与射线的夹角为_____。
10.如图5,边长为3的正方形ABCD绕点C 按顺时针方向旋转30°后得到的正方形EFCG,EF 交AD于点H,那么DH 的长为______。
11.如图6,将矩形ABCD绕点A顺时针旋转90゜后,得到矩形AB′C ′D′,如果CD=2DA=2,那么CC′=_________。
图5 图6 图 7
综合提升(选做):
1、如图7,四边形ABCD的∠BAD=∠C=90°,AB =AD ,AE⊥ BC 于E,
△BEA旋转一定角度后能与△DFA重合.
旋转中心是哪一点?
旋转了多少度?
若AE=5cm,求四边形ABCD的面积.
(
D
C
A
B
G
H
F
E
)
把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,
边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?
请先观察猜想,然后再证明你的猜想.
3.在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.
(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.
反馈评价:请交流你发现的问题,并把它们进行更正。
四、导法慧学
1.将所学知识纳入知识体系.
2.本节解决问题的具体方法是怎样的?据此请总结此类问题的解题思路.
3.还有没有更好的解法?你还有疑问吗?
一、导入激学:
如图:△ABC与△DBE都是等腰直角三角形,∠ACB与∠E都是直角,若△ABC经过旋转后能与△DBE重合,那么旋转中心是点 ,旋转方向是 ,旋转了 度。由复习旧知识导入新课。
二、导标引学
学习目标:
1、运用旋转的基本性质解决有关图形变化问题。
2、能探索发现几何图形的位置发生变化时可能存在的某些不变的量和不变的数量关系,应用这些数量关系解决数学问题。
学习重难点:
运用旋转的基本性质推理和计算及应用旋转中不变的量和不变的数量关系解决数学问题。
三、学习过程
(一)导预疑学
请你利用10分钟,阅读课本,自己按要求完成下列任务,讨论后找出疑难问题。
1.预学核心问题:
(1)如何利用旋转的基本性质进行推理和计算?
(2)当几何图形的位置发生变化时,如何找某些不变的量和不变的数量关系?
2.预学检测:
(1)如右图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在平面上可以作为旋转中心的点共有 个,分别是 .
(2)如下图,点P是正方形ABCD内一点,△ABP经过旋转后与△CBQ重合,且BP=1.
(1)写出旋转中心和旋转角.
(2)∠PBQ= ,PQ= .
(3)连接PQ,判定△BPQ的形状.
3.预学评价质疑
通过预学,你学会了什么?还有什么疑问没有解决呢?请把它们写下来小组交流。
(二)导问互学
问题一:从小组提出的问题中概括出来的核心问题是:
师生设计的活动是:
问题二:运用旋转的基本性质解决数学中的问题
活动1:请同学们自己设计一个绕一点旋转60°后与自身重合的图形。
活动2:学生动手操作课本实验与探究(1),在本子上画出11—26图①,将一直角三角尺按要求放置,小组合作,实验与探究(3)、(4)中的问题,找出其中的等量关系,并证明。
解决问题评价:你在解决问题时在哪里遇到了困难?此类问题今后怎么处理?
(三)导根典学
例1:如图,点E是正方形ABCD的边CD上的一点,将△ADE按顺时针方向旋转到△ABF的位置。
(1)写出旋转中心和旋转角;
(2)写出△ADE与△ABF所有的对应边和对应角;
(3)连接EF,判定△AFE的形状。
先独立思考,后小组内交流。
例2:如图所示,在Rt△ABO中,∠OAB=90°,OA=AB=6,将△ABO绕点O逆时针方向旋转90°得到△OA1B1,
(1)则线段OA1的长是__________,∠AOB1=_______°
(2)连接AA1,求证四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积?
知识之根探索:(1)经过旋转所得到的图形与旋转前的图形全等,对应边、对应角相等。在求旋转角时,需要先确定旋转中心,然后都是由一对对应点与旋转中心的夹角求出旋转角的,在同一旋转过程中,旋转角均相等。对应点到旋转中心的距离相等。(2)旋转变换是一种基本的图形变换,一般来说,它是将已知图形(或其中一部分)绕一点旋转,构造出新的图形,进而揭示条件和结论之间的内在联系,找到解题途径。
(四)导标达学
目标1:1、如图1,已知△ABC是直角三角形,∠ACB=90°,AB=5㎝,BC=3厘米,△ABC绕点C逆时针方向旋转90°后得到△DEC,则∠D=______,∠B=______,DE=_______㎝,EC=______㎝,AE=_______㎝,DE与AB的位置关系为_________________.
2、如图2,正方形ABCD中有一点P,把△ABP绕点点B旋转到△CQB,连结PQ,则△PBQ的形状是__________.
图1 图2 图3
3、如果两个图形可通过旋转而相互得到,则下列说法中正确的有( ).
①对应点连线的中垂线必经过旋转中心;②这两个图形大小、形状完全相同;③对应线段一定相等且平行;④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.
A.1个 B.2个 C.3个 D.4个
4、如图3,同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,其中菱形AEFG可以看成是把菱形ABCD以A为中心( ).
A.顺时针旋转60°得到 B.顺时针旋转120°得到
C.逆时针旋转60°得到 D.逆时针旋转120°得到
5、如图,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是( ).
6如图1,O是等边△ABC内一点,将△AOB绕A点逆时针旋转,使得B、O两点的对应点分别为C、D,则旋转角为_______,图中除△ABC外,还有________是等边三角形。
目标2:7、如图2所示,△ABC是等腰直角三角形,BC是斜边,P是△ABC内一点,将△ABP绕点A逆时针旋转后于△ACQ重合,如果AP=3,则PQ=__________。
(
O
M
B
A
图4
)图1 图2
图3
8、如图3,△ABC绕着点C顺时针旋转35°得到△C ,若⊥AC,则∠A的度数是 。
9、如图4用等腰直角三角板画,并将三角板沿方向平移到如图所示的虚线处后绕点逆时针方向旋转,则三角板的斜边与射线的夹角为_____。
10.如图5,边长为3的正方形ABCD绕点C 按顺时针方向旋转30°后得到的正方形EFCG,EF 交AD于点H,那么DH 的长为______。
11.如图6,将矩形ABCD绕点A顺时针旋转90゜后,得到矩形AB′C ′D′,如果CD=2DA=2,那么CC′=_________。
图5 图6 图 7
综合提升(选做):
1、如图7,四边形ABCD的∠BAD=∠C=90°,AB =AD ,AE⊥ BC 于E,
△BEA旋转一定角度后能与△DFA重合.
旋转中心是哪一点?
旋转了多少度?
若AE=5cm,求四边形ABCD的面积.
(
D
C
A
B
G
H
F
E
)
把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,
边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?
请先观察猜想,然后再证明你的猜想.
3.在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.
(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.
反馈评价:请交流你发现的问题,并把它们进行更正。
四、导法慧学
1.将所学知识纳入知识体系.
2.本节解决问题的具体方法是怎样的?据此请总结此类问题的解题思路.
3.还有没有更好的解法?你还有疑问吗?
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
