沪科版数学七年级下册 7.4 综合与实践 排队问题 教案
文档属性
| 名称 | 沪科版数学七年级下册 7.4 综合与实践 排队问题 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 211.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 17:16:51 | ||
图片预览

文档简介
教学设计
教学目标
知识与技能
1、经历观察、操作、归纳、推理等实践活动,培养学生的认知能力。
2、在探索问题的过程中使学生感受数学在日常生活中的广泛应用。
过程与方法
初步学会在具体情境中从数学的角度发现和提出问题,总结规律并综合运用所学数学知识和方法等解决简单的实际问题,增强应用意识,提高实践能力。
情感、态度与价值观
积累数学活动经验、培养学生应用意识和创新意识。
教学重难点
重点:在实际问题中发现和总结规律
难点:规律结过程
教学过程
一、创设情境
师:通过每个月的11日为排队推动日来引导出今天的主题
同学们,日常生活中我们排过哪些队?
生:买票、打饭、医院挂号、银行办理业务……
师:是的,在我们日常生活中有很多事情需要排队依次进行,除了上述有形的排队,还有大量“无形”的排队现象,例如,生产线上的原料等待加工,因故障停止运行的机器等待工人 维修等。
(出示图片视频)
师:生活中你所见到的排队现象存在着哪些问题?
生:小组交流想法
师:某些场合下,由于排队的人很多,人们将花费很多时间等待,这使人们的工作和生活受到很大影响,同时,也使人们对服务机构的服务产生不满,服务机构通常通过增加服务窗口来减少排队,但窗口增加过多又会造成人力、物力的浪费。
如何使投入的资源较少,而顾客对得到的服务又较满意,这就需要研究排队问题,今天我们就来研究最简单的排队问题。
(出示课题,排队问题)
探究新知
师:多媒体出示问题1:
某服务机构开设了一个窗口办理业务,并按顾客“先到达,先服务”的方式服务,该窗口每2 min服务以为顾客,已知当窗口开始工作时,已有5位顾客在等待,在窗口开始工作1 min后,又有一位“新顾客”到达,且预计以后每5 min都有一位“新顾客”到达。
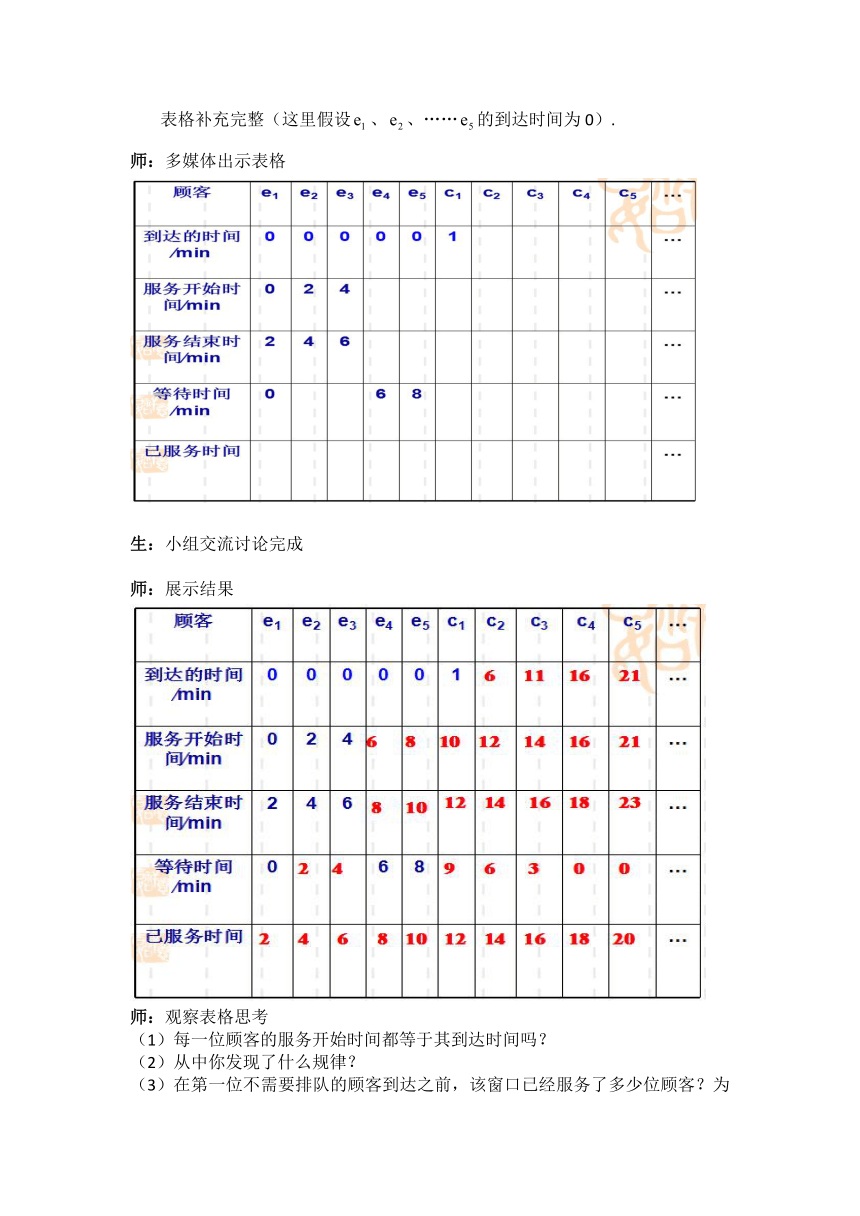
设、、……表示当前窗口开始工作时已经在等待的5位顾客,、、……表示在窗口开始工作以后,按先后到达的“新顾客”,请将下面表格补充完整(这里假设、、……的到达时间为0).
师:多媒体出示表格
生:小组交流讨论完成
师:展示结果
师:观察表格思考
每一位顾客的服务开始时间都等于其到达时间吗?
从中你发现了什么规律?
在第一位不需要排队的顾客到达之前,该窗口已经服务了多少位顾客?为 这些顾客 共花费了多长时间?
平均等待时间是一个重要服务指标,为考察服务质量,问排队现象消失之前 ,所有顾客平均等待时间是多少?
生:指名回答
师:在上述问题中,如果问题的条件变复杂(例如,当窗口开始工作时已经在等待的顾客非常多),使用列表方法就很不方便,你能否用代数式表示出上面的数量,总结上面表格中的数量关系,并根据这个关系来解决问题呢?
多媒体出示问题2:
在问题1的条件中,当服务机构的窗口开始工作时,如果已经有10位顾客在等待(其他条件不变),且当“新顾客”离去时,排队现象就此消失了,即位第一位到达后不需要排队的“新顾客”。
问:
用n的代数式来表示,在第一位不需要排队的“新顾客”到达之前, 该窗口已经服务了多少位顾客?位这些顾客服务共花费了多长时间?
用关于n的代数式来表示的到达时间。
根据(1)和(2)得到的代数式以及他们的数量关系,求n+1的值。
师:引导学生小组讨论交流(1)和(2),合作完成
注意:教师深入到学生中间进行指导
师:小组反馈,集体讲评
出示答案:(1)服务了(n+10)位顾客,花费了2(n+10)=(2n+20)分
(2)5(n+1-1)+1=(5n+1)分
师:思考:在到达服务机构之前,该窗口为顾客服务花费的时间和的到 达时间有怎样的关系?
生:思考后回答
师:小结:在到达服务机构之前,该窗口为顾客服务所花费的时间小于等于的到达时间,学生尝试求(3)
师:出示答案进行校正
解:根据题意得 2(n+10)≤ 5n+1
解得 n ≥
因为为第一位到达后不需要排队的“新顾客”,则n取最小整数值7,则n+1=8
归纳小结
通过本节课的学习,你有什么收获?你认为总结规律的一般方法是什么?
希望同学们在以后的学习中能积极参与数学实践活动中来,主动探索,积极思考,我相信同学们在参与活动的过程中一定会有所收获。
布置作业
以小组为单位选择一个现象进行调查,并就你调查发现的问题设计一个解决方案。
板书设计
创设情境 三、归纳小结
探究新知 四、布置作业
教学目标
知识与技能
1、经历观察、操作、归纳、推理等实践活动,培养学生的认知能力。
2、在探索问题的过程中使学生感受数学在日常生活中的广泛应用。
过程与方法
初步学会在具体情境中从数学的角度发现和提出问题,总结规律并综合运用所学数学知识和方法等解决简单的实际问题,增强应用意识,提高实践能力。
情感、态度与价值观
积累数学活动经验、培养学生应用意识和创新意识。
教学重难点
重点:在实际问题中发现和总结规律
难点:规律结过程
教学过程
一、创设情境
师:通过每个月的11日为排队推动日来引导出今天的主题
同学们,日常生活中我们排过哪些队?
生:买票、打饭、医院挂号、银行办理业务……
师:是的,在我们日常生活中有很多事情需要排队依次进行,除了上述有形的排队,还有大量“无形”的排队现象,例如,生产线上的原料等待加工,因故障停止运行的机器等待工人 维修等。
(出示图片视频)
师:生活中你所见到的排队现象存在着哪些问题?
生:小组交流想法
师:某些场合下,由于排队的人很多,人们将花费很多时间等待,这使人们的工作和生活受到很大影响,同时,也使人们对服务机构的服务产生不满,服务机构通常通过增加服务窗口来减少排队,但窗口增加过多又会造成人力、物力的浪费。
如何使投入的资源较少,而顾客对得到的服务又较满意,这就需要研究排队问题,今天我们就来研究最简单的排队问题。
(出示课题,排队问题)
探究新知
师:多媒体出示问题1:
某服务机构开设了一个窗口办理业务,并按顾客“先到达,先服务”的方式服务,该窗口每2 min服务以为顾客,已知当窗口开始工作时,已有5位顾客在等待,在窗口开始工作1 min后,又有一位“新顾客”到达,且预计以后每5 min都有一位“新顾客”到达。
设、、……表示当前窗口开始工作时已经在等待的5位顾客,、、……表示在窗口开始工作以后,按先后到达的“新顾客”,请将下面表格补充完整(这里假设、、……的到达时间为0).
师:多媒体出示表格
生:小组交流讨论完成
师:展示结果
师:观察表格思考
每一位顾客的服务开始时间都等于其到达时间吗?
从中你发现了什么规律?
在第一位不需要排队的顾客到达之前,该窗口已经服务了多少位顾客?为 这些顾客 共花费了多长时间?
平均等待时间是一个重要服务指标,为考察服务质量,问排队现象消失之前 ,所有顾客平均等待时间是多少?
生:指名回答
师:在上述问题中,如果问题的条件变复杂(例如,当窗口开始工作时已经在等待的顾客非常多),使用列表方法就很不方便,你能否用代数式表示出上面的数量,总结上面表格中的数量关系,并根据这个关系来解决问题呢?
多媒体出示问题2:
在问题1的条件中,当服务机构的窗口开始工作时,如果已经有10位顾客在等待(其他条件不变),且当“新顾客”离去时,排队现象就此消失了,即位第一位到达后不需要排队的“新顾客”。
问:
用n的代数式来表示,在第一位不需要排队的“新顾客”到达之前, 该窗口已经服务了多少位顾客?位这些顾客服务共花费了多长时间?
用关于n的代数式来表示的到达时间。
根据(1)和(2)得到的代数式以及他们的数量关系,求n+1的值。
师:引导学生小组讨论交流(1)和(2),合作完成
注意:教师深入到学生中间进行指导
师:小组反馈,集体讲评
出示答案:(1)服务了(n+10)位顾客,花费了2(n+10)=(2n+20)分
(2)5(n+1-1)+1=(5n+1)分
师:思考:在到达服务机构之前,该窗口为顾客服务花费的时间和的到 达时间有怎样的关系?
生:思考后回答
师:小结:在到达服务机构之前,该窗口为顾客服务所花费的时间小于等于的到达时间,学生尝试求(3)
师:出示答案进行校正
解:根据题意得 2(n+10)≤ 5n+1
解得 n ≥
因为为第一位到达后不需要排队的“新顾客”,则n取最小整数值7,则n+1=8
归纳小结
通过本节课的学习,你有什么收获?你认为总结规律的一般方法是什么?
希望同学们在以后的学习中能积极参与数学实践活动中来,主动探索,积极思考,我相信同学们在参与活动的过程中一定会有所收获。
布置作业
以小组为单位选择一个现象进行调查,并就你调查发现的问题设计一个解决方案。
板书设计
创设情境 三、归纳小结
探究新知 四、布置作业
