2022届高考数学三轮冲刺课之解答题2 立体几何课件(共41张PPT)
文档属性
| 名称 | 2022届高考数学三轮冲刺课之解答题2 立体几何课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 14:58:39 | ||
图片预览








文档简介
(共41张PPT)
高考数学冲刺之解答题2
立体几何
主讲人: |
2
01
解答题
三角函数与解三角形
02
解答题
立体几何
03
解答题
统计与概率
04
解答题
函数与导数
05
解答题
极坐标与参数方程
3
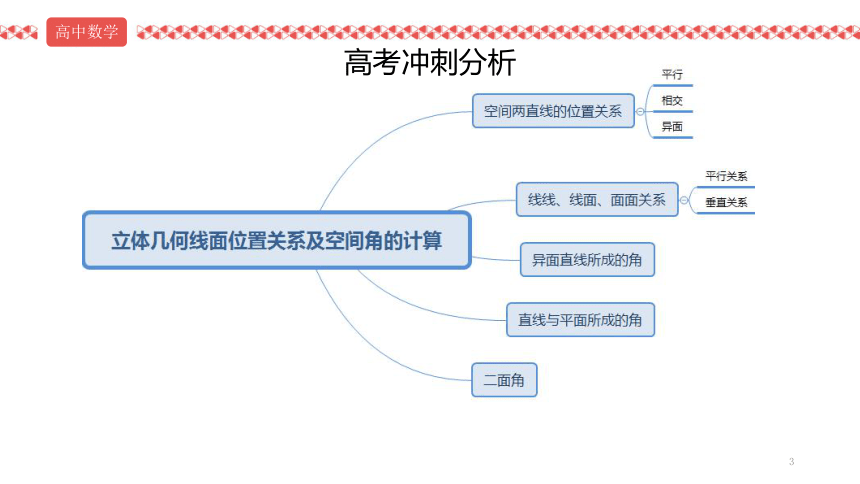
高考冲刺分析
4
高考冲刺分析
立体几何高考解答题常以棱柱或者棱锥为载体,一般设置两问。
“一证一算”,一问是定性分析,一问是定量分析。其中定性分析以线、面平行、垂直的证明为主。考查逻辑推理能力及学科素养;而定量分析主要是应用空间向量求线面角、二面角,考查数学运算能力与学科素养。
5
本节说明
立体几何:
类型一:线面平行 类型二:线面垂直 类型三:线面夹角 类型四:面面夹角
题型专练1
题型专练2
题型专练3
题型专练4
6
题型专练1
难度及考查内容:
1. 难度:以基础、中等题为主.
2.考查内容:
(1) 直线与平面平行的判定
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
简记为:线线平行,则线面平行.
符号表示:
(2)平面与平面的判定
两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行.
例题
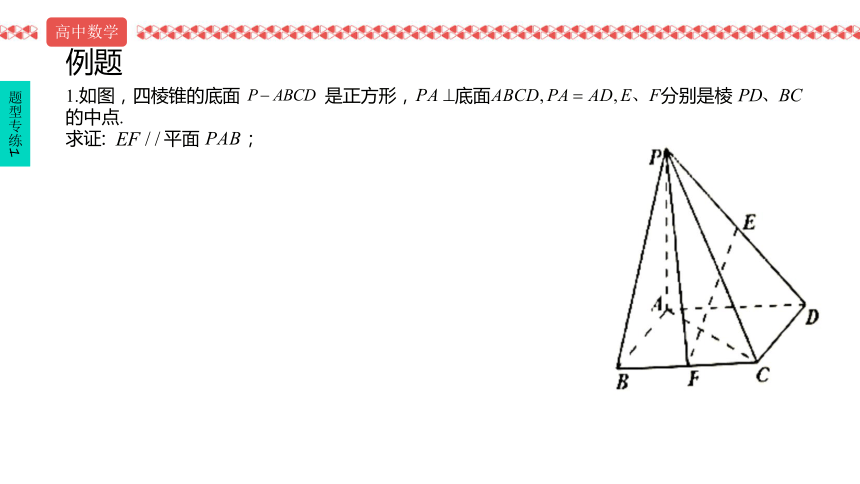
1.如图,四棱锥的底面 是正方形, 底面 分别是棱 的中点.
求证: 平面 ;
题型专练1
例题
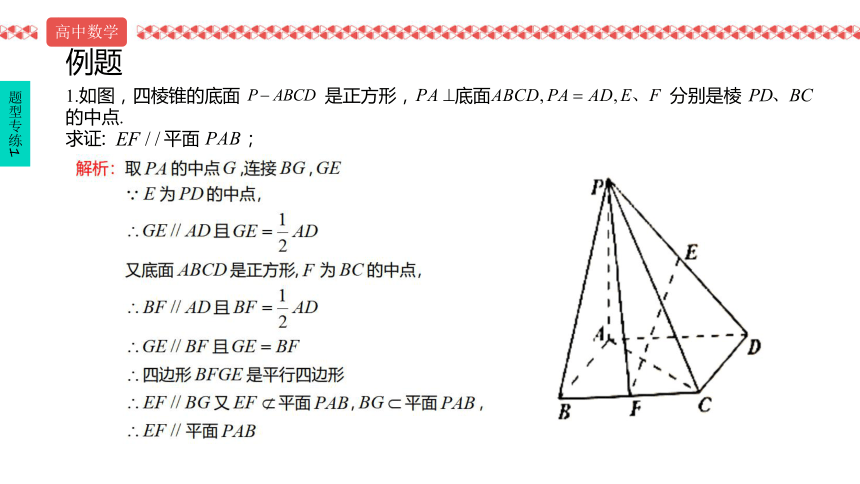
1.如图,四棱锥的底面 是正方形, 底面 分别是棱 的中点.
求证: 平面 ;
题型专练1
线面平行解题模板:
第一步:作辅助线,构造相似三角形或者平面四边形,如.
第二步:线线平行,且一条直线不在面内,推出线面平行.
题型专练1
10
难度及考查内容:
1. 难度:以基础、中等题为主.
2.考查内容:
(1) 直线与平面垂直的判定
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
注意:
①定理中的“两条相交直线”这一条件不可忽视;
②定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.
(2)平面与平面垂直的判定
一个平面过另一个平面的垂线,则这两个平面垂直.
题型专练2
例题
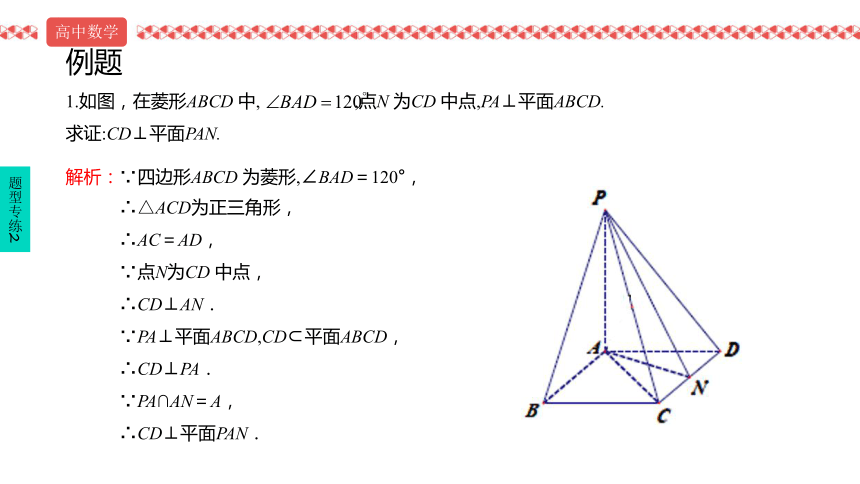
1.如图,在菱形ABCD 中, ,点N 为CD 中点,PA⊥平面ABCD.
求证:CD⊥平面PAN.
题型专练2
例题
1.如图,在菱形ABCD 中, ,点N 为CD 中点,PA⊥平面ABCD.
求证:CD⊥平面PAN.
解析:∵四边形ABCD 为菱形,∠BAD=120°,
∴△ACD为正三角形,
∴AC=AD,
∵点N为CD 中点,
∴CD⊥AN.
∵PA⊥平面ABCD,CD 平面ABCD,
∴CD⊥PA.
∵PA∩AN=A,
∴CD⊥平面PAN.
题型专练2
例题
题型专练2
例题
题型专练2
线面垂直解题模板:
第一步:证明线垂直于面内一条直线
第二步:证明线垂直于面内另一条直线
第三步:平面内两条直线相交于一点
第四步:线垂直于平面
题型专练2
练习
题型专练2
练习
题型专练2
18
难度及考查内容:
1. 难度:以基础、中等题为主.
2.考查内容:
(1) 平面法向量
题型专练3
19
难度及考查内容:
(2)线面夹角
题型专练3
例题
例题
题型专练3
例题
例题
题型专练3
例题
例题
题型专练3
题型专练3
线面夹角解题模板:
第一步:建立空间直角坐标系,建系时,尽可能利用棱柱或棱锥的垂直关系;
第二步:求出相关点的坐标,表示出面内相交向量的坐标
第三步:线面夹角:结合公式,线与面法向量的夹角为锐角,求出的是夹角正弦值。
第四步:转化为几何结论。
练习
题型专练3
练习
题型专练3
练习
题型专练3
练习
题型专练3
练习
题型专练3
29
难度及考查内容:
1. 难度:以基础、中等题为主.
2.考查内容:
题型专练4
例题
例题
题型专练4
例题
例题
题型专练4
面面夹角解题模板:
第一步:建立空间直角坐标系,建系时,尽可能利用棱柱或棱锥的垂直关系;
第二步:求出相关点的坐标,表示出面内相交向量的坐标
第三步:面面夹角:结合公式,两个面的法向量的夹角与二面角的大小是相等或者互补的(根据具体情况判断)
第四步:转化为几何结论。
题型专练4
练习
题型专练4
练习
题型专练4
练习
题型专练4
练习
题型专练4
练习
题型专练4
练习
题型专练4
高考状元满分心得:
1.解题指导:仔细审题,画出关键词
2.建系规则:尽量使各个点都落在坐标轴上.
3.求点的坐标技巧:一是转化为平面图形; 二是利用向量共线.
4.已知条件的意图:
(1)已知边长有两个作用,一是方便建系设点的坐标;二是利用勾股定理证明垂直. (2)已知面面垂直的作用:证明线面垂直.
5.线面平行的证明:法1:线线平行;法2:面面平行
温馨提示:有些时候法向量就是坐标轴.
当堂总结
线面平行解题模板:
第一步:作辅助线,构造相似三角形或者平面四边形
第二步:线线平行,且一条直线不在面内,推出线面平行
线面垂直解题模板:
第一步:证明线垂直于面内一条直线
第二步:证明线垂直于面内另一条直线
第三步:平面内两条直线相交于一点
第四步:线垂直于平面
当堂总结
面面夹角解题模板:
第一步:建立空间直角坐标系,建系时,尽可能利用棱柱或棱锥的垂直关系;
第二步:求出相关点的坐标,表示出面内相交向量的坐标
第三步:面面夹角:结合公式,两个面的法向量的夹角与二面角的大小是相等
或者互补的(根据具体情况判断)
第四步:转化为几何结论。
线面夹角解题模板:
第一步:建立空间直角坐标系,建系时,尽可能利用棱柱或棱锥的垂直关系;
第二步:求出相关点的坐标,表示出面内相交向量的坐标
第三步:线面夹角:结合公式,线与面法向量的夹角为锐角,求出的是夹角
正弦值。
第四步:转化为几何结论。
高考数学冲刺之解答题2
立体几何
主讲人: |
2
01
解答题
三角函数与解三角形
02
解答题
立体几何
03
解答题
统计与概率
04
解答题
函数与导数
05
解答题
极坐标与参数方程
3
高考冲刺分析
4
高考冲刺分析
立体几何高考解答题常以棱柱或者棱锥为载体,一般设置两问。
“一证一算”,一问是定性分析,一问是定量分析。其中定性分析以线、面平行、垂直的证明为主。考查逻辑推理能力及学科素养;而定量分析主要是应用空间向量求线面角、二面角,考查数学运算能力与学科素养。
5
本节说明
立体几何:
类型一:线面平行 类型二:线面垂直 类型三:线面夹角 类型四:面面夹角
题型专练1
题型专练2
题型专练3
题型专练4
6
题型专练1
难度及考查内容:
1. 难度:以基础、中等题为主.
2.考查内容:
(1) 直线与平面平行的判定
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
简记为:线线平行,则线面平行.
符号表示:
(2)平面与平面的判定
两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行.
例题
1.如图,四棱锥的底面 是正方形, 底面 分别是棱 的中点.
求证: 平面 ;
题型专练1
例题
1.如图,四棱锥的底面 是正方形, 底面 分别是棱 的中点.
求证: 平面 ;
题型专练1
线面平行解题模板:
第一步:作辅助线,构造相似三角形或者平面四边形,如.
第二步:线线平行,且一条直线不在面内,推出线面平行.
题型专练1
10
难度及考查内容:
1. 难度:以基础、中等题为主.
2.考查内容:
(1) 直线与平面垂直的判定
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
注意:
①定理中的“两条相交直线”这一条件不可忽视;
②定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.
(2)平面与平面垂直的判定
一个平面过另一个平面的垂线,则这两个平面垂直.
题型专练2
例题
1.如图,在菱形ABCD 中, ,点N 为CD 中点,PA⊥平面ABCD.
求证:CD⊥平面PAN.
题型专练2
例题
1.如图,在菱形ABCD 中, ,点N 为CD 中点,PA⊥平面ABCD.
求证:CD⊥平面PAN.
解析:∵四边形ABCD 为菱形,∠BAD=120°,
∴△ACD为正三角形,
∴AC=AD,
∵点N为CD 中点,
∴CD⊥AN.
∵PA⊥平面ABCD,CD 平面ABCD,
∴CD⊥PA.
∵PA∩AN=A,
∴CD⊥平面PAN.
题型专练2
例题
题型专练2
例题
题型专练2
线面垂直解题模板:
第一步:证明线垂直于面内一条直线
第二步:证明线垂直于面内另一条直线
第三步:平面内两条直线相交于一点
第四步:线垂直于平面
题型专练2
练习
题型专练2
练习
题型专练2
18
难度及考查内容:
1. 难度:以基础、中等题为主.
2.考查内容:
(1) 平面法向量
题型专练3
19
难度及考查内容:
(2)线面夹角
题型专练3
例题
例题
题型专练3
例题
例题
题型专练3
例题
例题
题型专练3
题型专练3
线面夹角解题模板:
第一步:建立空间直角坐标系,建系时,尽可能利用棱柱或棱锥的垂直关系;
第二步:求出相关点的坐标,表示出面内相交向量的坐标
第三步:线面夹角:结合公式,线与面法向量的夹角为锐角,求出的是夹角正弦值。
第四步:转化为几何结论。
练习
题型专练3
练习
题型专练3
练习
题型专练3
练习
题型专练3
练习
题型专练3
29
难度及考查内容:
1. 难度:以基础、中等题为主.
2.考查内容:
题型专练4
例题
例题
题型专练4
例题
例题
题型专练4
面面夹角解题模板:
第一步:建立空间直角坐标系,建系时,尽可能利用棱柱或棱锥的垂直关系;
第二步:求出相关点的坐标,表示出面内相交向量的坐标
第三步:面面夹角:结合公式,两个面的法向量的夹角与二面角的大小是相等或者互补的(根据具体情况判断)
第四步:转化为几何结论。
题型专练4
练习
题型专练4
练习
题型专练4
练习
题型专练4
练习
题型专练4
练习
题型专练4
练习
题型专练4
高考状元满分心得:
1.解题指导:仔细审题,画出关键词
2.建系规则:尽量使各个点都落在坐标轴上.
3.求点的坐标技巧:一是转化为平面图形; 二是利用向量共线.
4.已知条件的意图:
(1)已知边长有两个作用,一是方便建系设点的坐标;二是利用勾股定理证明垂直. (2)已知面面垂直的作用:证明线面垂直.
5.线面平行的证明:法1:线线平行;法2:面面平行
温馨提示:有些时候法向量就是坐标轴.
当堂总结
线面平行解题模板:
第一步:作辅助线,构造相似三角形或者平面四边形
第二步:线线平行,且一条直线不在面内,推出线面平行
线面垂直解题模板:
第一步:证明线垂直于面内一条直线
第二步:证明线垂直于面内另一条直线
第三步:平面内两条直线相交于一点
第四步:线垂直于平面
当堂总结
面面夹角解题模板:
第一步:建立空间直角坐标系,建系时,尽可能利用棱柱或棱锥的垂直关系;
第二步:求出相关点的坐标,表示出面内相交向量的坐标
第三步:面面夹角:结合公式,两个面的法向量的夹角与二面角的大小是相等
或者互补的(根据具体情况判断)
第四步:转化为几何结论。
线面夹角解题模板:
第一步:建立空间直角坐标系,建系时,尽可能利用棱柱或棱锥的垂直关系;
第二步:求出相关点的坐标,表示出面内相交向量的坐标
第三步:线面夹角:结合公式,线与面法向量的夹角为锐角,求出的是夹角
正弦值。
第四步:转化为几何结论。
同课章节目录
