2022届高考数学三轮冲刺课之解答题3 统计与概率课件(共50张PPT)
文档属性
| 名称 | 2022届高考数学三轮冲刺课之解答题3 统计与概率课件(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 20:20:11 | ||
图片预览











文档简介
(共50张PPT)
高考数学冲刺之解答题3
统计与概率
主讲人: |
2
01
解答题
三角函数与解三角形
02
解答题
立体几何
03
解答题
统计与概率
04
解答题
函数与导数
05
解答题
极坐标与参数方程
3
高考说明
近几年统计与概率问题主要以现实生活、古代文化为背景来考查统计图表的识别,排列与组合与古典概型的交汇,二项式定理,几何概型,双图(茎叶图、频率直方图)与离散型随机变量的分布列,统计案例相结合等,呈现考点模式化与考题应用化的特点,难度中等,题目为两小一大,分值在17到20分左右.
4
解答题的命题特点
(一)用定义法求解离散型随机变量的分布列,试题难度中等,综合考查排列组合知识和与互斥事件、对立事件以及相互独立事件的有关应用.
(二) 概型法求解随机变量的分布列的应用问题,试题难度中等,综合考查二项分布、正态分布、超几何分布等特殊分布和概率、统计知识的应用.
(三)公式法和比例法求解样本估计总体问题,试题难度中等,综合考查概率、抽样方法、统计图表、样本的数字特征的应用.
(四)模型法求解统计案例的问题,试题难度中等,综合考查概率统计与线性回归、独立性检验知识的应用.
(五)通过概率统计与函数、数列等知识的综合应用,综合考查概率统计在实际生活中的决策作用,试题难度较大.
5
本节说明
统计与概率:
类型一:变量间的相关关系 类型二:独立性检验
类型三:随机变量及其分布 类型四:统计与概率的综合
题型专练1
题型专练2
题型专练3
题型专练4
6
回归直线 经过样本点的中心 ,若x取某一个值代入回归直线方程
中,可求出y的估计值.
1.求回归直线方程的关键及实际应用:
(1)关键:正确理解 的计算公式和准确地计算.
(2)实际应用:在分析实际中两个变量的相关关系时,可根据样本数据作出散点图来确定两个
变量之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程估计和预测变
量的值.
2.相关系数:
(1)当r>0时,表明两个变量正相关;当r<0时,两个变量负相关.
(2)当|r|>0.75时,认为两个变量具有较强的线性相关关系.
题型专练1
7
例题
1. (安徽模拟)有一种速度叫中国速度,有一种骄傲叫中国高铁.中国高铁经过十几年的发展,取得了举世瞩目的成就,使我国完成了从较落后向先进铁路国的跨越式转变.中国的高铁技术不但越来越成熟,而且还走向国外,帮助不少国家修建了高铁.高铁可以说是中国一张行走的名片.截至到2020年,中国高铁运营里程已经达到3.9万公里.如表是2013年至2020年中国高铁每年的运营里程统计表,它反映了中国高铁近几年的飞速发展:
根据以上数据,回答下面问题.
(1)甲同学用曲线y=bx+a来拟合,并算得相关系数r1=0.97,乙同学用曲线y=cedx来拟合,并算得转化为线性回归方程所对应的相关系数r2=0.99,试问哪一个更适合作为y关于x的回归方程类型,并说明理由;
年份 2013 2014 2015 2016 2017 2018 2019 2020
年份代码x 1 2 3 4 5 6 7 8
运营里程y(万公里) 1.3 1.6 1.9 2.2 2.5 2.9 3.5 3.9
题型专练1
8
例题
(2)根据(1)的判断结果及表中数据,求y关于x的回归方程(系数精确到0.01).
参考公式:用最小二乘法求线性回归方程的系数公式:
题型专练1
9
例题
题型专练1
10
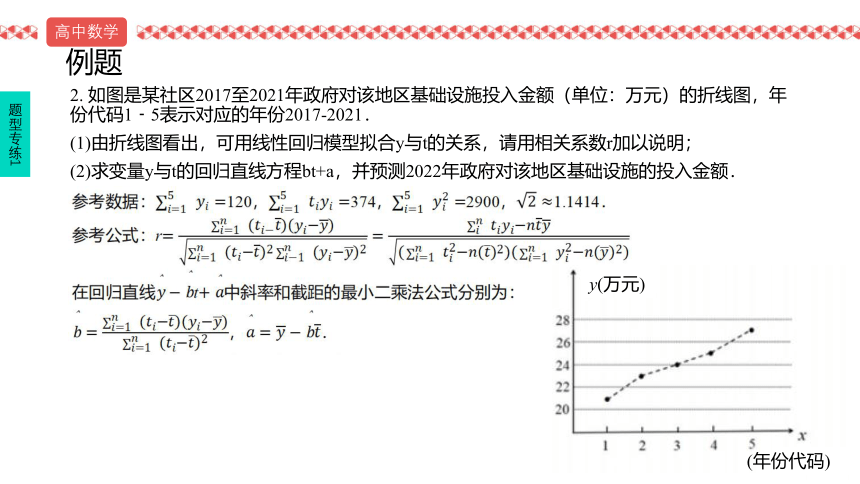
2. 如图是某社区2017至2021年政府对该地区基础设施投入金额(单位:万元)的折线图,年份代码1﹣5表示对应的年份2017-2021.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数r加以说明;
(2)求变量y与t的回归直线方程bt+a,并预测2022年政府对该地区基础设施的投入金额.
例题
y(万元)
(年份代码)
题型专练1
11
例题
题型专练1
利用回归直线方程可以进行预测与估计,但要注意回归直线方程表明的是两组数据之间的相关关系,而不是函数关系,所以利用该方程求出的数值都是估计值,而不是一个确定的数值.
求线性回归方程的一般步骤:
题型专练1
1.独立性检验:对于取值分别是{x1,x2}和{y1,y2}的分类变量X和Y,其样本频数列联表是:
则 (其中n=a+b+c+d为样本容量).
2.独立性检验的一般步骤
(1)根据样本数据列成2×2列联表;
(2)根据公式 ,计算K2的值;
(3)查表比较K2与临界值的大小关系,作统计判断.
3.K2的观测值k越大,对应假设事件H0成立(两类变量相互独立)的概率越小,H0不成立的概率越大.
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d n
题型专练2
14
例题
3.2021年春节,由贾玲导演的春节档电影《你好,李焕英》总票房已突破50亿元,影片的感人情节引起同学们广泛热议.开学后,某校团委在高三年级中(其中男生200名,女生150名),对是否观看该影片进行了问卷调查,各班男生观看人数统计记为A组,各班女生观看人数统计记为B组,得到如图的茎叶图.已知全年级恰有3个班级观看该影片的人数超过40.
(1)根据茎叶图绘制2×2列联表,并判断是否有97.5%的把握认为观看该影片与性别有关?
参考数据及公式如下:
P(K2≥k) 0.1 0.05 0.025 0.01 0.005 0.001
k 2.706 3.841 5.024 6.635 7.879 10.828
A组
B组
题型专练2
15
例题
题型专练2
16
例题
(2)若先从A组人数超过20的数据中随机抽取一个数据,再从B组人数少于20的数据中随机抽取一个数据,求抽到的这两个数据来自同一个班的概率.
参考数据及公式如下:
P(K2≥k) 0.1 0.05 0.025 0.01 0.005 0.001
k 2.706 3.841 5.024 6.635 7.879 10.828
题型专练2
17
例题
题型专练2
18
求解与独立性检验相交汇的问题
(1)读懂列联表:明确列联表中的数据.
(2)计算K2:根据提供的公式计算K2的值.
(3)作出判断:依据临界值与犯错误的概率得出结论.
(4)利用给定数据分析变量取值,计算概率.
题型专练2
19
练习
1.某社区管委会积极响应正在开展的“创文活动”,特制订了饲养宠物的管理规定.为了解社区住户对这个规定的态度(赞同与不赞同),工作人员随机调查了社区220户住户,将他们的态度和家里是否有宠物的情况进行了统计,得到如下2×2列联表(单位:户):
同时,工作人员还从上述调查的不赞同管理规定的住户中,用分层抽样的方法按家里有宠物、家里没有宠物抽取了6户组成样本T,进一步研究完善饲养宠物的管理规定.
(1)根据上述列联表,能否在犯错误的概率不超过0.001的前提下认为“社区住户对饲养宠物的管理规定的态度与家里是否有宠物有关系”?
赞同规定住户 不赞同规定住户 合计
家里有宠物住户 70 40 110
家里没有宠物住户 90 20 110
合计 160 60 220
题型专练2
20
练习
(2)工作人员在样本T中随机抽取2户住户进行访谈,求这2户住户中,至少有1户家里没有宠物的概率P(结果用数字表示).
题型专练2
21
练习
题型专练2
22
1.超几何分布:
在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则
2,…,m,其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*,此时称随机变量X服从超几
何分布.超几何分布的模型是不放回抽样,超几何分布中的参数是M,N,n.
2.离散型随机变量的均值、方差: (1)离散型随机变量ξ的分布列为:
离散型随机变量ξ的分布列具有两个性质:
①pi≥0; ②p1+p2+…+pi+…+pn=1(i=1,2,3,…,n).
ξ x1 x2 x3 … xi … n
P p1 p2 p3 … pi … pn
题型专练3
23
(2)E(ξ)=x1p1+x2p2+…+xipi+…+xnpn为随机变量ξ的数学期望或均值. D(ξ)=(x1-E(ξ))2·p1+(x2-E(ξ))2·p2+…+(xi-E(ξ))2·pi+…+(xn-E(ξ))2·pn叫做随机变量ξ的方差.
(3)数学期望、方差的性质. ①E(aξ+b)=aE(ξ)+b,D(aξ+b)=a2D(ξ). ②X~B(n,p),则E(X)=np,D(X)=np(1-p). ③X服从两点分布,则E(X)=p,D(X)=p(1-p).
题型专练3
24
例题——超几何分布
4.央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,它创新性地利用现代传媒手段实现了诗词娱乐化,用健康的娱乐化方式实现了“扩群”,体现了国人精神中对于优秀传统文化的呼唤与眷恋.在某市组织的诗词大赛中,某中学高中组与初中组成绩卓著.组委会进入该中学随机抽取了100名学生进行调查,将学生对诗词知识的掌握情况分为优秀、良好、一般三个等级,其中达到优秀等级的学生有70名.
(1)若该中学共有8000名学生,试估计该中学的学生中达到优秀等级的学生人数;
题型专练3
25
例题——超几何分布
(2)若抽取的达到优秀等级的70名学生中,高中生有40名,初中生有30名,利用分层抽样的方法从中抽取7名学生,然后从这7名学生中随机抽取3名学生代表该市参加比赛,记这3名学生中高中生的人数为X,求X的分布列与数学期望.
题型专练3
26
例题——超几何分布
题型专练3
27
【总结反思】
(1)超几何分布描述的是不放回抽样问题,随机变量为抽到的某类个体的个数.
(2)超几何分布的特征是:
①考察对象分两类; ②已知各类对象的个数;
③从中抽取若干个个体,考查某类个体个数X的概率分布.
(3)超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型.
题型专练3
28
独立重复试验与二项分布:
如果事件A在一次试验中发生的概率是p,那么它在n次独立重复试验中恰好发生k次的概率为
用X表示事件A在n次独立重复试验中发生的次数,
则X服从二项分布,即X~B(n,p)且
题型专练3
29
例题——二项分布
5.(漳州模拟)翡翠市场流行一种赌石“游戏规则”:翡翠在开采出来时有一层风化皮包裹着,无法知道其内的好坏,须切割后方能知道翡翠的价值,参加者先缴纳一定金额后可得到一块翡翠石并现场开石验证其具有的收藏价值.某举办商在赌石游戏中设置了甲、乙两种赌石规则,规则甲的赌中率为,赌中后可获得20万元;规则乙的赌中率为P0(0(1)收藏者张先生选择规则甲赌石,收藏者李先生选择规则乙赌石,记他们的累计获得金额数为X(单位:万元),若X≤30的概率为,求P0的大小;
题型专练3
30
例题——二项分布
题型专练3
31
例题——二项分布
(2)若收藏者张先生、李先生都选择赌石规则甲或选择赌石规则乙进行赌石,问:他们选择何种规则赌石,累计得到金额的数学期望最大?
题型专练3
32
例题——二项分布
题型专练3
33
【总结反思】
利用独立重复试验概率公式可以简化求概率的过程,但需要注意检验该概率模型是否满足公式
P(X=k)= pk(1-p)n-k的三个条件:
(1)在一次试验中某事件A发生的概率是一个常数p;
(2)n次试验不仅是在完全相同的情况下进行的重复试验,而且各次试验的结果是相互独立的;
(3)该公式表示n次试验中事件A恰好发生了k次的概率.
题型专练3
34
1.正态分布的定义
如果对于任何实数a,b(a<b),随机变量X满足P(a<X≤b)= ,则称随机变量X服从正
态分布,记为X~N(μ,σ2).其中
2.正态曲线的性质
①曲线位于x轴上方,与x轴不相交,与x轴之间的面积为1;
②曲线是单峰的,它关于直线x=μ对称;
③曲线在x=μ处达到峰值 ;
④当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,表示总体的分布越集中;
σ越大,曲线越“矮胖”,表示总体的分布越分散.
3.正态总体在三个特殊区间内取值的概率值
①P(μ-σ题型专练3
35
例题——正态分布
6.(潍坊模拟)为了严格监控某种零件的一条生产线的生产过程,某企业每天从该生产线上随机抽取10000个零件,并测量其内径(单位:cm.根据长期生产经验,认为这条生产线正常状态下生产的零件的内径X服从正态分布 .如果加工的零件内径小于 或大于
均为不合格品,其余为合格品.
(1)假设生产状态正常,请估计一天内抽取的10000个零件中不合格品的个数约为多少;
题型专练3
36
例题——正态分布
(2)若生产的某件产品为合格品则该件产品盈利;若生产的某件产品为不合格品则该件产品亏
损.已知每件产品的利润L(单位:元)与零件的内径X有如下关系:
求该企业一天从生产线上随机抽取10000个零件的平均利润.
题型专练3
37
例题——正态分布
题型专练3
38
概率与统计的综合问题
1.统计与概率的综合应用,意在考查考生的识图能力和数据处理能力.此类问题多涉及相互独
立事件、互斥事件的概率,在求解时,要明确基本事件的构成.
2.以统计图表为背景的随机变量分布列求解的关键:
(1)根据频率(数)分布表、频率分布直方图、茎叶图等图表准确求出随机事件的频率,并用之
估计相应概率;
(2)出现多个随机变量时,应注意分析随机变量之间的关系,进而由一个随机变量的分布列
推出另一个随机变量的分布列.
39
例题
7.2020年将全面建成小康社会,是党向人民作出的庄严承诺.目前脱贫攻坚已经进入冲刺阶段,某贫困县平原地区家庭与山区家庭的户数之比为3:2.用分层抽样的方法,收集了100户家庭2019年家庭年收入数据(单位:万元),绘制的频率直方图如图所示,样本中家庭年收入超过1.5万元的有10户居住在山区.
(1)完成2019年家庭年收入与地区的列联表,并判断是否有99.9%的把握认为该县2019年家庭年收入超过1.5万元与地区有关.
超过1.5万元 不超过1.5万元 总计
平原地区
山区 10
总计
P(K2≥k) 0.100 0.050 0.010 0.001
k 2.706 3.841 6.635 10.828
家庭收入
题型专练4
40
例题
解析:(1)由频率分布直方图可知,超过1.5万元的频率为(0.5+0.4+0.1)×0.5=0.5,
所以超过1.5万元的户数有100×0.5=50户,
又因为平原地区家庭与山区家庭的户数之比为3:2,抽取了100户,
故平原地区的共有60户,山区地区的共有40户,
又样本中家庭年收入超过1.5万元的有10户居住在山区,
所以超过1.5万元的有40户居住在平原地区,不超过1.5万元的有20户住在平原地区,
有30户住在山区地区,
故2019年家庭年收入与地区的列联表如下:
超过1.5万元 不超过1.5万元 总计
平原地区 40 20 60
山区 10 30 40
总计 50 50 100
所以有99.9%的把握认为该县2019年家庭年收入超过1.5万元与地区有关;
题型专练4
41
例题
(2)根据这100个样本数据,将频率视为概率.为了更好地落实党中央精准扶贫的决策,从2020年9月到12月,每月从该县2019年家庭年收入不超过1.5万元的家庭中选取4户作为“县长联系家庭”,记“县长联系家庭”是山区家庭的户数为X,求X的分布列和数学期望E(X).
家庭收入
题型专练4
42
例题
题型专练4
43
例题
8.从2020年元月份以来,全世界的经济都受到了新冠病毒的严重影响,我国抗疫战斗取得了重大的胜利,全国上下齐心协力复工复产,抓经济建设;某公司为了提升市场的占有率,准备对一项产品实施科技改造,经过充分的市场调研与模拟,得到x,y之间的五组数据如表:
其中,x(单位:百万元)是科技改造的总投入,y(单位:百万元)是改造后的额外收益;设U=2x+y是对当地生产总值增长的贡献值.
(1)若从五组数据中任取两组,求恰有一组满足U>30的概率;
x 2 3 5 7 8
y 5 8 12 14 16
题型专练4
44
例题
8.从2020年元月份以来,全世界的经济都受到了新冠病毒的严重影响,我国抗疫战斗取得了重大的胜利,全国上下齐心协力复工复产,抓经济建设;某公司为了提升市场的占有率,准备对一项产品实施科技改造,经过充分的市场调研与模拟,得到x,y之间的五组数据如表:
其中,x(单位:百万元)是科技改造的总投入,y(单位:百万元)是改造后的额外收益;设U=2x+y是对当地生产总值增长的贡献值.
(2)记 为U>20时的任意两组数据对应的贡献值的和,求随机变量 的分布列和数学期望;
x 2 3 5 7 8
y 5 8 12 14 16
题型专练4
45
例题
题型专练4
46
例题
(3)利用表中数据,甲、乙两个调研小组给出的拟合直线方程分别为甲组: ,乙组:
,试用最小二乘法判断哪条直线的拟合效果更好?
题型专练4
47
例题
题型专练4
相关系数:
(1)当r>0时,表明两个变量正相关;当r<0时,两个变量负相关.
(2)当|r|>0.75时,认为两个变量具有较强的线性相关关系.
求线性回归方程的一般步骤:
独立性检验的一般步骤
(1)根据样本数据列成2×2列联表;
(2)根据公式 ,计算K2的值;
(3)查表比较K2与临界值的大小关系,作统计判断.
当堂总结
1.独立重复试验与二项分布:
如果事件A在一次试验中发生的概率是p,那么它在n次独立重复试验中
恰好发生k次的概率为 用X
表示事件A在n次独立重复试验中发生的次数,
则X服从二项分布,即X~B(n,p)且
2.超几何分布:
在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则
2,…,m,其中m=min{M,n},且n≤N,
M≤N,n,M,N∈N*,此时称随机变量X服从超几何分布.超几何分布
的模型是不放回抽样,超几何分布中的参数是M,N,n.
当堂总结
求离散型随机变量的均值与方差的基本方法有:
(1)已知随机变量的分布列求它的均值、方差和标准差,可直接按定义(公式)求解;
(2)已知随机变量X的均值、方差,求X的线性函数Y=aX+b的均值、方差,可直接用均值、方差的性质求解,即E(aX+b)=aE(X)+b,D(aX+b)=a2D(X)
(a,b为常数);
(3)如能分析所给随机变量服从常用的分布,可直接利用它们的均值、方差公式求解,即若X服从两点分布,则E(X)=p,D(X)=p(1-p);若X~B(n,p),则E(X)=np,D(X)=np(1-p).
当堂总结
高考数学冲刺之解答题3
统计与概率
主讲人: |
2
01
解答题
三角函数与解三角形
02
解答题
立体几何
03
解答题
统计与概率
04
解答题
函数与导数
05
解答题
极坐标与参数方程
3
高考说明
近几年统计与概率问题主要以现实生活、古代文化为背景来考查统计图表的识别,排列与组合与古典概型的交汇,二项式定理,几何概型,双图(茎叶图、频率直方图)与离散型随机变量的分布列,统计案例相结合等,呈现考点模式化与考题应用化的特点,难度中等,题目为两小一大,分值在17到20分左右.
4
解答题的命题特点
(一)用定义法求解离散型随机变量的分布列,试题难度中等,综合考查排列组合知识和与互斥事件、对立事件以及相互独立事件的有关应用.
(二) 概型法求解随机变量的分布列的应用问题,试题难度中等,综合考查二项分布、正态分布、超几何分布等特殊分布和概率、统计知识的应用.
(三)公式法和比例法求解样本估计总体问题,试题难度中等,综合考查概率、抽样方法、统计图表、样本的数字特征的应用.
(四)模型法求解统计案例的问题,试题难度中等,综合考查概率统计与线性回归、独立性检验知识的应用.
(五)通过概率统计与函数、数列等知识的综合应用,综合考查概率统计在实际生活中的决策作用,试题难度较大.
5
本节说明
统计与概率:
类型一:变量间的相关关系 类型二:独立性检验
类型三:随机变量及其分布 类型四:统计与概率的综合
题型专练1
题型专练2
题型专练3
题型专练4
6
回归直线 经过样本点的中心 ,若x取某一个值代入回归直线方程
中,可求出y的估计值.
1.求回归直线方程的关键及实际应用:
(1)关键:正确理解 的计算公式和准确地计算.
(2)实际应用:在分析实际中两个变量的相关关系时,可根据样本数据作出散点图来确定两个
变量之间是否具有相关关系,若具有线性相关关系,则可通过线性回归方程估计和预测变
量的值.
2.相关系数:
(1)当r>0时,表明两个变量正相关;当r<0时,两个变量负相关.
(2)当|r|>0.75时,认为两个变量具有较强的线性相关关系.
题型专练1
7
例题
1. (安徽模拟)有一种速度叫中国速度,有一种骄傲叫中国高铁.中国高铁经过十几年的发展,取得了举世瞩目的成就,使我国完成了从较落后向先进铁路国的跨越式转变.中国的高铁技术不但越来越成熟,而且还走向国外,帮助不少国家修建了高铁.高铁可以说是中国一张行走的名片.截至到2020年,中国高铁运营里程已经达到3.9万公里.如表是2013年至2020年中国高铁每年的运营里程统计表,它反映了中国高铁近几年的飞速发展:
根据以上数据,回答下面问题.
(1)甲同学用曲线y=bx+a来拟合,并算得相关系数r1=0.97,乙同学用曲线y=cedx来拟合,并算得转化为线性回归方程所对应的相关系数r2=0.99,试问哪一个更适合作为y关于x的回归方程类型,并说明理由;
年份 2013 2014 2015 2016 2017 2018 2019 2020
年份代码x 1 2 3 4 5 6 7 8
运营里程y(万公里) 1.3 1.6 1.9 2.2 2.5 2.9 3.5 3.9
题型专练1
8
例题
(2)根据(1)的判断结果及表中数据,求y关于x的回归方程(系数精确到0.01).
参考公式:用最小二乘法求线性回归方程的系数公式:
题型专练1
9
例题
题型专练1
10
2. 如图是某社区2017至2021年政府对该地区基础设施投入金额(单位:万元)的折线图,年份代码1﹣5表示对应的年份2017-2021.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数r加以说明;
(2)求变量y与t的回归直线方程bt+a,并预测2022年政府对该地区基础设施的投入金额.
例题
y(万元)
(年份代码)
题型专练1
11
例题
题型专练1
利用回归直线方程可以进行预测与估计,但要注意回归直线方程表明的是两组数据之间的相关关系,而不是函数关系,所以利用该方程求出的数值都是估计值,而不是一个确定的数值.
求线性回归方程的一般步骤:
题型专练1
1.独立性检验:对于取值分别是{x1,x2}和{y1,y2}的分类变量X和Y,其样本频数列联表是:
则 (其中n=a+b+c+d为样本容量).
2.独立性检验的一般步骤
(1)根据样本数据列成2×2列联表;
(2)根据公式 ,计算K2的值;
(3)查表比较K2与临界值的大小关系,作统计判断.
3.K2的观测值k越大,对应假设事件H0成立(两类变量相互独立)的概率越小,H0不成立的概率越大.
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d n
题型专练2
14
例题
3.2021年春节,由贾玲导演的春节档电影《你好,李焕英》总票房已突破50亿元,影片的感人情节引起同学们广泛热议.开学后,某校团委在高三年级中(其中男生200名,女生150名),对是否观看该影片进行了问卷调查,各班男生观看人数统计记为A组,各班女生观看人数统计记为B组,得到如图的茎叶图.已知全年级恰有3个班级观看该影片的人数超过40.
(1)根据茎叶图绘制2×2列联表,并判断是否有97.5%的把握认为观看该影片与性别有关?
参考数据及公式如下:
P(K2≥k) 0.1 0.05 0.025 0.01 0.005 0.001
k 2.706 3.841 5.024 6.635 7.879 10.828
A组
B组
题型专练2
15
例题
题型专练2
16
例题
(2)若先从A组人数超过20的数据中随机抽取一个数据,再从B组人数少于20的数据中随机抽取一个数据,求抽到的这两个数据来自同一个班的概率.
参考数据及公式如下:
P(K2≥k) 0.1 0.05 0.025 0.01 0.005 0.001
k 2.706 3.841 5.024 6.635 7.879 10.828
题型专练2
17
例题
题型专练2
18
求解与独立性检验相交汇的问题
(1)读懂列联表:明确列联表中的数据.
(2)计算K2:根据提供的公式计算K2的值.
(3)作出判断:依据临界值与犯错误的概率得出结论.
(4)利用给定数据分析变量取值,计算概率.
题型专练2
19
练习
1.某社区管委会积极响应正在开展的“创文活动”,特制订了饲养宠物的管理规定.为了解社区住户对这个规定的态度(赞同与不赞同),工作人员随机调查了社区220户住户,将他们的态度和家里是否有宠物的情况进行了统计,得到如下2×2列联表(单位:户):
同时,工作人员还从上述调查的不赞同管理规定的住户中,用分层抽样的方法按家里有宠物、家里没有宠物抽取了6户组成样本T,进一步研究完善饲养宠物的管理规定.
(1)根据上述列联表,能否在犯错误的概率不超过0.001的前提下认为“社区住户对饲养宠物的管理规定的态度与家里是否有宠物有关系”?
赞同规定住户 不赞同规定住户 合计
家里有宠物住户 70 40 110
家里没有宠物住户 90 20 110
合计 160 60 220
题型专练2
20
练习
(2)工作人员在样本T中随机抽取2户住户进行访谈,求这2户住户中,至少有1户家里没有宠物的概率P(结果用数字表示).
题型专练2
21
练习
题型专练2
22
1.超几何分布:
在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则
2,…,m,其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*,此时称随机变量X服从超几
何分布.超几何分布的模型是不放回抽样,超几何分布中的参数是M,N,n.
2.离散型随机变量的均值、方差: (1)离散型随机变量ξ的分布列为:
离散型随机变量ξ的分布列具有两个性质:
①pi≥0; ②p1+p2+…+pi+…+pn=1(i=1,2,3,…,n).
ξ x1 x2 x3 … xi … n
P p1 p2 p3 … pi … pn
题型专练3
23
(2)E(ξ)=x1p1+x2p2+…+xipi+…+xnpn为随机变量ξ的数学期望或均值. D(ξ)=(x1-E(ξ))2·p1+(x2-E(ξ))2·p2+…+(xi-E(ξ))2·pi+…+(xn-E(ξ))2·pn叫做随机变量ξ的方差.
(3)数学期望、方差的性质. ①E(aξ+b)=aE(ξ)+b,D(aξ+b)=a2D(ξ). ②X~B(n,p),则E(X)=np,D(X)=np(1-p). ③X服从两点分布,则E(X)=p,D(X)=p(1-p).
题型专练3
24
例题——超几何分布
4.央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,它创新性地利用现代传媒手段实现了诗词娱乐化,用健康的娱乐化方式实现了“扩群”,体现了国人精神中对于优秀传统文化的呼唤与眷恋.在某市组织的诗词大赛中,某中学高中组与初中组成绩卓著.组委会进入该中学随机抽取了100名学生进行调查,将学生对诗词知识的掌握情况分为优秀、良好、一般三个等级,其中达到优秀等级的学生有70名.
(1)若该中学共有8000名学生,试估计该中学的学生中达到优秀等级的学生人数;
题型专练3
25
例题——超几何分布
(2)若抽取的达到优秀等级的70名学生中,高中生有40名,初中生有30名,利用分层抽样的方法从中抽取7名学生,然后从这7名学生中随机抽取3名学生代表该市参加比赛,记这3名学生中高中生的人数为X,求X的分布列与数学期望.
题型专练3
26
例题——超几何分布
题型专练3
27
【总结反思】
(1)超几何分布描述的是不放回抽样问题,随机变量为抽到的某类个体的个数.
(2)超几何分布的特征是:
①考察对象分两类; ②已知各类对象的个数;
③从中抽取若干个个体,考查某类个体个数X的概率分布.
(3)超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型.
题型专练3
28
独立重复试验与二项分布:
如果事件A在一次试验中发生的概率是p,那么它在n次独立重复试验中恰好发生k次的概率为
用X表示事件A在n次独立重复试验中发生的次数,
则X服从二项分布,即X~B(n,p)且
题型专练3
29
例题——二项分布
5.(漳州模拟)翡翠市场流行一种赌石“游戏规则”:翡翠在开采出来时有一层风化皮包裹着,无法知道其内的好坏,须切割后方能知道翡翠的价值,参加者先缴纳一定金额后可得到一块翡翠石并现场开石验证其具有的收藏价值.某举办商在赌石游戏中设置了甲、乙两种赌石规则,规则甲的赌中率为,赌中后可获得20万元;规则乙的赌中率为P0(0
题型专练3
30
例题——二项分布
题型专练3
31
例题——二项分布
(2)若收藏者张先生、李先生都选择赌石规则甲或选择赌石规则乙进行赌石,问:他们选择何种规则赌石,累计得到金额的数学期望最大?
题型专练3
32
例题——二项分布
题型专练3
33
【总结反思】
利用独立重复试验概率公式可以简化求概率的过程,但需要注意检验该概率模型是否满足公式
P(X=k)= pk(1-p)n-k的三个条件:
(1)在一次试验中某事件A发生的概率是一个常数p;
(2)n次试验不仅是在完全相同的情况下进行的重复试验,而且各次试验的结果是相互独立的;
(3)该公式表示n次试验中事件A恰好发生了k次的概率.
题型专练3
34
1.正态分布的定义
如果对于任何实数a,b(a<b),随机变量X满足P(a<X≤b)= ,则称随机变量X服从正
态分布,记为X~N(μ,σ2).其中
2.正态曲线的性质
①曲线位于x轴上方,与x轴不相交,与x轴之间的面积为1;
②曲线是单峰的,它关于直线x=μ对称;
③曲线在x=μ处达到峰值 ;
④当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,表示总体的分布越集中;
σ越大,曲线越“矮胖”,表示总体的分布越分散.
3.正态总体在三个特殊区间内取值的概率值
①P(μ-σ
35
例题——正态分布
6.(潍坊模拟)为了严格监控某种零件的一条生产线的生产过程,某企业每天从该生产线上随机抽取10000个零件,并测量其内径(单位:cm.根据长期生产经验,认为这条生产线正常状态下生产的零件的内径X服从正态分布 .如果加工的零件内径小于 或大于
均为不合格品,其余为合格品.
(1)假设生产状态正常,请估计一天内抽取的10000个零件中不合格品的个数约为多少;
题型专练3
36
例题——正态分布
(2)若生产的某件产品为合格品则该件产品盈利;若生产的某件产品为不合格品则该件产品亏
损.已知每件产品的利润L(单位:元)与零件的内径X有如下关系:
求该企业一天从生产线上随机抽取10000个零件的平均利润.
题型专练3
37
例题——正态分布
题型专练3
38
概率与统计的综合问题
1.统计与概率的综合应用,意在考查考生的识图能力和数据处理能力.此类问题多涉及相互独
立事件、互斥事件的概率,在求解时,要明确基本事件的构成.
2.以统计图表为背景的随机变量分布列求解的关键:
(1)根据频率(数)分布表、频率分布直方图、茎叶图等图表准确求出随机事件的频率,并用之
估计相应概率;
(2)出现多个随机变量时,应注意分析随机变量之间的关系,进而由一个随机变量的分布列
推出另一个随机变量的分布列.
39
例题
7.2020年将全面建成小康社会,是党向人民作出的庄严承诺.目前脱贫攻坚已经进入冲刺阶段,某贫困县平原地区家庭与山区家庭的户数之比为3:2.用分层抽样的方法,收集了100户家庭2019年家庭年收入数据(单位:万元),绘制的频率直方图如图所示,样本中家庭年收入超过1.5万元的有10户居住在山区.
(1)完成2019年家庭年收入与地区的列联表,并判断是否有99.9%的把握认为该县2019年家庭年收入超过1.5万元与地区有关.
超过1.5万元 不超过1.5万元 总计
平原地区
山区 10
总计
P(K2≥k) 0.100 0.050 0.010 0.001
k 2.706 3.841 6.635 10.828
家庭收入
题型专练4
40
例题
解析:(1)由频率分布直方图可知,超过1.5万元的频率为(0.5+0.4+0.1)×0.5=0.5,
所以超过1.5万元的户数有100×0.5=50户,
又因为平原地区家庭与山区家庭的户数之比为3:2,抽取了100户,
故平原地区的共有60户,山区地区的共有40户,
又样本中家庭年收入超过1.5万元的有10户居住在山区,
所以超过1.5万元的有40户居住在平原地区,不超过1.5万元的有20户住在平原地区,
有30户住在山区地区,
故2019年家庭年收入与地区的列联表如下:
超过1.5万元 不超过1.5万元 总计
平原地区 40 20 60
山区 10 30 40
总计 50 50 100
所以有99.9%的把握认为该县2019年家庭年收入超过1.5万元与地区有关;
题型专练4
41
例题
(2)根据这100个样本数据,将频率视为概率.为了更好地落实党中央精准扶贫的决策,从2020年9月到12月,每月从该县2019年家庭年收入不超过1.5万元的家庭中选取4户作为“县长联系家庭”,记“县长联系家庭”是山区家庭的户数为X,求X的分布列和数学期望E(X).
家庭收入
题型专练4
42
例题
题型专练4
43
例题
8.从2020年元月份以来,全世界的经济都受到了新冠病毒的严重影响,我国抗疫战斗取得了重大的胜利,全国上下齐心协力复工复产,抓经济建设;某公司为了提升市场的占有率,准备对一项产品实施科技改造,经过充分的市场调研与模拟,得到x,y之间的五组数据如表:
其中,x(单位:百万元)是科技改造的总投入,y(单位:百万元)是改造后的额外收益;设U=2x+y是对当地生产总值增长的贡献值.
(1)若从五组数据中任取两组,求恰有一组满足U>30的概率;
x 2 3 5 7 8
y 5 8 12 14 16
题型专练4
44
例题
8.从2020年元月份以来,全世界的经济都受到了新冠病毒的严重影响,我国抗疫战斗取得了重大的胜利,全国上下齐心协力复工复产,抓经济建设;某公司为了提升市场的占有率,准备对一项产品实施科技改造,经过充分的市场调研与模拟,得到x,y之间的五组数据如表:
其中,x(单位:百万元)是科技改造的总投入,y(单位:百万元)是改造后的额外收益;设U=2x+y是对当地生产总值增长的贡献值.
(2)记 为U>20时的任意两组数据对应的贡献值的和,求随机变量 的分布列和数学期望;
x 2 3 5 7 8
y 5 8 12 14 16
题型专练4
45
例题
题型专练4
46
例题
(3)利用表中数据,甲、乙两个调研小组给出的拟合直线方程分别为甲组: ,乙组:
,试用最小二乘法判断哪条直线的拟合效果更好?
题型专练4
47
例题
题型专练4
相关系数:
(1)当r>0时,表明两个变量正相关;当r<0时,两个变量负相关.
(2)当|r|>0.75时,认为两个变量具有较强的线性相关关系.
求线性回归方程的一般步骤:
独立性检验的一般步骤
(1)根据样本数据列成2×2列联表;
(2)根据公式 ,计算K2的值;
(3)查表比较K2与临界值的大小关系,作统计判断.
当堂总结
1.独立重复试验与二项分布:
如果事件A在一次试验中发生的概率是p,那么它在n次独立重复试验中
恰好发生k次的概率为 用X
表示事件A在n次独立重复试验中发生的次数,
则X服从二项分布,即X~B(n,p)且
2.超几何分布:
在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则
2,…,m,其中m=min{M,n},且n≤N,
M≤N,n,M,N∈N*,此时称随机变量X服从超几何分布.超几何分布
的模型是不放回抽样,超几何分布中的参数是M,N,n.
当堂总结
求离散型随机变量的均值与方差的基本方法有:
(1)已知随机变量的分布列求它的均值、方差和标准差,可直接按定义(公式)求解;
(2)已知随机变量X的均值、方差,求X的线性函数Y=aX+b的均值、方差,可直接用均值、方差的性质求解,即E(aX+b)=aE(X)+b,D(aX+b)=a2D(X)
(a,b为常数);
(3)如能分析所给随机变量服从常用的分布,可直接利用它们的均值、方差公式求解,即若X服从两点分布,则E(X)=p,D(X)=p(1-p);若X~B(n,p),则E(X)=np,D(X)=np(1-p).
当堂总结
同课章节目录
