《微积分基本定理》参考课件
图片预览




文档简介
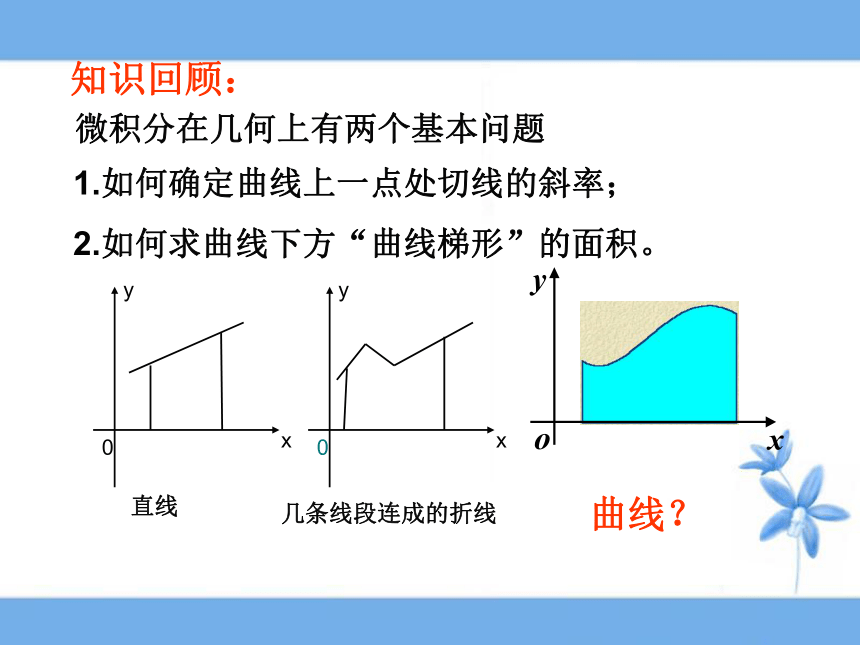
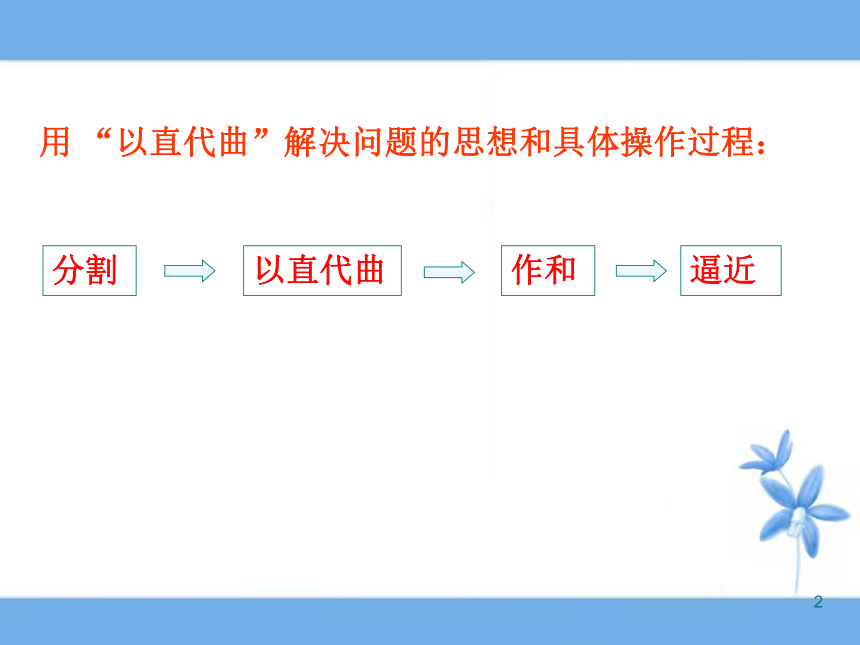
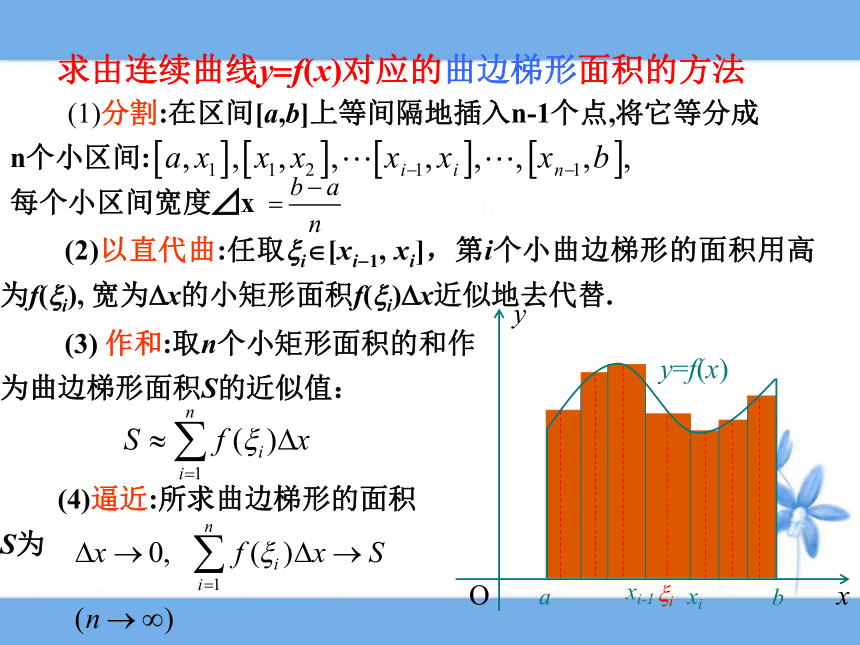
课件19张PPT。微积分在几何上有两个基本问题1.如何确定曲线上一点处切线的斜率;2.如何求曲线下方“曲线梯形”的面积。直线几条线段连成的折线曲线?知识回顾:2用 “以直代曲”解决问题的思想和具体操作过程:分割以直代曲作和逼近求由连续曲线y=f(x)对应的曲边梯形面积的方法 (2)以直代曲:任取xi?[xi-1, xi],第i个小曲边梯形的面积用高为f(xi), 宽为Dx的小矩形面积f(xi)Dx近似地去代替. (4)逼近:所求曲边梯形的面积S为 (3) 作和:取n个小矩形面积的和作为曲边梯形面积S的近似值:xi-1xixi (1)分割:在区间[a,b]上等间隔地插入n-1个点,将它等分成
n个小区间:
每个小区间宽度⊿x定积分的定义:一般地,设函数f(x)在区间[a,b]上有定义,将区间[a,b]等分成n个小区间,每个小区的长度为 ,在每个小区间上取一点,依次为x1,x2,…….xi,….xn,作和
如果 无限趋近于0时,Sn无限趋近于常数S,那么称常数S为函数f(x)在区间[a,b]上的定积分,记作: . 由定积分的定义可以计算 , 但比较麻烦(四步曲),有没有更加简便有效的方法求定积分呢?问题情景(分割---以直代曲----求和------逼近)微积分基本定理变速直线运动中位置函数与速度函数的联系变速直线运动中路程为这段路程可表示为问题思考另一方面作变速直线运动的物体的运动规律是s=s(t), 对于一般函数,设是否也有 若上式成立,的原函数来计算我们就找到了用定理 (微积分基本定理)牛顿—莱布尼茨公式记:则:f(x)是F(x)的导函数F(x) 是f(x)的原函数解:(1)取解:(2)取例 计算下列定积分 解:(3)∵例 计算下列定积分 2019/1/25解(1)∵例 计算下列定积分 例 .计算下列定积分 解(1)∵01解00解 练习: 29/619e2-e+1 练习: 微积分基本公式小结牛顿-莱布尼茨公式沟通了导数与定积分之间的关系.
n个小区间:
每个小区间宽度⊿x定积分的定义:一般地,设函数f(x)在区间[a,b]上有定义,将区间[a,b]等分成n个小区间,每个小区的长度为 ,在每个小区间上取一点,依次为x1,x2,…….xi,….xn,作和
如果 无限趋近于0时,Sn无限趋近于常数S,那么称常数S为函数f(x)在区间[a,b]上的定积分,记作: . 由定积分的定义可以计算 , 但比较麻烦(四步曲),有没有更加简便有效的方法求定积分呢?问题情景(分割---以直代曲----求和------逼近)微积分基本定理变速直线运动中位置函数与速度函数的联系变速直线运动中路程为这段路程可表示为问题思考另一方面作变速直线运动的物体的运动规律是s=s(t), 对于一般函数,设是否也有 若上式成立,的原函数来计算我们就找到了用定理 (微积分基本定理)牛顿—莱布尼茨公式记:则:f(x)是F(x)的导函数F(x) 是f(x)的原函数解:(1)取解:(2)取例 计算下列定积分 解:(3)∵例 计算下列定积分 2019/1/25解(1)∵例 计算下列定积分 例 .计算下列定积分 解(1)∵01解00解 练习: 29/619e2-e+1 练习: 微积分基本公式小结牛顿-莱布尼茨公式沟通了导数与定积分之间的关系.
