苏科版 九年级下册 9.3概率及其应用 课件(共34张PPT)
文档属性
| 名称 | 苏科版 九年级下册 9.3概率及其应用 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 22:46:51 | ||
图片预览









文档简介
(共34张PPT)
概率及其应用
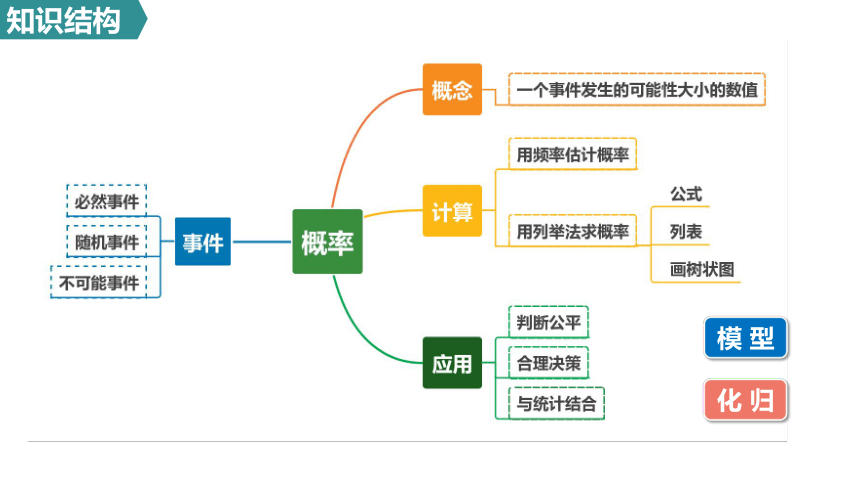
知识结构
模 型
化 归
热身训练
【热身训练1】
下列事件是必然事件的是( )
A.没有水分,种子发芽
B.如果a,b都是实数,那么a+b=b+a
C.打开电视,正在播广告
D.抛掷一枚质地均匀的硬币,正面向上
热身训练
【热身训练2】
社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象如图所示,试估计“摸出黑球”的概率为_______.
热身训练
【热身训练3】
在一个不透明的袋中装有5个球,其中2个红球,3个白球,这些球除颜色外无其他差别,从中随机摸出1个球,摸出红球的概率是( )
A. B. C. D.
热身训练
【热身训练3】变式:
在一个不透明的袋中装有2个红球还有一些白球,这些球除颜色外无其他差别,从中随机摸出1个球,摸出红球的概率是 ,则白球的个数是_______个.
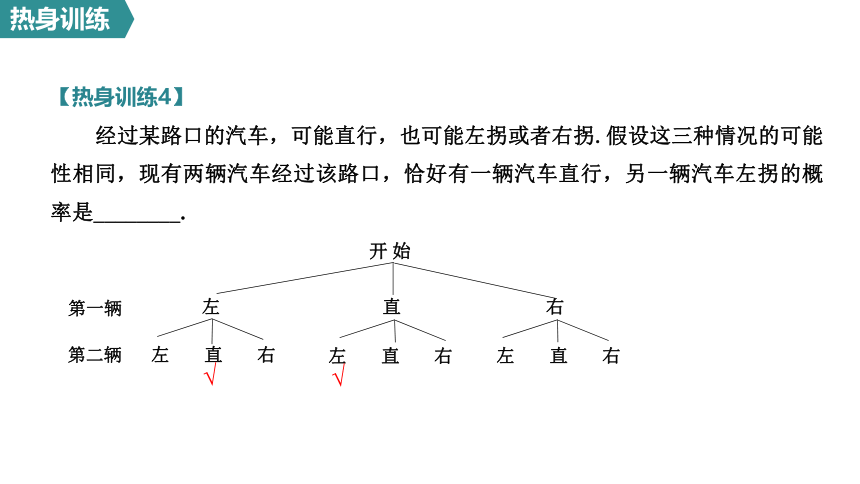
【热身训练4】
经过某路口的汽车,可能直行,也可能左拐或者右拐.假设这三种情况的可能性相同,现有两辆汽车经过该路口,恰好有一辆汽车直行,另一辆汽车左拐的概率是________.
热身训练
第一辆
第二辆
左 直 右
开 始
左 直 右
左 直 右
左 直 右
√
√
热身训练
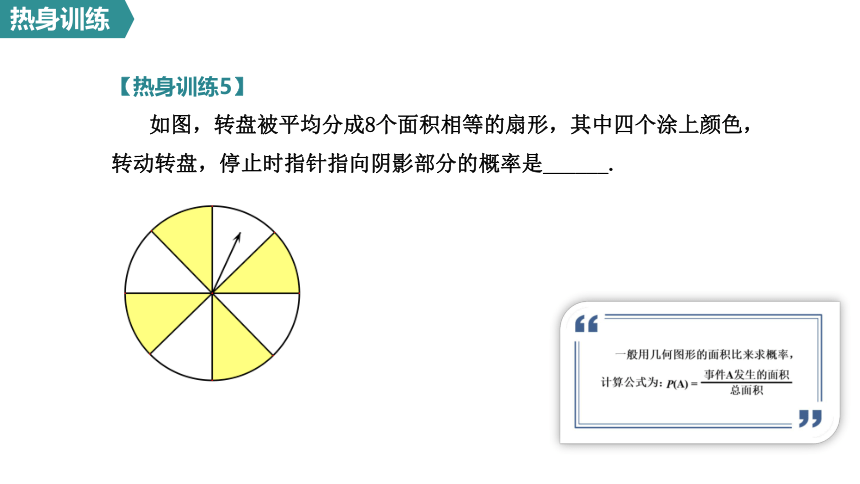
【热身训练5】
如图,转盘被平均分成8个面积相等的扇形,其中四个涂上颜色,转动转盘,停止时指针指向阴影部分的概率是______.
判断事件
概率
概率的计算
概率的应用
考点梳理
用频率估计概率
列举法求概率
用面积求概率
典型例题
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中. 有下列事件:
从中随机抽出1支签,标号为5;
从中随机抽出1支签,标号小于6;
从中随机抽出1支签,标号为奇数;
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
(1)______是必然事件,______是不可能事件,_______是随机事件;
判断事件
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中. 有下列事件:
从中随机抽出1支签,标号为5;
从中随机抽出1支签,标号小于6;
从中随机抽出1支签,标号为奇数;
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
(2)事件______发生的可能性最大,事件______发生的可能性最小;
比较可能性的大小
典型例题
(3)事件③发生的概率是______;
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中. 有下列事件:
从中随机抽出1支签,标号为5;
从中随机抽出1支签,标号小于6;
从中随机抽出1支签,标号为奇数;
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
一步概率
典型例题
热身训练
(4)求事件 发生的概率.
典型例题
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中. 有下列事件:
从中随机抽出1支签,标号为5;
从中随机抽出1支签,标号小于6;
从中随机抽出1支签,标号为奇数;
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
两步概率
放回
开 始
1 2 3 4
√
√
√
√
第1支
第2支
由图可知,共有16种等可能的结果,其中两次标号相同的有4种, ∴
典型例题
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
(4)求事件 发生的概率.
解:画树状图如图:
1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
一支
二支
结果
√
√
√
√
典型例题
由表可知,共有16种等可能的结果,其中两次标号相同的有4种,∴
(4)求事件 发生的概率.
解:列表如下:
列举法类别 适用条件 具体步骤方法
公式 事件涉及的对象较单一且出现的等可能结果数目较少 用公式P(A)= 计算概率
列表 一次试验涉及两个因素并且出现的等可能结果数目较多 1.选一次操作(或一个条件)为横行,另一次操作(或另一个条件)为竖列,列出表格;
2.用公式P( A )= 计算概率
画树状图 当一次试验涉及两个或更多个因素
1.画树状图;
2 .运用公式P(A)= 计算概率
一步概率
两步概率
两步概率
三步概率
列举法求概率
变式1:随机抽出1支签后不放回,再随机抽出1支签,求抽出的两支签标号都是奇数的概率.
典型例题
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中.
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
两步概率
不放回
第1支
第2支
1 2 3 4
开 始
2 3 4
1 2 3
1 3 4
1 2 4
√
√
由图可知,共有12种等可能的结果,其中都是奇数的有2种
解:画树状图如下:
1 2 3 4
1 (2,1) (3,1) (4,1)
2 (1,2) (3,2) (4,2)
3 (1,3) (2,3) (4,3)
4 (1,4) (2,4) (3,4)
一支
二支
结果
√
√
典型例题
两步概率
不放回
由表可知,共有12种等可能的结果,其中都是奇数的有2种, ∴
解:列表如下:
变式2:随机同时抽取两支签,求两次抽出的签标号的和等于5的概率.
典型例题
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中.
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
两步概率
不放回
第1支
第2支
1 2 3 4
和 3 4 5 3 5 6 4 5 7 5 6 7
开 始
2 3 4
1 2 3
1 3 4
1 2 4
由图可知,共有12种等可能的结果,其中和为5的有4种, ∴
√
√
√
√
解:画树状图如下:
1 2 3 4
1 3 4 5
2 3 5 6
3 4 5 7
4 5 6 7
一支
二支
结果
√
√
√
√
典型例题
两步概率
不放回
由表可知,共有12种等可能的结果,其中和为5的有4种, ∴
解:列表如下:
典型例题
在甲乙两个不透明的盒子中分别有四张完全相同的小纸条做成4支签,甲盒中的四支签分别标上1、2、3、4这四个号码,乙盒中的四支签分别标上5、6、7、8这四个号码.
从两个盒子中分别随机抽出1支签,求甲、乙两盒中抽出的签之和能被3整除的概率.
变式3:
甲
乙
开 始
1 2 3 4
5 6 7 8
5 6 7 8
5 6 7 8
5 6 7 8
和 6 7 8 9 7 8 9 10 8 9 10 11 9 10 11 12
√
√
√
√
√
√
由图可知,共有16种等可能的结果,其中符合要求的有6种, ∴
两步概率
放回
解:画树状图如下:
典型例题
在甲乙两个不透明的盒子中分别有四张完全相同的小纸条做成4支签,甲盒中的四支签分别标上1、2、3、4这四个号码,乙盒中的四支签分别标上5、6、7、8这四个号码.
从两个盒子中分别随机抽出1支签,求甲、乙两盒中抽出的签之和能被3整除的概率.
变式3:
由表可知,共有16种等可能的结果,其中符合要求的有6种,∴
1 2 3 4
5 6 7 8 9
6 7 8 9 10
7 8 9 10 11
8 9 10 11 12
√
√
√
√
√
√
甲
乙
和
解:列表如下:
两步概率
放回
方法梳理
转化
为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:
请根据统计表中提供的信息解答下列问题:
(1)填空:a= ,b= ,c= .
(2)这些家庭中月平均用水量数据的平均数是 ,众数是 ,中位数是 .
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
应用概率
与统计结合
【解答】解:(1)抽查的户数为:4÷0.08=50(户),
∴a=50×0.40=20,b=9÷50=0.18,c=10÷50=0.2,
故答案为:20,0.18,0.2;
(2)这些家庭中月平均用水量数据的平均数 (吨),
众数是4吨,中位数为 (吨),
故答案为:4.92,4,5;
(3)∵4+20+9=33(户),
∴估计该市直属机关200户家庭中月平均用水量不超过5吨的约有: (户);
应用概率
由图可知,共有12种等可能的结果,恰好选到甲、丙两户的结果有2种,
∴恰好选到甲、丙两户的概率为 ,
所有等可能的结果分别为(甲,乙)、(甲,丙)、(甲,丁)、(乙,甲)、(乙,丙)、(乙,丁)、(丙,甲)、(丙,乙)、(丁,甲)、(丁,乙)、(丁,丙)、(甲,丙).
第1户
第2户
开 始
甲 乙 丙 丁
乙 丙 丁 甲 丙 丁 甲 乙 丁 甲 乙 丙
√
√
(4)画树状图如下:
应用概率
应用概率
4张相同的卡片上分别写有数字0,1,-2,3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是负数的概率为________;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?
(请用树状图或列表等方法说明理由)
判断公平
0 -1 2 3
0 -1 2 3
-1 1 3 4
2 -2 -3 1
3 -3 -4 -1
差
一
二
2.已知电流在一定时间段内正常通过电子元件“ ”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
A.0.75 B.0.525 C.0.5 D.0.25
应用概率
1.在单词mathematics(数学)中任意选择一个字母恰好是字母“t”的概率是 _____.
跨学科融合
3. 五张不透明的卡片,正面分别写有实数 5.060060006…(相邻两个6之间0的个数依次加1),这五张卡片除正面的数不同外其余都相同,将它们背面朝上混合均匀后任取一张卡片,取到的卡片正面的数是无理数的概率是________.
应用概率
4. 从背面朝上的分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,随机抽取一张,则所抽得的图形既是中心对称图形又是轴对称图形的概率为_______.
学科内知识点融合
无理数
轴对称、中心对称图形
5.小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中
只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个
图案中有3个正方体,第(3)个图案中有6个正方体,…按照此规律,从第(100)个图案所需正方体中
随机抽取一个正方体,抽到带“心”字正方体的概率是________.
应用概率
找规律
6. 圆周率π是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前,超级计算机已计算出的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从π的小数部分随机取出一个数字,估计数字是6的概率为________;
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)
应用概率
数学史
7. 我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和如图1,ar+cq+bp是该三角形的顺序旋转和,ap+bq+cr是该三角形的逆序旋转和.已知某三角形的特征值如图2,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数z,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是_________.
应用概率
新定义
判断事件
概率
概率的计算
概率的应用
小结
用频率估计概率
列举法求概率
用面积求概率
一步概率
两步概率
三步概率
同学们,再见!
概率及其应用
知识结构
模 型
化 归
热身训练
【热身训练1】
下列事件是必然事件的是( )
A.没有水分,种子发芽
B.如果a,b都是实数,那么a+b=b+a
C.打开电视,正在播广告
D.抛掷一枚质地均匀的硬币,正面向上
热身训练
【热身训练2】
社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象如图所示,试估计“摸出黑球”的概率为_______.
热身训练
【热身训练3】
在一个不透明的袋中装有5个球,其中2个红球,3个白球,这些球除颜色外无其他差别,从中随机摸出1个球,摸出红球的概率是( )
A. B. C. D.
热身训练
【热身训练3】变式:
在一个不透明的袋中装有2个红球还有一些白球,这些球除颜色外无其他差别,从中随机摸出1个球,摸出红球的概率是 ,则白球的个数是_______个.
【热身训练4】
经过某路口的汽车,可能直行,也可能左拐或者右拐.假设这三种情况的可能性相同,现有两辆汽车经过该路口,恰好有一辆汽车直行,另一辆汽车左拐的概率是________.
热身训练
第一辆
第二辆
左 直 右
开 始
左 直 右
左 直 右
左 直 右
√
√
热身训练
【热身训练5】
如图,转盘被平均分成8个面积相等的扇形,其中四个涂上颜色,转动转盘,停止时指针指向阴影部分的概率是______.
判断事件
概率
概率的计算
概率的应用
考点梳理
用频率估计概率
列举法求概率
用面积求概率
典型例题
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中. 有下列事件:
从中随机抽出1支签,标号为5;
从中随机抽出1支签,标号小于6;
从中随机抽出1支签,标号为奇数;
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
(1)______是必然事件,______是不可能事件,_______是随机事件;
判断事件
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中. 有下列事件:
从中随机抽出1支签,标号为5;
从中随机抽出1支签,标号小于6;
从中随机抽出1支签,标号为奇数;
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
(2)事件______发生的可能性最大,事件______发生的可能性最小;
比较可能性的大小
典型例题
(3)事件③发生的概率是______;
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中. 有下列事件:
从中随机抽出1支签,标号为5;
从中随机抽出1支签,标号小于6;
从中随机抽出1支签,标号为奇数;
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
一步概率
典型例题
热身训练
(4)求事件 发生的概率.
典型例题
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中. 有下列事件:
从中随机抽出1支签,标号为5;
从中随机抽出1支签,标号小于6;
从中随机抽出1支签,标号为奇数;
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
两步概率
放回
开 始
1 2 3 4
√
√
√
√
第1支
第2支
由图可知,共有16种等可能的结果,其中两次标号相同的有4种, ∴
典型例题
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
(4)求事件 发生的概率.
解:画树状图如图:
1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
一支
二支
结果
√
√
√
√
典型例题
由表可知,共有16种等可能的结果,其中两次标号相同的有4种,∴
(4)求事件 发生的概率.
解:列表如下:
列举法类别 适用条件 具体步骤方法
公式 事件涉及的对象较单一且出现的等可能结果数目较少 用公式P(A)= 计算概率
列表 一次试验涉及两个因素并且出现的等可能结果数目较多 1.选一次操作(或一个条件)为横行,另一次操作(或另一个条件)为竖列,列出表格;
2.用公式P( A )= 计算概率
画树状图 当一次试验涉及两个或更多个因素
1.画树状图;
2 .运用公式P(A)= 计算概率
一步概率
两步概率
两步概率
三步概率
列举法求概率
变式1:随机抽出1支签后不放回,再随机抽出1支签,求抽出的两支签标号都是奇数的概率.
典型例题
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中.
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
两步概率
不放回
第1支
第2支
1 2 3 4
开 始
2 3 4
1 2 3
1 3 4
1 2 4
√
√
由图可知,共有12种等可能的结果,其中都是奇数的有2种
解:画树状图如下:
1 2 3 4
1 (2,1) (3,1) (4,1)
2 (1,2) (3,2) (4,2)
3 (1,3) (2,3) (4,3)
4 (1,4) (2,4) (3,4)
一支
二支
结果
√
√
典型例题
两步概率
不放回
由表可知,共有12种等可能的结果,其中都是奇数的有2种, ∴
解:列表如下:
变式2:随机同时抽取两支签,求两次抽出的签标号的和等于5的概率.
典型例题
在四张完全相同的小纸条上分别标上1、2、3、4这四个号码,做成4支签,放在一个不透明的盒子中.
从中随机抽出1支签,放回后再抽出1支签,两支签标号相同.
两步概率
不放回
第1支
第2支
1 2 3 4
和 3 4 5 3 5 6 4 5 7 5 6 7
开 始
2 3 4
1 2 3
1 3 4
1 2 4
由图可知,共有12种等可能的结果,其中和为5的有4种, ∴
√
√
√
√
解:画树状图如下:
1 2 3 4
1 3 4 5
2 3 5 6
3 4 5 7
4 5 6 7
一支
二支
结果
√
√
√
√
典型例题
两步概率
不放回
由表可知,共有12种等可能的结果,其中和为5的有4种, ∴
解:列表如下:
典型例题
在甲乙两个不透明的盒子中分别有四张完全相同的小纸条做成4支签,甲盒中的四支签分别标上1、2、3、4这四个号码,乙盒中的四支签分别标上5、6、7、8这四个号码.
从两个盒子中分别随机抽出1支签,求甲、乙两盒中抽出的签之和能被3整除的概率.
变式3:
甲
乙
开 始
1 2 3 4
5 6 7 8
5 6 7 8
5 6 7 8
5 6 7 8
和 6 7 8 9 7 8 9 10 8 9 10 11 9 10 11 12
√
√
√
√
√
√
由图可知,共有16种等可能的结果,其中符合要求的有6种, ∴
两步概率
放回
解:画树状图如下:
典型例题
在甲乙两个不透明的盒子中分别有四张完全相同的小纸条做成4支签,甲盒中的四支签分别标上1、2、3、4这四个号码,乙盒中的四支签分别标上5、6、7、8这四个号码.
从两个盒子中分别随机抽出1支签,求甲、乙两盒中抽出的签之和能被3整除的概率.
变式3:
由表可知,共有16种等可能的结果,其中符合要求的有6种,∴
1 2 3 4
5 6 7 8 9
6 7 8 9 10
7 8 9 10 11
8 9 10 11 12
√
√
√
√
√
√
甲
乙
和
解:列表如下:
两步概率
放回
方法梳理
转化
为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:
请根据统计表中提供的信息解答下列问题:
(1)填空:a= ,b= ,c= .
(2)这些家庭中月平均用水量数据的平均数是 ,众数是 ,中位数是 .
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
应用概率
与统计结合
【解答】解:(1)抽查的户数为:4÷0.08=50(户),
∴a=50×0.40=20,b=9÷50=0.18,c=10÷50=0.2,
故答案为:20,0.18,0.2;
(2)这些家庭中月平均用水量数据的平均数 (吨),
众数是4吨,中位数为 (吨),
故答案为:4.92,4,5;
(3)∵4+20+9=33(户),
∴估计该市直属机关200户家庭中月平均用水量不超过5吨的约有: (户);
应用概率
由图可知,共有12种等可能的结果,恰好选到甲、丙两户的结果有2种,
∴恰好选到甲、丙两户的概率为 ,
所有等可能的结果分别为(甲,乙)、(甲,丙)、(甲,丁)、(乙,甲)、(乙,丙)、(乙,丁)、(丙,甲)、(丙,乙)、(丁,甲)、(丁,乙)、(丁,丙)、(甲,丙).
第1户
第2户
开 始
甲 乙 丙 丁
乙 丙 丁 甲 丙 丁 甲 乙 丁 甲 乙 丙
√
√
(4)画树状图如下:
应用概率
应用概率
4张相同的卡片上分别写有数字0,1,-2,3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是负数的概率为________;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?
(请用树状图或列表等方法说明理由)
判断公平
0 -1 2 3
0 -1 2 3
-1 1 3 4
2 -2 -3 1
3 -3 -4 -1
差
一
二
2.已知电流在一定时间段内正常通过电子元件“ ”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
A.0.75 B.0.525 C.0.5 D.0.25
应用概率
1.在单词mathematics(数学)中任意选择一个字母恰好是字母“t”的概率是 _____.
跨学科融合
3. 五张不透明的卡片,正面分别写有实数 5.060060006…(相邻两个6之间0的个数依次加1),这五张卡片除正面的数不同外其余都相同,将它们背面朝上混合均匀后任取一张卡片,取到的卡片正面的数是无理数的概率是________.
应用概率
4. 从背面朝上的分别画有等腰三角形、平行四边形、矩形、圆的四张形状、大小相同的卡片中,随机抽取一张,则所抽得的图形既是中心对称图形又是轴对称图形的概率为_______.
学科内知识点融合
无理数
轴对称、中心对称图形
5.小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中
只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个
图案中有3个正方体,第(3)个图案中有6个正方体,…按照此规律,从第(100)个图案所需正方体中
随机抽取一个正方体,抽到带“心”字正方体的概率是________.
应用概率
找规律
6. 圆周率π是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前,超级计算机已计算出的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从π的小数部分随机取出一个数字,估计数字是6的概率为________;
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有一幅是祖冲之的概率.(用画树状图或列表方法求解)
应用概率
数学史
7. 我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和如图1,ar+cq+bp是该三角形的顺序旋转和,ap+bq+cr是该三角形的逆序旋转和.已知某三角形的特征值如图2,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数z,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是_________.
应用概率
新定义
判断事件
概率
概率的计算
概率的应用
小结
用频率估计概率
列举法求概率
用面积求概率
一步概率
两步概率
三步概率
同学们,再见!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
