苏科版 九年级下册 统计与概率单元复习课 课件(共27张PPT)
文档属性
| 名称 | 苏科版 九年级下册 统计与概率单元复习课 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
统计与概率单元复习课
数据的收集
随机事件
数据概念:
总体与个体
随机抽样
列举法
用频率估计概率
直方图
数据的分析
平均数
众数
中位数
方差
概率
列表法
树状图法
频率
概率
知识结构
一、数据的收集
一、数据的收集
例题1.下列调查中,适宜采用全面调查方式的是( )
A. 旅客上飞机前的安全检查
B. 对广州市七年级学生身高现状的调查
C. 多某品牌食品安全的调查
D. 对一批灯管使用寿命的调查
A
例题分析
二、总体与个体
1.总体: 所要考查对象的全体
2.个体:组成总体的每一个考察对象
3.样本:从总体中抽取的一部分个体
4.样本容量:一个样本中包含个体的数量
5.简单随机抽样:在抽取样本的过程中,总体中的每一个个体都有相等的机会被
抽到,像这样的抽样方法是一种简单随机抽样。
例题2 今年我市有近4万名考生参加中考,为了解这些考生的数学成绩,从中抽取
1000名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这1000名考生是总体的一个样本
B.近4万名考生是总体
C.每位考生的数学成绩是个体
D.1000名学生是样本容量
C
二、总体与个体
例题分析
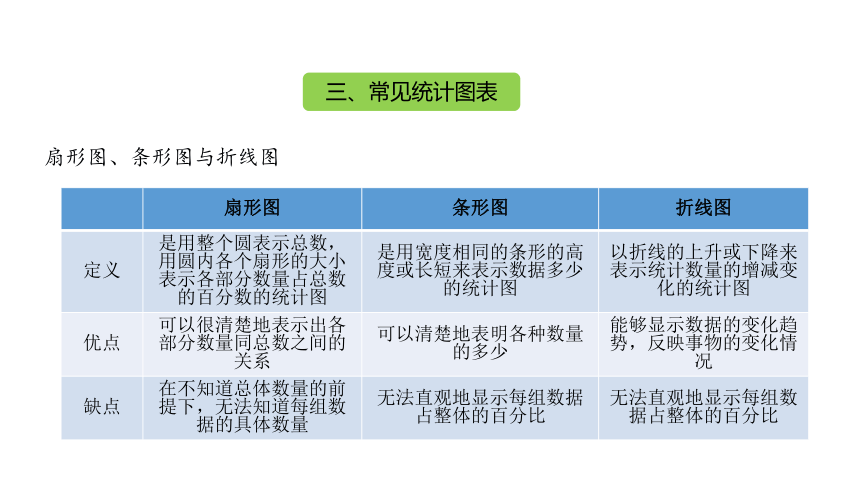
三、常见统计图表
扇形图、条形图与折线图
扇形图 条形图 折线图
定义 是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数的统计图 是用宽度相同的条形的高度或长短来表示数据多少的统计图 以折线的上升或下降来表示统计数量的增减变化的统计图
优点 可以很清楚地表示出各部分数量同总数之间的关系 可以清楚地表明各种数量的多少 能够显示数据的变化趋势,反映事物的变化情况
缺点 在不知道总体数量的前提下,无法知道每组数据的具体数量 无法直观地显示每组数据占整体的百分比 无法直观地显示每组数据占整体的百分比
三、常见统计图表
例题分析
例3 某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程.为了解学生对这四门课程的选择情况,学校从八年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出).
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生人数为▲名,补全条形统计图
(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占▲%;
(3)若该校八年级一共有1000名学生,试估计选择“刺绣”课程的
学生有多少名
三、常见统计图表
故答案为:10
四、平均数
1.平均数:把一组数据的总和除以这组数据的个数所得的商。
2.加权平均数:加权平均数即将各数值乘以相应的权数,然后求和得到
总体值,再除以总的单位数。
即:加权平均数的大小不仅取决于总体中各单位的数值(变量值)的大小,而且取决于各数值出现的次数(频数),由于各数值出现的次数对其在平均数中的影响起着权衡轻重的作用,因此叫做权数。
四、平均数
例题4 红星中学初三(2)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均
成绩为77分,则该班男、女生的人数之比为( )
A.1:2 B.2:1 C.3:2 D.2:3
例题5 为庆祝中国共产党建党一百周年,某校开展了主题为“我身边的共产党员”的演讲比赛.
比赛从演讲内容、演讲技巧、演讲效果三个方面打分,最终得分按4∶3∶3的比计算.若选手
甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分,80分,90分,则选手甲的
最终得分为________分.
C
例题分析
五、中位数和众数
1.中位数:按顺序排列的一组数据中居于中间位置的数;若数据个数为奇数,则称
处于中间位置的数为这组数据的中位数,若数据个数为偶数,则称中间
两个数据的平均数为这组数据的中位数。
2.众 数:一组数据中出现次数最多的数据成为这组数据的众数,
众数不一定是一个数字。
3.平均数、中位数、众数的区别与联系
五、中位数和众数
联系:
都是来描述数据集中趋势的统计量;都可用来反映数据的一般水平;都可用来作为一组数据的代表。
区别:
平均数是通过计算得到的,因此它会因每一个数据的变化而变化。
中位数是通过排序得到的,它不受最大、最小两个极端数值的影响。
中位数在一定程度上综合了平均数和中位数的优点,具有比较好的代表性。
众数也是数据的一种代表数,反映了一组数据的集中程度。
五、中位数和众数
在一组数据中,平均数和中位数都具有唯一性,但众数有时不具有唯一性。
在一组数据中,可能不止一个众数。
平均数说明的是整体的平均水平;众数说明的是生活中的多数情况;
中位数说明的是生活中的中等水平。
五、中位数和众数
例题分析
例题6
五、中位数和众数
六、方差
1.定义:样本中各数据与样本平均数的差的平方和的平均数叫做样本方差,
方差是一个衡量样本波动大小的量,也就是距离平均值得波动程度.
2.计算方法:一组数据x1,x2,x3……xn中,各组数据与它们的平均数x的差的平方
分别是(x1-x ) ,(x2-x ) ……(xn- x) ,然后求这些值的平均数,
即
方差越大,数据的波动越大,方差越小,数据的波动越小。
六、方差
例题分析
∵ 甲、丙、丁的射击成绩的平均数较大,且丁的方差<甲的方差<丙的方差,
∴ 成绩好且发挥稳定的运动员是丁.故选D.
七、随机事件与概率
七、随机事件与概率
例题8 “苏州市明天降水概率是30%”,对此消息下列说法中正确的是( )
A.苏州市明天将有30%的地区降水 B.苏州市明天将有30%的时间降水
C.苏州市明天降水的可能性较小 D.苏州市明天肯定不降水
例题9 下列事件属于随机事件的是( )
A.太阳从东边升起,西边落下 B.投掷硬币出现正面
C.火星上表面上都是液态水 D.鲸鱼可以在陆地上生活
C
B
八、用频率估计概率
1.在大量重复试验中,随着试验次数的增加,事件A的发生的频率会稳定于某个
常数p,我们称事件A发生的概率P(A)=p。
2.频率与概率
事件发生的概率是一个确定的值(理论值),而频率是不确定的(试验值),当试验次数较少时,频率的大小摇摆不定,当试验次数增大时,频率的大小波动变小,逐渐稳定在概率附近。
例如抛硬币记录硬币落地后正面朝上的次数,正面朝上的概率为0.5,但抛硬币次数较少时,正面朝上的频率不一定为一半,抛硬币次数越多时,正面朝上的频率会越接近0.5.
九、用列举法求概率
1.用列举法求概率的条件
(1)一次试验中,可能出现的结果只有有限个,
(2)一次试验中,各种结果出现的可能性大小相等.
2.列表法与树状图法
列表法:涉及两个因素并且可能出现的结果数目较多.
树状图法:涉及三个或更多因素时.
九、用列举法求概率
C
例题分析
九、用列举法求概率
例题分析
九、用列举法求概率
例题10 如图,用红、蓝两种颜色随机地对A,B,C三个区域分别进行涂色,每个区域必须涂色并且只能涂一种颜色,请用列举法(画树状图或列表)求A,C两个区域所涂颜色不相同的概率.
例题分析
九、用列举法求概率
例题分析
例题11 4张相同的卡片上分别写有数字0、1、-2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,
将卡片上的数字记录下来:再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是负数的概率为______;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果
为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗 为什么 (请用画树状图或列
表等方法说明理由)
统计与概率单元复习课
数据的收集
随机事件
数据概念:
总体与个体
随机抽样
列举法
用频率估计概率
直方图
数据的分析
平均数
众数
中位数
方差
概率
列表法
树状图法
频率
概率
知识结构
一、数据的收集
一、数据的收集
例题1.下列调查中,适宜采用全面调查方式的是( )
A. 旅客上飞机前的安全检查
B. 对广州市七年级学生身高现状的调查
C. 多某品牌食品安全的调查
D. 对一批灯管使用寿命的调查
A
例题分析
二、总体与个体
1.总体: 所要考查对象的全体
2.个体:组成总体的每一个考察对象
3.样本:从总体中抽取的一部分个体
4.样本容量:一个样本中包含个体的数量
5.简单随机抽样:在抽取样本的过程中,总体中的每一个个体都有相等的机会被
抽到,像这样的抽样方法是一种简单随机抽样。
例题2 今年我市有近4万名考生参加中考,为了解这些考生的数学成绩,从中抽取
1000名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这1000名考生是总体的一个样本
B.近4万名考生是总体
C.每位考生的数学成绩是个体
D.1000名学生是样本容量
C
二、总体与个体
例题分析
三、常见统计图表
扇形图、条形图与折线图
扇形图 条形图 折线图
定义 是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数的统计图 是用宽度相同的条形的高度或长短来表示数据多少的统计图 以折线的上升或下降来表示统计数量的增减变化的统计图
优点 可以很清楚地表示出各部分数量同总数之间的关系 可以清楚地表明各种数量的多少 能够显示数据的变化趋势,反映事物的变化情况
缺点 在不知道总体数量的前提下,无法知道每组数据的具体数量 无法直观地显示每组数据占整体的百分比 无法直观地显示每组数据占整体的百分比
三、常见统计图表
例题分析
例3 某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程.为了解学生对这四门课程的选择情况,学校从八年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出).
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生人数为▲名,补全条形统计图
(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占▲%;
(3)若该校八年级一共有1000名学生,试估计选择“刺绣”课程的
学生有多少名
三、常见统计图表
故答案为:10
四、平均数
1.平均数:把一组数据的总和除以这组数据的个数所得的商。
2.加权平均数:加权平均数即将各数值乘以相应的权数,然后求和得到
总体值,再除以总的单位数。
即:加权平均数的大小不仅取决于总体中各单位的数值(变量值)的大小,而且取决于各数值出现的次数(频数),由于各数值出现的次数对其在平均数中的影响起着权衡轻重的作用,因此叫做权数。
四、平均数
例题4 红星中学初三(2)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均
成绩为77分,则该班男、女生的人数之比为( )
A.1:2 B.2:1 C.3:2 D.2:3
例题5 为庆祝中国共产党建党一百周年,某校开展了主题为“我身边的共产党员”的演讲比赛.
比赛从演讲内容、演讲技巧、演讲效果三个方面打分,最终得分按4∶3∶3的比计算.若选手
甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分,80分,90分,则选手甲的
最终得分为________分.
C
例题分析
五、中位数和众数
1.中位数:按顺序排列的一组数据中居于中间位置的数;若数据个数为奇数,则称
处于中间位置的数为这组数据的中位数,若数据个数为偶数,则称中间
两个数据的平均数为这组数据的中位数。
2.众 数:一组数据中出现次数最多的数据成为这组数据的众数,
众数不一定是一个数字。
3.平均数、中位数、众数的区别与联系
五、中位数和众数
联系:
都是来描述数据集中趋势的统计量;都可用来反映数据的一般水平;都可用来作为一组数据的代表。
区别:
平均数是通过计算得到的,因此它会因每一个数据的变化而变化。
中位数是通过排序得到的,它不受最大、最小两个极端数值的影响。
中位数在一定程度上综合了平均数和中位数的优点,具有比较好的代表性。
众数也是数据的一种代表数,反映了一组数据的集中程度。
五、中位数和众数
在一组数据中,平均数和中位数都具有唯一性,但众数有时不具有唯一性。
在一组数据中,可能不止一个众数。
平均数说明的是整体的平均水平;众数说明的是生活中的多数情况;
中位数说明的是生活中的中等水平。
五、中位数和众数
例题分析
例题6
五、中位数和众数
六、方差
1.定义:样本中各数据与样本平均数的差的平方和的平均数叫做样本方差,
方差是一个衡量样本波动大小的量,也就是距离平均值得波动程度.
2.计算方法:一组数据x1,x2,x3……xn中,各组数据与它们的平均数x的差的平方
分别是(x1-x ) ,(x2-x ) ……(xn- x) ,然后求这些值的平均数,
即
方差越大,数据的波动越大,方差越小,数据的波动越小。
六、方差
例题分析
∵ 甲、丙、丁的射击成绩的平均数较大,且丁的方差<甲的方差<丙的方差,
∴ 成绩好且发挥稳定的运动员是丁.故选D.
七、随机事件与概率
七、随机事件与概率
例题8 “苏州市明天降水概率是30%”,对此消息下列说法中正确的是( )
A.苏州市明天将有30%的地区降水 B.苏州市明天将有30%的时间降水
C.苏州市明天降水的可能性较小 D.苏州市明天肯定不降水
例题9 下列事件属于随机事件的是( )
A.太阳从东边升起,西边落下 B.投掷硬币出现正面
C.火星上表面上都是液态水 D.鲸鱼可以在陆地上生活
C
B
八、用频率估计概率
1.在大量重复试验中,随着试验次数的增加,事件A的发生的频率会稳定于某个
常数p,我们称事件A发生的概率P(A)=p。
2.频率与概率
事件发生的概率是一个确定的值(理论值),而频率是不确定的(试验值),当试验次数较少时,频率的大小摇摆不定,当试验次数增大时,频率的大小波动变小,逐渐稳定在概率附近。
例如抛硬币记录硬币落地后正面朝上的次数,正面朝上的概率为0.5,但抛硬币次数较少时,正面朝上的频率不一定为一半,抛硬币次数越多时,正面朝上的频率会越接近0.5.
九、用列举法求概率
1.用列举法求概率的条件
(1)一次试验中,可能出现的结果只有有限个,
(2)一次试验中,各种结果出现的可能性大小相等.
2.列表法与树状图法
列表法:涉及两个因素并且可能出现的结果数目较多.
树状图法:涉及三个或更多因素时.
九、用列举法求概率
C
例题分析
九、用列举法求概率
例题分析
九、用列举法求概率
例题10 如图,用红、蓝两种颜色随机地对A,B,C三个区域分别进行涂色,每个区域必须涂色并且只能涂一种颜色,请用列举法(画树状图或列表)求A,C两个区域所涂颜色不相同的概率.
例题分析
九、用列举法求概率
例题分析
例题11 4张相同的卡片上分别写有数字0、1、-2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,
将卡片上的数字记录下来:再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是负数的概率为______;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果
为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗 为什么 (请用画树状图或列
表等方法说明理由)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
