第18章 勾股定理全章学案(共5课时)
文档属性
| 名称 | 第18章 勾股定理全章学案(共5课时) |  | |
| 格式 | zip | ||
| 文件大小 | 125.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-14 13:44:51 | ||
图片预览



文档简介
课题名称:勾股定理(1)
学习目标:
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。了解我国古代在勾股定理研究方面所取得的成就。
学习目标:经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。
学习重点:勾股定理的内容及证明。
学习难点:勾股定理的证明。
自助探究
1.1、2002年北京召开了被誉为数学界“奥运会”的国际数学家大会,
这就是当时采用的会徽. 你知道这个图案的名字吗?你知道它
的背景吗?你知道为什么会用它作为会徽吗?
2、相传2500年前,古希腊的数学家毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系. 请同学们也观察一下,看看能发现什么?
(1) 引导学生观察三个正方形之间的面积的关系;
(2) 引导学生把面积的关系转化为边的关系.
结论:等腰直角三角形三边的特殊关系:斜边的平方等于两直角边的平方和.
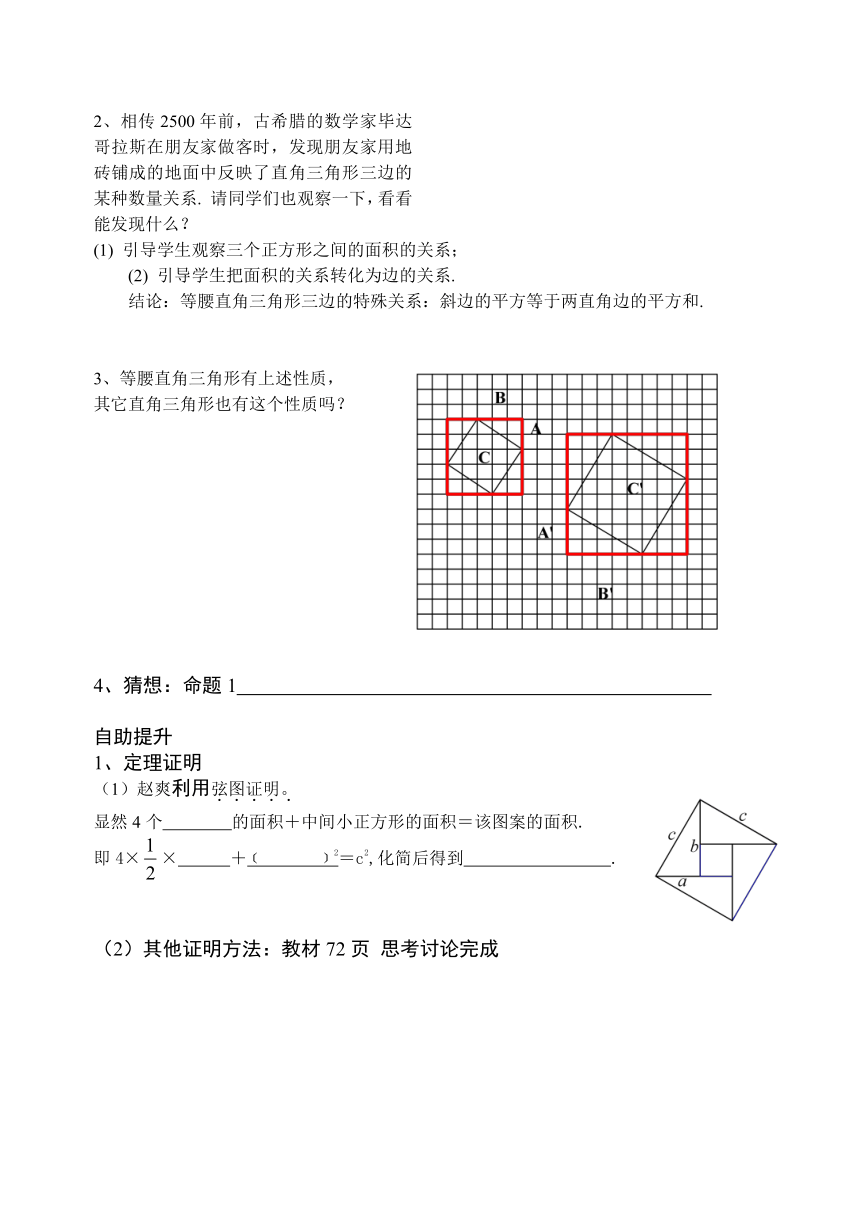
3、等腰直角三角形有上述性质,
其它直角三角形也有这个性质吗?
4、猜想:命题1
自助提升
1、定理证明
(1)赵爽利用弦图证明。
显然4个 的面积+中间小正方形的面积=该图案的面积.
即4×× +﹝ ﹞2=c2,化简后得到 .
(2)其他证明方法:教材72页 思考讨论完成
2、在Rt△ABC中,∠C=,AB=17,BC=8,求AC的长
3、Rt△ABC和以AB为边的正方形ABEF,∠ACB=90°,
AC=12,BC=5,则正方形的面积是______.
4、(1) 已知Rt△ABC中,∠C=90°,BC=6,AC=8,求AB.
(2) 已知Rt△ABC中,∠A=90°,AB=5,BC=6,求AC.
(3) 已知Rt△ABC中,∠B=90°,a,b,c分别是∠A,∠B,
∠C的对边,c∶a=3∶4,b=15,求a,c及斜边高线h.
5、如图1-1-4,所有的四边形都是正方形,所有的三角
形都是直角三角形,其中最大的正方形的边长为7cm,
则正方形A,B,C,D的面积之和是多少?
自助检测
1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是 ( )
2.斜边长为25 B.三角形的周长为25 C.斜边长为5 D.三角形面积为20
3.一直角三角形的斜边长比一条直角边长多2,另一直角边长为6,则斜边长为( )
A.4 B.8 C.10 D.12
4.直角三角形的两直角边的长分别是5和12,则其斜边上的高的长为( )
A.6 B.8 C. D.
5、已知,如图1-1-5,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求CF CE
小结与反思
这节课你学到了一些什么?你想进一步探究的问题是什么?
教学反思
§ 18.1 勾股定理(2)
一、学习目标
通过经历和体验,运用勾股定理解决一些实际问题的过程,进一步掌握勾股定理。
重点:勾股定理的应用。
难点:实际问题向数学问题的转化。
二、自助探究
1、一个门框的尺寸如图所示:
(1) 若有一块长3米,宽0.8米的薄木板,能否从门框内通过?
(2) 若有一块长3米,宽1.5米的薄木板,能否从门框内通过?
(3) 若有一块长3米,宽2.2米的薄木板,能否从门框内通过?
分析:(3) 木板的宽2.2米大于1米,所以横着不能从门框内通过.
木板的宽2.2米大于2米,所以竖着不能从门框内通过.
因为对角线AC的长度最大,所以只能试试斜着能否通过.
所以将实际问题转化为数学问题.
小结:此题是将实际为题转化为数学问题,从中抽象出Rt△ABC,并求出斜边AC的
2、例2、如图,一个3米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5米.如果梯子的顶端A沿墙下滑 0.5米,那么梯子底端B也外移0.5米吗?
(计算结果保留两位小数)
分析:要求出梯子的底端B是否也外移0.5米,实际就是求BD的长,而BD=OD-OB
3、一个大树高8米,折断后大树顶端落在离大树底端2米处,折断处离地面的高度是多少?
自助提升
1、已知:△ABC为等边三角形,AD⊥BC于D,AD=6. 求AC的长.
2、如果直角三角形的三边分别为3,5,a试求满足条件a的值?
3、以知正三角形ABC的边长为a,求△ABC的面积?
自助检测
1、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上
的高为 ( )
A、12 cm B、10 cm C、8 cm D、6 cm
2、如图,在⊿ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D。
求:(1)AC的长; (2)⊿ABC的面积; (3)CD的长。
3、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点
B处吃食,要爬行的最短路程(取3)是( )
A、20cm; B、10cm; C、14cm; D、无法确定.
4、若等腰直角三角形的斜边长为2,则它的直角边的长为 ,斜边上的高的长为 。
5、要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m,至少需要多长的梯子?(画出示意图)
6、小明的叔叔家承包了一个矩形鱼池,已知其面积为48m2,其对角线长为10m,为建栅栏,要计算这个矩形鱼池的周长,你能帮助小明算一算吗?
7、有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面。谁的深度和这根芦苇的长度分别是多少?
小结与反思
教后记
§ 18.1 勾股定理(3)
学习目标:1、熟练掌握勾股定理的内容
2、会用勾股定理解决简单的实际问题
3、利用勾股定理,能在数轴上表示无理数的点
重点:会在数轴上表示(n为正整数)
难点:综合运用
自助探究
1、勾股定理的内容_______________________
2、如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折
叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、6cm2 B、8cm2 C、10cm2 D、12cm2
3、13=9+4,即=+﹝ ﹞2;若以 和 为直角三角形的两直角边
长,则斜边长为。同理以 和 为直角三角形的两直角边长,则斜边长为
自助提升
1、探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
分析:(1)若能画出长为的线段,就能在数轴上画出表示的点.
(2)由勾股定理知,直角边为1的等腰Rt△,斜边为.因此在数轴上能表示的点.那么长为的线段能否是直角边为正整数的直角三角形的斜边呢?
在数轴上画出表示的点?(尺规作图)
2、如图:螺旋状图形是由若干个直角
三角形所组成的,其中①是直角边长为1的
等腰直角三角形。那么OA1= ,OA2= ,OA3= ,OA4= ,
OA5= ,OA6= ,OA7= ,…,OA14 = , …,OAn= .
思考:怎样在数轴上画出表示(n为正整数)的点?
自助检测:
1、在数轴上找出表示和-的点
2、已知:如图,在△ABC中,ADBC于D,AB=6,AC=4,BC=8,求BD,DC的长.
3、已知矩形ABCD沿直线BD折叠,使点C落在同一平面内C’处,BC’与AD交于点E,
AD=6,AB=4,求DE的长.
4、已知:如图,四边形ABCD中,AB=2,CD=1,∠A=60°, ∠B=∠D=90°. 求四边形ABCD的面积。
小结与反思
教后记
§18.2勾股定理的逆定理(1)
学习目标:1.掌握勾股定理的逆定理,并会用它判断一个三角形是不是直角三角形.
2.探究勾股定理的逆定理的证明方法.
3.理解原命题、逆命题、逆定理的概念及关系.
学习重点:勾股定理的逆定理及其实际应用.
学习难点:勾股定理逆定理的证明.
自助探究:
1、画以线段a,b, c. 为边的三角形并判断分别以上述a、b、c为边的三角形的形状.
⑴ a=3,b=4 c=5 ⑵ a=5,b=12 c=13 ⑶ a=7,b=24 c=25
2、猜想:命题2
该猜想的题设和结论与勾股定理的题设和结论正好 .
如果两个命题的题设、结论正好相反,那么这样的两个命题叫做 命题,若把其中一个叫做原命题,那么另一个叫做它的 命题.譬如:
①原命题:若a=b,则a2=b2;逆命题: .(正确吗?答 )
②原命题:对顶角相等;逆命题: . (正确吗?答 )
由此可见:原命题正确,它的逆命可能 也可能 .正确的命题叫真命题,不正确的命题叫假命题
自助提升:
1、命题2:如果三角形的三边长、、满足,那么这个三角形是直角三角形.
已知:在△ABC中,AB=c,BC=a,CA=b,且
求证:∠C=90°
思路:构造法——构造一个直角三角形,使它与原三角形全等,利用对应角相等来证明.
通过证明,我发现勾股定理的逆题是 的,它也是一个 ,我们把它叫做勾股定理的 .
小结注:(1)每一个命题都有逆命题.
(2)一个命题的逆命题是否成立与原命题是否成立没有因果关系.
(3)每个定理都有逆命题,但不一定都有逆定理.
2、例1、判断由线段a,b,c组成的△ABC是不是直角三角形.
(1) a=40,b=41,c=9
(2) a=13,b=14,c=15
(3) a∶b∶c=∶3∶2
(4) ,,(n>1且n为整数)
分析:①首先确定最大边;
②验证最大边的平方与最短的两边平方和是否相等
3、勾股数(P75)
能够成为直角三角形三条边长的三个正整数,称为勾股数.
如果a、b、c是一组勾股数,m>0,那么ma,mb,mc也是一组勾股数
自助检测:
1、 分别以下列四组数为一个三角形的边长:(1)3,4,5; (2)5,12,13;
(3)8,15,17; (4)4,5,6. 其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
2、 三角形的三边长分别为a2+b2、2ab、a2-b2(a、b都是正整数),则这个三角形是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
3、已知两条线段的长为5cm和12cm,当第三条线段的长为???????????????? cm时,这三条线段能组成一个直角三角形。
4、一个零件的形状如左图所示,按规定这个零件中∠A
和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如右
图所示,这个零件符合要求吗?
小结与反思
目前判定三角形是直角三角形的方法有哪些?
教后记
§18.2勾股定理的逆定理(2)
学习目标:
1、进一步掌握勾股定理的逆定理,并能运用勾股定理的逆定理解决有关问题。
2、在探究活动过程中,经历知识的发生、发展与形成的过程. 培养敢于实践、勇于发现、大胆探索、合作创新的精神,增强学好数学、用好数学的信心和勇气.
学习重点:勾股定理的逆定理及其实际应用.
学习难点:勾股定理逆定理的灵活应用.
自助探究:
1、勾股定理是直角三角形的 定理;它的逆定理是直角三角形的 定理.
2、请写出三组不同的勾股数: 、 、 .
3、测得一块三角形麦田三边长分别为9m,12m,15m,则这块麦田的面积为________㎡。
4、借助三角板画出如下方位角所确定的射线:
①南偏东30°;②西南方向;③北偏西60°.
自助提升:
1、例1、某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里. 如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
分析:“远航”号航行方向已知,只要求出“海天”号与它的航向的夹角就可以知道“海天”号的航行方向.
2、例2、已知在△ABC中,D是BC边上的一点,若AB=10,BD=6,AD=8,AC=17,求S△ABC.
3、一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
自助检测:
1、一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为 ,此三角形的形状为 。
2、已知:如图,四边形ABCD中,AB=3,BC=4,CD=5,AD=,
∠B=90°,求四边形ABCD的面积.
3、如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西n°,问:甲巡逻艇的航向?
4、已知:如图,在正方形ABCD中,F为AD上一点,且DF=AD,E是CD的中点.
求证:BE⊥EF
思路:(1)要证BE⊥EF,可证∠BEF是Rt∠.
(2)由勾股逆定理想到:只要证即可.
(3)因此可在Rt△ABF,Rt△DEF,Rt△BCE中分别计算出,,.
小结与反思
学习目标:
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。了解我国古代在勾股定理研究方面所取得的成就。
学习目标:经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。
学习重点:勾股定理的内容及证明。
学习难点:勾股定理的证明。
自助探究
1.1、2002年北京召开了被誉为数学界“奥运会”的国际数学家大会,
这就是当时采用的会徽. 你知道这个图案的名字吗?你知道它
的背景吗?你知道为什么会用它作为会徽吗?
2、相传2500年前,古希腊的数学家毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系. 请同学们也观察一下,看看能发现什么?
(1) 引导学生观察三个正方形之间的面积的关系;
(2) 引导学生把面积的关系转化为边的关系.
结论:等腰直角三角形三边的特殊关系:斜边的平方等于两直角边的平方和.
3、等腰直角三角形有上述性质,
其它直角三角形也有这个性质吗?
4、猜想:命题1
自助提升
1、定理证明
(1)赵爽利用弦图证明。
显然4个 的面积+中间小正方形的面积=该图案的面积.
即4×× +﹝ ﹞2=c2,化简后得到 .
(2)其他证明方法:教材72页 思考讨论完成
2、在Rt△ABC中,∠C=,AB=17,BC=8,求AC的长
3、Rt△ABC和以AB为边的正方形ABEF,∠ACB=90°,
AC=12,BC=5,则正方形的面积是______.
4、(1) 已知Rt△ABC中,∠C=90°,BC=6,AC=8,求AB.
(2) 已知Rt△ABC中,∠A=90°,AB=5,BC=6,求AC.
(3) 已知Rt△ABC中,∠B=90°,a,b,c分别是∠A,∠B,
∠C的对边,c∶a=3∶4,b=15,求a,c及斜边高线h.
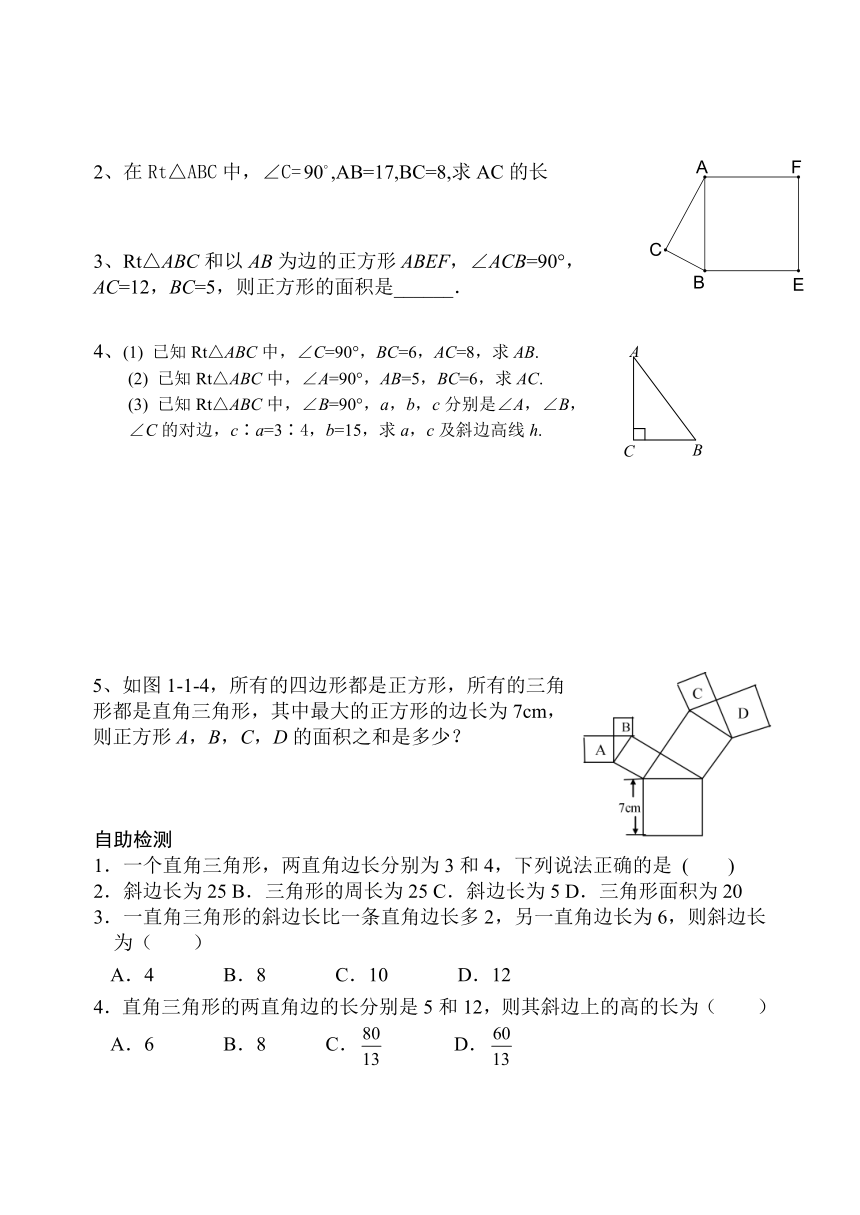
5、如图1-1-4,所有的四边形都是正方形,所有的三角
形都是直角三角形,其中最大的正方形的边长为7cm,
则正方形A,B,C,D的面积之和是多少?
自助检测
1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是 ( )
2.斜边长为25 B.三角形的周长为25 C.斜边长为5 D.三角形面积为20
3.一直角三角形的斜边长比一条直角边长多2,另一直角边长为6,则斜边长为( )
A.4 B.8 C.10 D.12
4.直角三角形的两直角边的长分别是5和12,则其斜边上的高的长为( )
A.6 B.8 C. D.
5、已知,如图1-1-5,折叠长方形(四个角都是直角,对边相等)的一边AD使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求CF CE
小结与反思
这节课你学到了一些什么?你想进一步探究的问题是什么?
教学反思
§ 18.1 勾股定理(2)
一、学习目标
通过经历和体验,运用勾股定理解决一些实际问题的过程,进一步掌握勾股定理。
重点:勾股定理的应用。
难点:实际问题向数学问题的转化。
二、自助探究
1、一个门框的尺寸如图所示:
(1) 若有一块长3米,宽0.8米的薄木板,能否从门框内通过?
(2) 若有一块长3米,宽1.5米的薄木板,能否从门框内通过?
(3) 若有一块长3米,宽2.2米的薄木板,能否从门框内通过?
分析:(3) 木板的宽2.2米大于1米,所以横着不能从门框内通过.
木板的宽2.2米大于2米,所以竖着不能从门框内通过.
因为对角线AC的长度最大,所以只能试试斜着能否通过.
所以将实际问题转化为数学问题.
小结:此题是将实际为题转化为数学问题,从中抽象出Rt△ABC,并求出斜边AC的
2、例2、如图,一个3米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5米.如果梯子的顶端A沿墙下滑 0.5米,那么梯子底端B也外移0.5米吗?
(计算结果保留两位小数)
分析:要求出梯子的底端B是否也外移0.5米,实际就是求BD的长,而BD=OD-OB
3、一个大树高8米,折断后大树顶端落在离大树底端2米处,折断处离地面的高度是多少?
自助提升
1、已知:△ABC为等边三角形,AD⊥BC于D,AD=6. 求AC的长.
2、如果直角三角形的三边分别为3,5,a试求满足条件a的值?
3、以知正三角形ABC的边长为a,求△ABC的面积?
自助检测
1、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上
的高为 ( )
A、12 cm B、10 cm C、8 cm D、6 cm
2、如图,在⊿ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D。
求:(1)AC的长; (2)⊿ABC的面积; (3)CD的长。
3、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点
B处吃食,要爬行的最短路程(取3)是( )
A、20cm; B、10cm; C、14cm; D、无法确定.
4、若等腰直角三角形的斜边长为2,则它的直角边的长为 ,斜边上的高的长为 。
5、要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m,至少需要多长的梯子?(画出示意图)
6、小明的叔叔家承包了一个矩形鱼池,已知其面积为48m2,其对角线长为10m,为建栅栏,要计算这个矩形鱼池的周长,你能帮助小明算一算吗?
7、有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面。谁的深度和这根芦苇的长度分别是多少?
小结与反思
教后记
§ 18.1 勾股定理(3)
学习目标:1、熟练掌握勾股定理的内容
2、会用勾股定理解决简单的实际问题
3、利用勾股定理,能在数轴上表示无理数的点
重点:会在数轴上表示(n为正整数)
难点:综合运用
自助探究
1、勾股定理的内容_______________________
2、如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折
叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、6cm2 B、8cm2 C、10cm2 D、12cm2
3、13=9+4,即=+﹝ ﹞2;若以 和 为直角三角形的两直角边
长,则斜边长为。同理以 和 为直角三角形的两直角边长,则斜边长为
自助提升
1、探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
分析:(1)若能画出长为的线段,就能在数轴上画出表示的点.
(2)由勾股定理知,直角边为1的等腰Rt△,斜边为.因此在数轴上能表示的点.那么长为的线段能否是直角边为正整数的直角三角形的斜边呢?
在数轴上画出表示的点?(尺规作图)
2、如图:螺旋状图形是由若干个直角
三角形所组成的,其中①是直角边长为1的
等腰直角三角形。那么OA1= ,OA2= ,OA3= ,OA4= ,
OA5= ,OA6= ,OA7= ,…,OA14 = , …,OAn= .
思考:怎样在数轴上画出表示(n为正整数)的点?
自助检测:
1、在数轴上找出表示和-的点
2、已知:如图,在△ABC中,ADBC于D,AB=6,AC=4,BC=8,求BD,DC的长.
3、已知矩形ABCD沿直线BD折叠,使点C落在同一平面内C’处,BC’与AD交于点E,
AD=6,AB=4,求DE的长.
4、已知:如图,四边形ABCD中,AB=2,CD=1,∠A=60°, ∠B=∠D=90°. 求四边形ABCD的面积。
小结与反思
教后记
§18.2勾股定理的逆定理(1)
学习目标:1.掌握勾股定理的逆定理,并会用它判断一个三角形是不是直角三角形.
2.探究勾股定理的逆定理的证明方法.
3.理解原命题、逆命题、逆定理的概念及关系.
学习重点:勾股定理的逆定理及其实际应用.
学习难点:勾股定理逆定理的证明.
自助探究:
1、画以线段a,b, c. 为边的三角形并判断分别以上述a、b、c为边的三角形的形状.
⑴ a=3,b=4 c=5 ⑵ a=5,b=12 c=13 ⑶ a=7,b=24 c=25
2、猜想:命题2
该猜想的题设和结论与勾股定理的题设和结论正好 .
如果两个命题的题设、结论正好相反,那么这样的两个命题叫做 命题,若把其中一个叫做原命题,那么另一个叫做它的 命题.譬如:
①原命题:若a=b,则a2=b2;逆命题: .(正确吗?答 )
②原命题:对顶角相等;逆命题: . (正确吗?答 )
由此可见:原命题正确,它的逆命可能 也可能 .正确的命题叫真命题,不正确的命题叫假命题
自助提升:
1、命题2:如果三角形的三边长、、满足,那么这个三角形是直角三角形.
已知:在△ABC中,AB=c,BC=a,CA=b,且
求证:∠C=90°
思路:构造法——构造一个直角三角形,使它与原三角形全等,利用对应角相等来证明.
通过证明,我发现勾股定理的逆题是 的,它也是一个 ,我们把它叫做勾股定理的 .
小结注:(1)每一个命题都有逆命题.
(2)一个命题的逆命题是否成立与原命题是否成立没有因果关系.
(3)每个定理都有逆命题,但不一定都有逆定理.
2、例1、判断由线段a,b,c组成的△ABC是不是直角三角形.
(1) a=40,b=41,c=9
(2) a=13,b=14,c=15
(3) a∶b∶c=∶3∶2
(4) ,,(n>1且n为整数)
分析:①首先确定最大边;
②验证最大边的平方与最短的两边平方和是否相等
3、勾股数(P75)
能够成为直角三角形三条边长的三个正整数,称为勾股数.
如果a、b、c是一组勾股数,m>0,那么ma,mb,mc也是一组勾股数
自助检测:
1、 分别以下列四组数为一个三角形的边长:(1)3,4,5; (2)5,12,13;
(3)8,15,17; (4)4,5,6. 其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
2、 三角形的三边长分别为a2+b2、2ab、a2-b2(a、b都是正整数),则这个三角形是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
3、已知两条线段的长为5cm和12cm,当第三条线段的长为???????????????? cm时,这三条线段能组成一个直角三角形。
4、一个零件的形状如左图所示,按规定这个零件中∠A
和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如右
图所示,这个零件符合要求吗?
小结与反思
目前判定三角形是直角三角形的方法有哪些?
教后记
§18.2勾股定理的逆定理(2)
学习目标:
1、进一步掌握勾股定理的逆定理,并能运用勾股定理的逆定理解决有关问题。
2、在探究活动过程中,经历知识的发生、发展与形成的过程. 培养敢于实践、勇于发现、大胆探索、合作创新的精神,增强学好数学、用好数学的信心和勇气.
学习重点:勾股定理的逆定理及其实际应用.
学习难点:勾股定理逆定理的灵活应用.
自助探究:
1、勾股定理是直角三角形的 定理;它的逆定理是直角三角形的 定理.
2、请写出三组不同的勾股数: 、 、 .
3、测得一块三角形麦田三边长分别为9m,12m,15m,则这块麦田的面积为________㎡。
4、借助三角板画出如下方位角所确定的射线:
①南偏东30°;②西南方向;③北偏西60°.
自助提升:
1、例1、某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里. 如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
分析:“远航”号航行方向已知,只要求出“海天”号与它的航向的夹角就可以知道“海天”号的航行方向.
2、例2、已知在△ABC中,D是BC边上的一点,若AB=10,BD=6,AD=8,AC=17,求S△ABC.
3、一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
自助检测:
1、一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为 ,此三角形的形状为 。
2、已知:如图,四边形ABCD中,AB=3,BC=4,CD=5,AD=,
∠B=90°,求四边形ABCD的面积.
3、如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西n°,问:甲巡逻艇的航向?
4、已知:如图,在正方形ABCD中,F为AD上一点,且DF=AD,E是CD的中点.
求证:BE⊥EF
思路:(1)要证BE⊥EF,可证∠BEF是Rt∠.
(2)由勾股逆定理想到:只要证即可.
(3)因此可在Rt△ABF,Rt△DEF,Rt△BCE中分别计算出,,.
小结与反思
