沪教版五年级下学期数学面积的估测(教案)
文档属性
| 名称 | 沪教版五年级下学期数学面积的估测(教案) |
|
|
| 格式 | zip | ||
| 文件大小 | 29.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-28 00:00:00 | ||
图片预览

文档简介
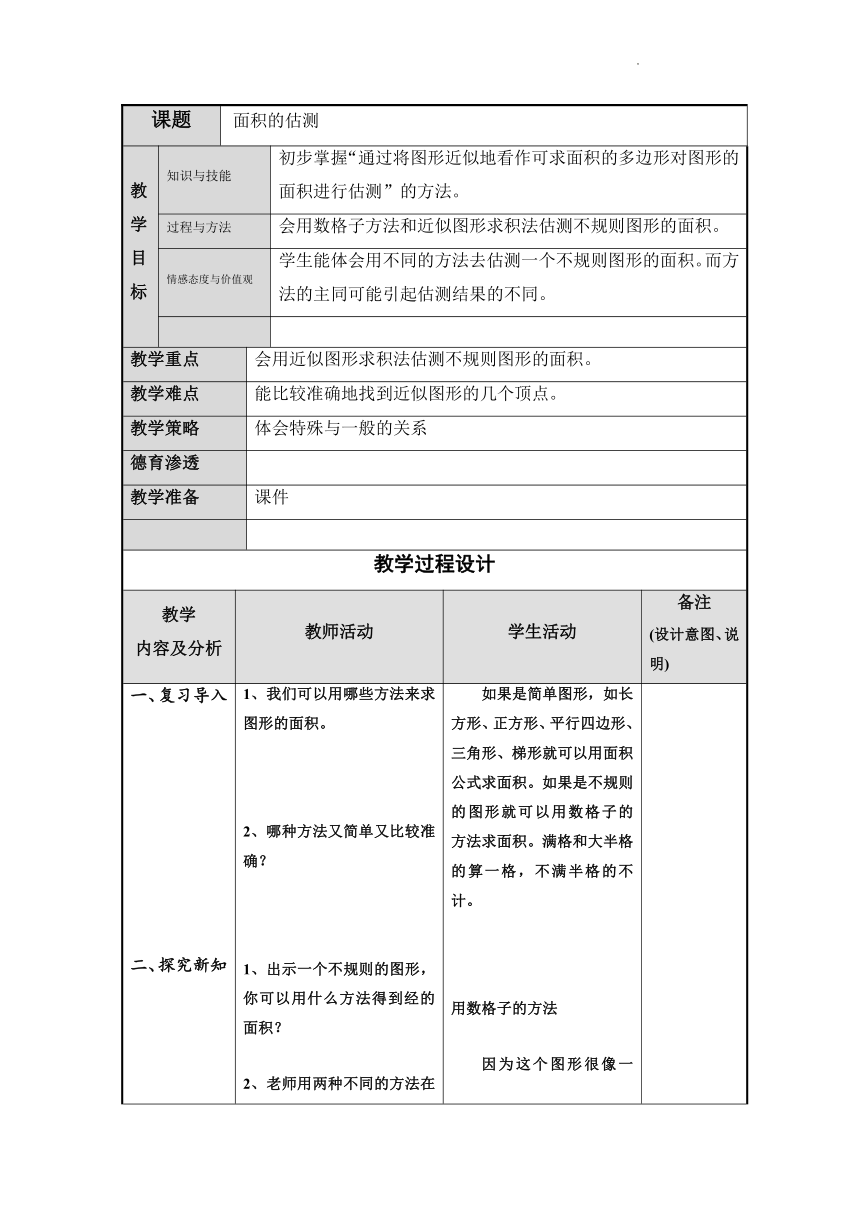
课题 面积的估测
教学目标 知识与技能 初步掌握“通过将图形近似地看作可求面积的多边形对图形的面积进行估测”的方法。
过程与方法 会用数格子方法和近似图形求积法估测不规则图形的面积。
情感态度与价值观 学生能体会用不同的方法去估测一个不规则图形的面积。而方法的主同可能引起估测结果的不同。
教学重点 会用近似图形求积法估测不规则图形的面积。
教学难点 能比较准确地找到近似图形的几个顶点。
教学策略 体会特殊与一般的关系
德育渗透
教学准备 课件
教学过程设计
教学 内容及分析 教师活动 学生活动 备注 (设计意图、说明)
一、复习导入 二、探究新知 三、学生练习 四、课堂小结 五、课堂作业 1、我们可以用哪些方法来求图形的面积。 2、哪种方法又简单又比较准确? 1、出示一个不规则的图形,你可以用什么方法得到经的面积? 2、老师用两种不同的方法在电脑上演示。 (重点让学生找出三角形三个顶点的位置) 3、两个结果为什么不同。 4、用不同的方法进行估测,结果可能会不一样。 第三题用边长为10米的格子,所以有两种方法可以选择 1、先用正确的单位来表示上底下底和高。再求面积。 2、先求出面积共有多少格,再按每格100平方米计算出图形面积。 当一个不规则图形计算面积时,我们可以根据图形的的特点近似看作一个或几个简单图形,运用面积公式,估测出它的面积。 练习册 如果是简单图形,如长方形、正方形、平行四边形、三角形、梯形就可以用面积公式求面积。如果是不规则的图形就可以用数格子的方法求面积。满格和大半格的算一格,不满半格的不计。 用数格子的方法 因为这个图形很像一个三角形所以可以看作三角形,利用公式求面积。 学生口答计算过程和结果。 发现用面积公式计算速度快。但必须找到合适的顶点和相应的条件。 P5练一练 学生能体会用不同的方法去估测一个不规则图形的面积的优势
教学目标 知识与技能 初步掌握“通过将图形近似地看作可求面积的多边形对图形的面积进行估测”的方法。
过程与方法 会用数格子方法和近似图形求积法估测不规则图形的面积。
情感态度与价值观 学生能体会用不同的方法去估测一个不规则图形的面积。而方法的主同可能引起估测结果的不同。
教学重点 会用近似图形求积法估测不规则图形的面积。
教学难点 能比较准确地找到近似图形的几个顶点。
教学策略 体会特殊与一般的关系
德育渗透
教学准备 课件
教学过程设计
教学 内容及分析 教师活动 学生活动 备注 (设计意图、说明)
一、复习导入 二、探究新知 三、学生练习 四、课堂小结 五、课堂作业 1、我们可以用哪些方法来求图形的面积。 2、哪种方法又简单又比较准确? 1、出示一个不规则的图形,你可以用什么方法得到经的面积? 2、老师用两种不同的方法在电脑上演示。 (重点让学生找出三角形三个顶点的位置) 3、两个结果为什么不同。 4、用不同的方法进行估测,结果可能会不一样。 第三题用边长为10米的格子,所以有两种方法可以选择 1、先用正确的单位来表示上底下底和高。再求面积。 2、先求出面积共有多少格,再按每格100平方米计算出图形面积。 当一个不规则图形计算面积时,我们可以根据图形的的特点近似看作一个或几个简单图形,运用面积公式,估测出它的面积。 练习册 如果是简单图形,如长方形、正方形、平行四边形、三角形、梯形就可以用面积公式求面积。如果是不规则的图形就可以用数格子的方法求面积。满格和大半格的算一格,不满半格的不计。 用数格子的方法 因为这个图形很像一个三角形所以可以看作三角形,利用公式求面积。 学生口答计算过程和结果。 发现用面积公式计算速度快。但必须找到合适的顶点和相应的条件。 P5练一练 学生能体会用不同的方法去估测一个不规则图形的面积的优势
