四川省成都市新津中学2013届高三2月月考数学(文)试题
文档属性
| 名称 | 四川省成都市新津中学2013届高三2月月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 247.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-14 00:00:00 | ||
图片预览




文档简介
新津中学高三数学(文)2月月考试题
参考公式:球体的表面积公式,其中为球体的半径
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.若复数,则a + b =( )
A.0 B.1 C.-1 D.2
2.函数的定义域是 ( )
A. B. C. D.
3.已知函数,则函数的零点个数为( )
A、1 B、2 C、3 D、4
4.已知是等差数列,,,则过点的直线的斜率为( )
A.4 B. C.-4 D.-14
5.已知向量,,且,则实数的值为( )
A. B. C. D.
6. 过点与圆相交的所有直线中,被圆截得的弦最长时的直线方程是( )
A. B. C. D.
7. 已知F1、F2是椭圆+=1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
A. B. C. D.
8.右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是( )
A. B.
C. D.
9.设向量与的夹角为,定义与的“向量积”:是一个向量,它的模,若,则( )
A. B.2 C. D.4
10.已知函数:,其中:,记函数满足条件:为事件为A,则事件A发生的概率为( )
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,满分25分
11. 命题“”的否定是_________________
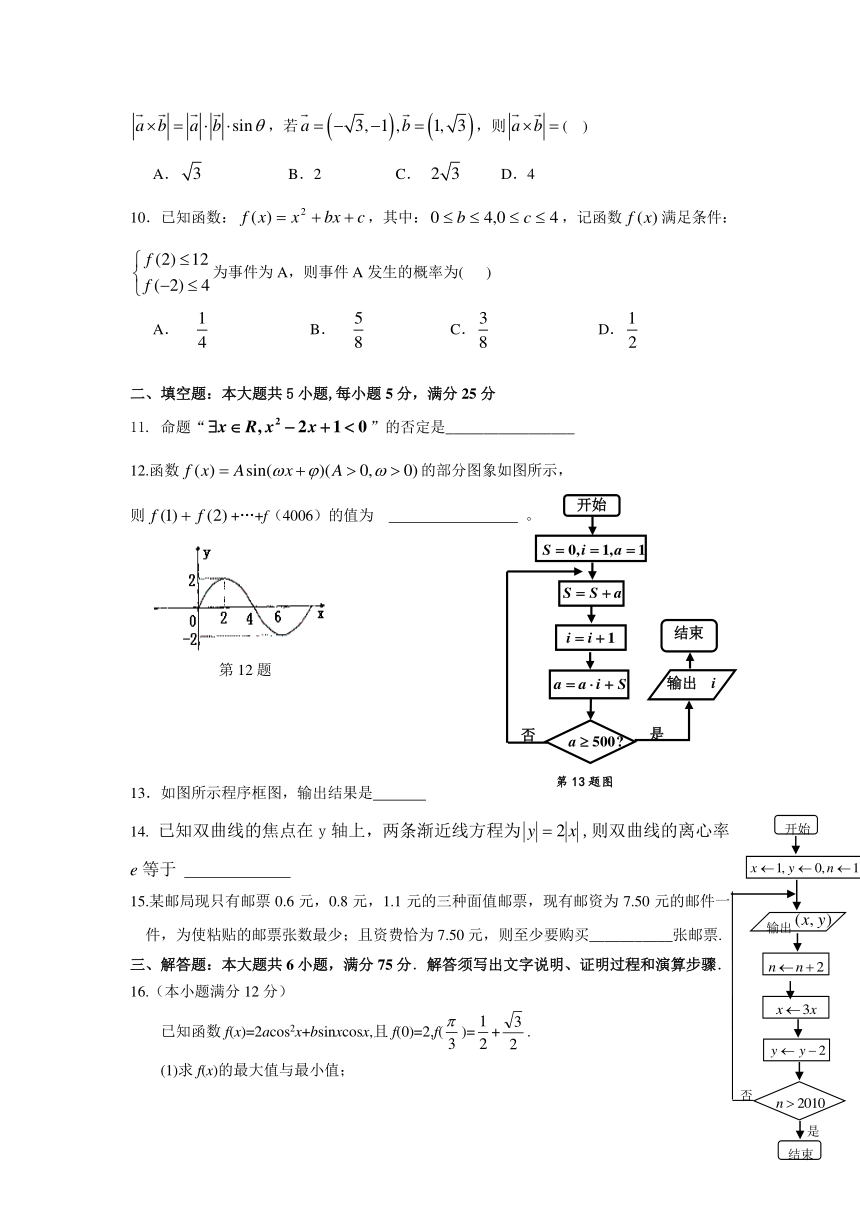
12.函数的部分图象如图所示,
则+…+f(4006)的值为 。
13.如图所示程序框图,输出结果是
14. 已知双曲线的焦点在y轴上,两条渐近线方程为,则双曲线的离心率e等于
15.某邮局现只有邮票0.6元,0.8元,1.1元的三种面值邮票,现有邮资为7.50元的邮件一件,为使粘贴的邮票张数最少;且资费恰为7.50元,则至少要购买___________张邮票.
三、解答题:本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知函数f(x)=2acos2x+bsinxcosx,且f(0)=2,f()=+.
(1)求f(x)的最大值与最小值;
(2)若α-β≠kπ,k∈Z,且f(α)=f(β),求tan(α+β)的值.
17.(本小题满分12分)
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费200元.
(1)当每辆车的月租金为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少元?
18.(本小题满分12分)
如图5,已知平面,平面,△为等边
三角形,,为的中点.
(1)求证:平面;
(2)求证:平面平面;
19.(本小题满分12分)
已知数列满足:.
(1)求证:数列为等差数列; (2)求数列的通项公式;
(3)令,证明:.
20.(本小题满分13分)
已知圆:及定点,点是圆上的动点,点在上,点在上,且满足=2,
·=. (1)若,求点的轨迹的方程;
(2)若动圆和(1)中所求轨迹相交于不同两点,是否存在一组正实数,使得直线垂直平分线段,若存在,求出这组正实数;若不存在,说明理由.
21.(本小题满分14分)
已知函数的图象过点,且在内单调递减,在上单调递增
(1)求的解析式;
(2)若对于任意的,不等式恒成立,试问这样的是否存在.若存在,请求出的范围,若不存在,说明理由;
新津中学高三数学(文)2月月考试题
一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
C
A
B
C
B
C
B
D
选择题参考答案:
1.解:,选B.
2.解:由对数函数的定义域可得到:
即选C
3. 当;
当,共3个零点,选C
4.,由,,化简可以得到公差,选A
5. 由,则,选B
6.易知圆的直径所在直线符合题意,由圆心,直线的斜率,则根据点斜式方程为;,选C
7.由椭圆的定义可知:,则=16-5=11
选B
8.从三视图中可以看出该几何体是半球体,则表面积,选C
9. 由,则,则,故,选B
10.本题为线性规划和几何概型的综合题,由条件可得到:
,以为横纵坐标作出满足条件的平面区域;
而总面积是由决定的正方形区域
面积之比为,选D
二、填空题:本大题查基本知识和基本运算,体现选择性.共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.
11.
12.
13. ,
14.
15.
填空题参考答案:
11. ;本题考察的对立性
12.由统计知识,该组数据的平均值点,代入方程得到
13.根据框图知识可得到点符合的特征为,由;又因为2010之前的奇数共有1005个,则输出的组数为1005组
14.设半径为,根据平面几何知识(切割线定理)
有,
代入数值可得
15.将曲线化简;得到,作出图像可观察到
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知坐标平面上三点,,.
(1)若(O为原点),求向量与夹角的大小;
解:(1)∵,
,
∴, …………… 2分
∴. …………… 4分
又,,设与的夹角为,则:
,
∴与的夹角为或. ………… 7分
(2)若,求的值.
解 :,
, ……… 9分
由,∴,
可得,① ………… 11分
∴,∴,
…………12分
17.(本小题满分12分)
甲、乙两人参加普法知识竞赛,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙两人依次各抽一题。
① 甲抽到选择题,乙抽到判断题的概率是多少?
解:(1)记 “甲抽到选择题,乙抽到判断题”为事件A, ……2分
甲抽到选择题有6种抽法,乙抽到判断题有4种抽法,
所以事件A的基本事件数为 ………………4分
∴ ……6分
② 甲、乙二人中至少有一人抽到选择题的概率是多少?
解:(2)记“甲、乙两人都抽到判断题”为事件B,
“至少一人抽到选择题”为事件C,
则B含基本事件数为 …………8分
由古典概率公式得 ………10分
由对立事件的性质可得 ……12分
18.(本小题满分14分)
如图5,已知平面,平面,
△为等边三角形,,
为的中点.
(1)求证:平面;
证明:(1) 证:取的中点,连结.
∵为的中点,
∴且.
∵平面,平面,
∴,∴.
又,∴. ………… 4分
∴四边形为平行四边形,则.
∵平面,平面,
∴平面. ………… 7分
(2)求证:平面平面;
证:∵为等边三角形,为的中点,
∴ ∵平面, ………… 9分
平面,∴.
又,故平面.………… 11分
∵,∴平面. ∵平面,
∴平面平面. …………14分
19.(本小题满分14分)
已知数列满足:.
(1)求证:数列为等差数列;
证明:,
=
==. ………………3分
数列为等差数列. ………………4分
(2)求数列的通项公式;
解: 由(1)得,为等差数列,公差为1,
首项为. ………………6分
(. ………………8分
.………9分
(3)令,证明:.
, ………10分
. ………11分
. ………12分
当时,
…………13分
当时,
综上所述:. ………14分
20.(本小题满分14分)
已知圆:及定点,点是圆上的动点,点在上,点在上,且满足
=2, ·=.
(1)若,求点的轨迹的方程;
解:(1)点为的中点,
又,
或点与点重合.∴ …………2分
又
∴点的轨迹是以为焦点的椭圆,
且,
∴的轨迹方程是 …………6分
(2)若动圆和(1)中所求轨迹相交于不同两点,是否存在一组正实数,使得直线垂直平分线段,若存在,求出这组正实数;若不存在,说明理由.
解:不存在这样一组正实数,下面证明: ……7分
由题意,若存在这样的一组正实数,当直线的斜率存在时,
设之为,故直线的方程为:
,设,中点,
则,两式相减得:.…………9分
注意到,
且 ,
则 , ②
又点在直线上,,
代入②式得:.
因为弦的中点在⑴所给椭圆内,故,
这与矛盾,所以所求这组正实数不存在. …………13分
当直线的斜率不存在时,直线的方程为,
则此时,
代入①式得,这与是不同两点矛盾.
综上,所求的这组正实数不存在. ………14分
21.(本小题满分14分)
对于定义域为D的函数,若同时满足下列条件:①在D内单调递增或单调递减;②存在区间[],使在[]上的值域为[];那么把()叫闭函数。
(Ⅰ)求闭函数符合条件②的区间[];
解:(Ⅰ)由题意,在[]上递减,
则
解得…………3分
所以,所求的区间为[-1,1] ………………………4分
(Ⅱ)判断函数是否为闭函数?并说明理由;
解:取则,
即不是上的减函数。…………6分
取
,
即不是上的增函数 …………8分
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。 ---------9分
(Ⅲ)若是闭函数,求实数的取值范围。
解:若是闭函数,则存在区间[],
在区间[]上,函数的值域为[],
即,为方程
的两个实数根,…………10分
即方程有两个不等的实根。
当时,有,
解得 …………12分
当时,有,无解 ……13分
综上所述, -----------14分
参考公式:球体的表面积公式,其中为球体的半径
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.若复数,则a + b =( )
A.0 B.1 C.-1 D.2
2.函数的定义域是 ( )
A. B. C. D.
3.已知函数,则函数的零点个数为( )
A、1 B、2 C、3 D、4
4.已知是等差数列,,,则过点的直线的斜率为( )
A.4 B. C.-4 D.-14
5.已知向量,,且,则实数的值为( )
A. B. C. D.
6. 过点与圆相交的所有直线中,被圆截得的弦最长时的直线方程是( )
A. B. C. D.
7. 已知F1、F2是椭圆+=1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
A. B. C. D.
8.右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是( )
A. B.
C. D.
9.设向量与的夹角为,定义与的“向量积”:是一个向量,它的模,若,则( )
A. B.2 C. D.4
10.已知函数:,其中:,记函数满足条件:为事件为A,则事件A发生的概率为( )
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,满分25分
11. 命题“”的否定是_________________
12.函数的部分图象如图所示,
则+…+f(4006)的值为 。
13.如图所示程序框图,输出结果是
14. 已知双曲线的焦点在y轴上,两条渐近线方程为,则双曲线的离心率e等于
15.某邮局现只有邮票0.6元,0.8元,1.1元的三种面值邮票,现有邮资为7.50元的邮件一件,为使粘贴的邮票张数最少;且资费恰为7.50元,则至少要购买___________张邮票.
三、解答题:本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知函数f(x)=2acos2x+bsinxcosx,且f(0)=2,f()=+.
(1)求f(x)的最大值与最小值;
(2)若α-β≠kπ,k∈Z,且f(α)=f(β),求tan(α+β)的值.
17.(本小题满分12分)
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费200元.
(1)当每辆车的月租金为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少元?
18.(本小题满分12分)
如图5,已知平面,平面,△为等边
三角形,,为的中点.
(1)求证:平面;
(2)求证:平面平面;
19.(本小题满分12分)
已知数列满足:.
(1)求证:数列为等差数列; (2)求数列的通项公式;
(3)令,证明:.
20.(本小题满分13分)
已知圆:及定点,点是圆上的动点,点在上,点在上,且满足=2,
·=. (1)若,求点的轨迹的方程;
(2)若动圆和(1)中所求轨迹相交于不同两点,是否存在一组正实数,使得直线垂直平分线段,若存在,求出这组正实数;若不存在,说明理由.
21.(本小题满分14分)
已知函数的图象过点,且在内单调递减,在上单调递增
(1)求的解析式;
(2)若对于任意的,不等式恒成立,试问这样的是否存在.若存在,请求出的范围,若不存在,说明理由;
新津中学高三数学(文)2月月考试题
一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
C
A
B
C
B
C
B
D
选择题参考答案:
1.解:,选B.
2.解:由对数函数的定义域可得到:
即选C
3. 当;
当,共3个零点,选C
4.,由,,化简可以得到公差,选A
5. 由,则,选B
6.易知圆的直径所在直线符合题意,由圆心,直线的斜率,则根据点斜式方程为;,选C
7.由椭圆的定义可知:,则=16-5=11
选B
8.从三视图中可以看出该几何体是半球体,则表面积,选C
9. 由,则,则,故,选B
10.本题为线性规划和几何概型的综合题,由条件可得到:
,以为横纵坐标作出满足条件的平面区域;
而总面积是由决定的正方形区域
面积之比为,选D
二、填空题:本大题查基本知识和基本运算,体现选择性.共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.
11.
12.
13. ,
14.
15.
填空题参考答案:
11. ;本题考察的对立性
12.由统计知识,该组数据的平均值点,代入方程得到
13.根据框图知识可得到点符合的特征为,由;又因为2010之前的奇数共有1005个,则输出的组数为1005组
14.设半径为,根据平面几何知识(切割线定理)
有,
代入数值可得
15.将曲线化简;得到,作出图像可观察到
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知坐标平面上三点,,.
(1)若(O为原点),求向量与夹角的大小;
解:(1)∵,
,
∴, …………… 2分
∴. …………… 4分
又,,设与的夹角为,则:
,
∴与的夹角为或. ………… 7分
(2)若,求的值.
解 :,
, ……… 9分
由,∴,
可得,① ………… 11分
∴,∴,
…………12分
17.(本小题满分12分)
甲、乙两人参加普法知识竞赛,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙两人依次各抽一题。
① 甲抽到选择题,乙抽到判断题的概率是多少?
解:(1)记 “甲抽到选择题,乙抽到判断题”为事件A, ……2分
甲抽到选择题有6种抽法,乙抽到判断题有4种抽法,
所以事件A的基本事件数为 ………………4分
∴ ……6分
② 甲、乙二人中至少有一人抽到选择题的概率是多少?
解:(2)记“甲、乙两人都抽到判断题”为事件B,
“至少一人抽到选择题”为事件C,
则B含基本事件数为 …………8分
由古典概率公式得 ………10分
由对立事件的性质可得 ……12分
18.(本小题满分14分)
如图5,已知平面,平面,
△为等边三角形,,
为的中点.
(1)求证:平面;
证明:(1) 证:取的中点,连结.
∵为的中点,
∴且.
∵平面,平面,
∴,∴.
又,∴. ………… 4分
∴四边形为平行四边形,则.
∵平面,平面,
∴平面. ………… 7分
(2)求证:平面平面;
证:∵为等边三角形,为的中点,
∴ ∵平面, ………… 9分
平面,∴.
又,故平面.………… 11分
∵,∴平面. ∵平面,
∴平面平面. …………14分
19.(本小题满分14分)
已知数列满足:.
(1)求证:数列为等差数列;
证明:,
=
==. ………………3分
数列为等差数列. ………………4分
(2)求数列的通项公式;
解: 由(1)得,为等差数列,公差为1,
首项为. ………………6分
(. ………………8分
.………9分
(3)令,证明:.
, ………10分
. ………11分
. ………12分
当时,
…………13分
当时,
综上所述:. ………14分
20.(本小题满分14分)
已知圆:及定点,点是圆上的动点,点在上,点在上,且满足
=2, ·=.
(1)若,求点的轨迹的方程;
解:(1)点为的中点,
又,
或点与点重合.∴ …………2分
又
∴点的轨迹是以为焦点的椭圆,
且,
∴的轨迹方程是 …………6分
(2)若动圆和(1)中所求轨迹相交于不同两点,是否存在一组正实数,使得直线垂直平分线段,若存在,求出这组正实数;若不存在,说明理由.
解:不存在这样一组正实数,下面证明: ……7分
由题意,若存在这样的一组正实数,当直线的斜率存在时,
设之为,故直线的方程为:
,设,中点,
则,两式相减得:.…………9分
注意到,
且 ,
则 , ②
又点在直线上,,
代入②式得:.
因为弦的中点在⑴所给椭圆内,故,
这与矛盾,所以所求这组正实数不存在. …………13分
当直线的斜率不存在时,直线的方程为,
则此时,
代入①式得,这与是不同两点矛盾.
综上,所求的这组正实数不存在. ………14分
21.(本小题满分14分)
对于定义域为D的函数,若同时满足下列条件:①在D内单调递增或单调递减;②存在区间[],使在[]上的值域为[];那么把()叫闭函数。
(Ⅰ)求闭函数符合条件②的区间[];
解:(Ⅰ)由题意,在[]上递减,
则
解得…………3分
所以,所求的区间为[-1,1] ………………………4分
(Ⅱ)判断函数是否为闭函数?并说明理由;
解:取则,
即不是上的减函数。…………6分
取
,
即不是上的增函数 …………8分
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。 ---------9分
(Ⅲ)若是闭函数,求实数的取值范围。
解:若是闭函数,则存在区间[],
在区间[]上,函数的值域为[],
即,为方程
的两个实数根,…………10分
即方程有两个不等的实根。
当时,有,
解得 …………12分
当时,有,无解 ……13分
综上所述, -----------14分
同课章节目录
