立体几何中三视图(或直观图)问题的类型与解法 学案
文档属性
| 名称 | 立体几何中三视图(或直观图)问题的类型与解法 学案 |  | |
| 格式 | zip | ||
| 文件大小 | 582.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 11:30:34 | ||
图片预览


文档简介
立体几何中三视图(或直观图)问题的类型与解法
简单几何体三视图(或直观图)问题是近几年高考的热点问题之一,可以这样毫不夸张地说,只要是高考试卷,必然涉及简单几何体三视图(或直观图)的问题。从题型上看,主要是选择题(或填空题),难度系数为中,低档,但有时也可能是高档。纵观近几年的高考,简单几何体三视图(或直观图)问题主要包括:①已知简单几何体的直观图,确定简单几何体的三视图;②已知简单几何体的三视图(或直观图),求简单几何体的表面积(或侧面积或体积);③与简单几何体直观图相关的问题等几种类型。各种类型问题在结构上具有一定的特征,解答方法也有一定的规律可寻,那么在实际解答简单几何体三视图(或直观图)问题时,到底应该如何根据问题的结构特征,选用恰当的方法快捷,准确地作出解答呢?下面通过典型例题的详细解析来回答这个问题。
【典例1】解答下列问题:
1、在一个正方体中,过顶点A的三条棱的中点分别为E,F,G,该正方体截去三棱锥A—EFG后,所得几何体的三视图中,正视图如图所示,相应的侧视图是( )(2021全国高考甲卷)
A B C D
【解析】
【考点】①几何体三视图的定义与性质;②作几何体三视图的基本方法。
【解题思路】根据几何体三视图的性质和作几何体三视图的基本方法,结合问题条件作出该几何体的侧视图就可得出选项。
【详细解答】由所得几何体的正视图可知,原正方体截去的左后下的一个三棱锥,该几何体侧视图是截去一个实线的三角形,应该是D,D正确,选D。
2、以图①为正视图,在图②③④⑤中选两个分部作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可)(2021全国高考乙卷)
【解析】
【考点】①简单几何体三视图定义与性质;②三棱锥定义与性质。
【解题思路】根据解答几何体三视图和三棱锥的性质,就可得到以图①为正视图的三棱锥的侧视图和俯视图。
【详细解答】三棱锥正视图的长为2,高为1,侧视图的高为1,可选图②或图③,俯视图的长与正视图的长相等,俯视图的长为2,可选图④或图⑤,当图②为侧视图时,只能选图⑤作为俯视图,当图③为侧视图时,只能选图④作为俯视图,以图①为正视图的三棱锥的侧视图和俯视图的编号依次是②⑤或③④。
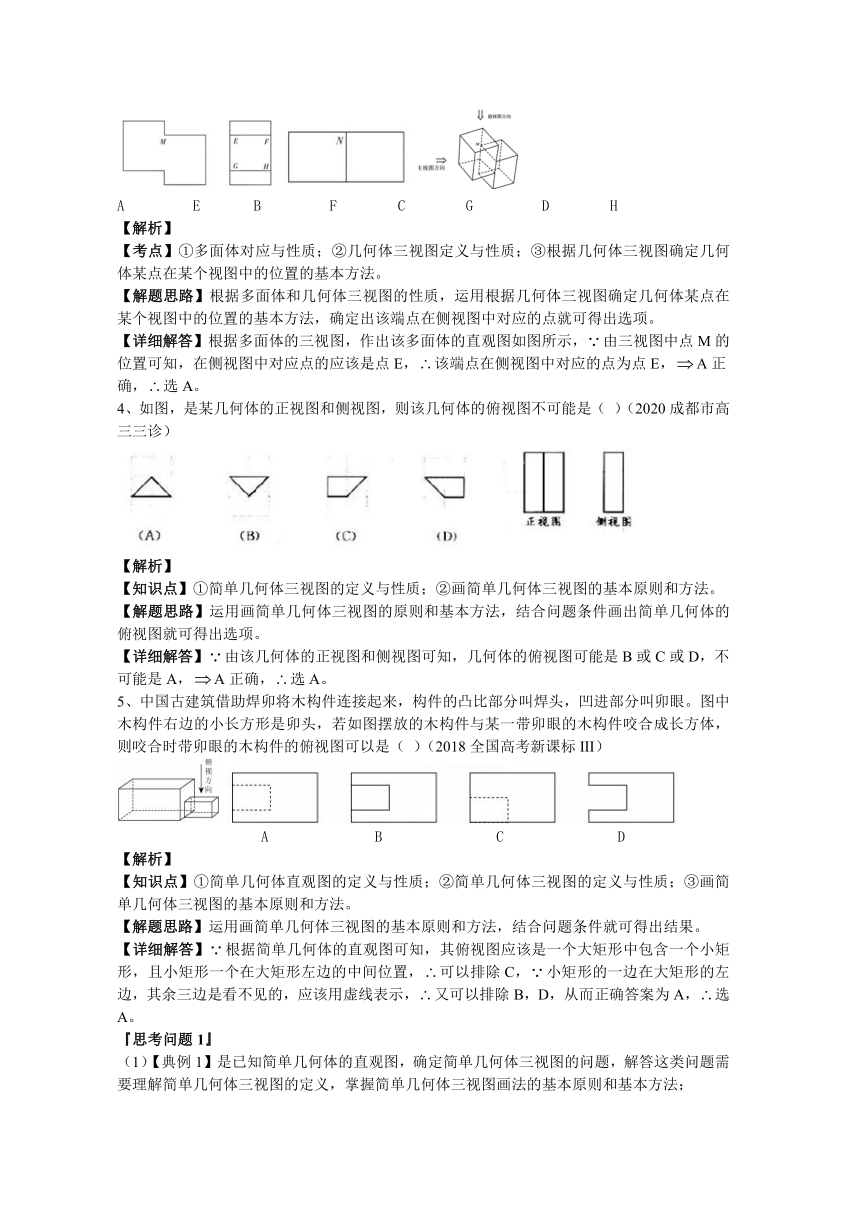
3、如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应点为M,在俯视图中对应点为N,则该端点在侧视图中对应的点为()(2020全国高考新课标II)
A E B F C G D H
【解析】
【考点】①多面体对应与性质;②几何体三视图定义与性质;③根据几何体三视图确定几何体某点在某个视图中的位置的基本方法。
【解题思路】根据多面体和几何体三视图的性质,运用根据几何体三视图确定几何体某点在某个视图中的位置的基本方法,确定出该端点在侧视图中对应的点就可得出选项。
【详细解答】根据多面体的三视图,作出该多面体的直观图如图所示,由三视图中点M的位置可知,在侧视图中对应点的应该是点E,该端点在侧视图中对应的点为点E,A正确,选A。
4、如图,是某几何体的正视图和侧视图,则该几何体的俯视图不可能是( )(2020成都市高三三诊)
【解析】
【知识点】①简单几何体三视图的定义与性质;②画简单几何体三视图的基本原则和方法。
【解题思路】运用画简单几何体三视图的原则和基本方法,结合问题条件画出简单几何体的俯视图就可得出选项。
【详细解答】由该几何体的正视图和侧视图可知,几何体的俯视图可能是B或C或D,不可能是A,A正确,选A。
5、中国古建筑借助焊卯将木构件连接起来,构件的凸比部分叫焊头,凹进部分叫卯眼。图中木构件右边的小长方形是卯头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )(2018全国高考新课标III)
A B C D
【解析】
【知识点】①简单几何体直观图的定义与性质;②简单几何体三视图的定义与性质;③画简单几何体三视图的基本原则和方法。
【解题思路】运用画简单几何体三视图的基本原则和方法,结合问题条件就可得出结果。
【详细解答】根据简单几何体的直观图可知,其俯视图应该是一个大矩形中包含一个小矩形,且小矩形一个在大矩形左边的中间位置,可以排除C,小矩形的一边在大矩形的左边,其余三边是看不见的,应该用虚线表示,又可以排除B,D,从而正确答案为A,选A。
『思考问题1』
(1)【典例1】是已知简单几何体的直观图,确定简单几何体三视图的问题,解答这类问题需要理解简单几何体三视图的定义,掌握简单几何体三视图画法的基本原则和基本方法;
(2)与几何体三视图相关问题主要包括:①已知简单几何体,识别简单几何体的三视图;②已知简单几何体的三视图,判断简单几何体的形状;③已知简单几何体中的两个视图,确定简单几何体第三个视图;
(3)由简单几何体的直观图,确定简单几何体三视图时,应该注意正(主)视图,侧(左)视图和俯视图的观察方向(看到的部分用实线,重叠的线只画一条,不能看到的部分用虚线);
(4)由简单几何体的三视图确定简单几何体的形状,需要熟悉柱,锥,台,球的三视图,注意三视图的形成原理,结合空间想象将三视图还原为简单几何体的直观图;
(5)由简单几何体的部分视图确定简单几何体其余视图,应该先根据已知的一部分视图,推测简单几何体直观图的可能形式,然后再找其剩余部分视图的可能形式,作为选择题可把选项逐项代入,看是否与已知的视图符合。
【典例2】解答下列问题:
1、已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )(2021
全国高考新高考I)
A 2 B 2 C 4 D 4
【解析】
【考点】①简单几何体侧面展开图定义与性质;②圆锥定义与性质。
【解题思路】根据简单几何体展开图和圆锥的性质,结合问题条件求出该圆锥母线的长就可得出选项。
【详细解答】设圆锥的母线长为l,圆锥的底面半径为,圆锥底面的周长为2,圆锥侧面展开图为一个半圆,侧面展开图的半周长为l,l=2,l=2,
B正确,选B。
2、正四棱台的上,下底面的边长分别为2,4,侧棱长为2,则其体积为( )(2021全国高考新高考II)
A 20+12 B 28 C D
【解析】
【考点】①正方形定义与性质;②正四棱台定义与性质;③求正四棱台体积的基本方法。
【解题思路】根据正方形和正四棱台的性质,运用求正四棱台体积的基本方法求出正四棱台的体积,就可得出选项。
【详细解答】如图,连接AC,BD相交于点O,连接, 相交于点,连接O,
===,AO=AC==2, O= = =,正四棱台上底面面积==4,下底面面积==16,正四棱台的体积V= O(++)=(4+16
+)=,D正确,选D。
3、如图,是某几何体的三视图,若三视图中的圆的半径为2,则该几何体的表面积为( )(2021成都市高三零诊)
A 14 B 16 C 18 D 20
【解析】
【考点】①球的定义与性质;②几何体三视图的定义与性质;③根据几何体三视图画几何体直观图的基本方法;④求表面积的计算公式与计算方法。
【解题思路】根据球的性质和由几何体三视图画几何体直观图的基本方法,结合问题条件确定几何体的直观图,利用球表面积的计算公式通过运算就可得出选项。
【详细解答】根据该几何体的三视图可知,几何体是一个球挖去四分之一后剩下的部分,球的半径为2,该几何体的表面积为4-+6=16-4+6=18,C正确,选C。
4、某几何体的三视图如图所示,已知网格纸上的小正方形边长为1,则该几何体的表面积为( )(2021成都市高三三诊)
A (20+8) B (20+4) C (24+8) D (24+4)
【解析】
【考点】①几何体三视图的定义与性质;②已知几何体三视图,确定几何体直观图的基本方法;③圆柱,圆锥的定义与性质;④求圆柱,圆锥表面积的基本方法。
【解题思路】根据几何体三视图的性质和已知几何体三视图确定几何体直观图的基本方法,结合问题条件确定出几何体的直观图,运用圆柱,圆锥的性质和求圆柱,圆锥表面积的基本方法求出几何体的表面积就可得出选项。
【详细解答】由几何体的三视图可知,几何体是一个圆柱和圆锥的组合体,几何体的表面积=4+44+24= (20+8),A正确,选A。
5、如图为某几何体的三视图,则该几何体的表面积是( )(2020全国高考新课标III)
A 6+4 B 4+4 C 6+2 D 4+2
【解析】
【知识点】①简单几何体三视图的定义与性质;②根据简单几何体三视图确定简单几何体直观图的基本方法;③求简单几何体表面积的基本方法。
【解题思路】根据简单几何体三视图,确定简单几何体的直观图,结合问题条件运用求简单几何体表面积的基本方法通过运算求出简单几何体的表面积就可得出选项。
【详细解答】由简单几何体的三视图可知,简单几何体是一个如图所示的三棱锥,=322+22=6+2,C正确,选C。
『思考问题2』
(1)【典例2】是已知简单几何体的三视图,求简单几何体的体积(或表面积或侧面积)的问题,解决这类问题需要理解简单几何体体积,表面积,侧面积的定义,掌握各种简单几何体体积,表面积,侧面积的计算公式和方法;
(2)已知简单几何体的三视图,求该简单几何体的体积,表面积,侧面积的基本方法是:①根据简单几何体的三视图还原简单几何体的直观图;②求出各个面的面积(或底面面积和高);③求各个面积求和(或运用公式求出体积或求出各个侧面面积的和);
(3)以三视图为载体求简单几何体的体积,表面积,侧面积问题的关键是对给出的三视图进行恰当的分析还原简单几何体的直观图,确定几何体是什么几何体;根据三视图还原简单几何体直观图时要注意三视图画法的基本原则:①长对 ;②高平 ;③宽 ;三视图中的实,虚线实际上是原几何体中的可视线与被遮挡的线,注意想象简单几何体原形,进行三视图还原,准确画出简单几何体的直观图是解决该类问题的关键;还原后的简单几何体应该是比较熟悉的柱,锥,台,球或其简单的组合体。
(4)求解简单几何体的体积,表面积,侧面积综合问题的基本方法是:①根据图形分辨清楚简单几何体是柱体,锥体还是台体;②求出公式中的基本量(1》若是体积涉及到底面积和高,2》若是表面积涉及到各个面的面积,3》若是侧面积涉及到各个侧面面积);③运用公式求出结果;
(5)求不规则简单几何体的体积,表面积,侧面积时,一般是将简单几何体分割成基本的柱,锥,台,分别求出各基本几何体的体积,表面积,侧面积再求和;
(6)解答表面积,体积,侧面积最值问题的基本方法是函数法,通过函数的性质求解。
【典例3】解答下列问题:
1、一几何体的三视图如图所示,则该几何体的直观图是( )
【解析】
【知识点】①简单几何体三视图的定义与性质;②根据简单几何体三视图确定简单几何体直观图的基本方法。
【解题思路】运用简单几何体的三视图,结合问题条件,就可确定简单几何体的直观图。
【详细解答】由主视图和侧视图可知,简单几何体是一个组合体,根据俯视图知道组合体上半部分是一个圆台,下半部分是一个圆柱,D正确,选D。
2、学生到工厂劳动实践,利用3D打印技术制作模型如图,该模型为长方体ABCD—挖去四棱锥O—EFGH后所得几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6cm,A=4cm,3D打印所用原料密度为0.9g/cm,不考虑打印损耗,制作该模型所需原料的质量为 ;
【解析】
【知识点】①简单几何体直观图的定义与性质;②根据简单几何体直观图求简单几何体体积的基本方法。
【解题思路】运用简单几何体的直观图,结合问题条件,求出简单几何体的体积,从而求出制作该模型所需原料的质量。
【详细解答】=664=144(cm),=643=12(cm),制作模型的体积=144-12=132(cm),制作该模型所需原料的质量=0.9132=118.8(g)。
3、有一块多边形的菜地,它的水平放置的平 y
面图形的斜二测直观图是直角梯形(如图所示),
,AB=AD=1,DC⊥BC,则这块菜 A D
地的面积为 。 B(O) C x
【解析】
【知识点】①斜二侧画法的定义与性质;②斜而侧法的基本原理和基本方法。
【解题思路】运用斜二侧画法的定义与性质,结合问题条件,确定多边形在直角坐标系中的图形,根据图像通过运算就可求出结果。
【详细解答】由多边形的直观图作出多边形在平面直角坐标系 y
中的图形如图所示,在直观图中过A作AEBC 于点E,
AB=1, AE=BE=,BC=BE+EC=BE+AD=+1,
直角梯形ABCD在直角坐标系中也是直角梯形,且
=1,=2,=+1,这块菜地的面积为: O x
=(1+)2=+1。
『思考问题3』
(1)【典例3】是与简单几何体直观图相关的问题,解答这类问题需要理解简单几何体直观图的定义,掌握简单几何体直观图的画法;
(2)简单几何体直观图的画法—斜二测画法:①画简单几何体的底面:在已知图形中取两条互相垂直的直线分别为X轴和Y轴,两轴的交点为原点,具体画图时使(或),已知图形中与X轴平行的线段在直观图图中长度保持不变,平行Y轴的线段长度变为原来的一半;②画空间几何体的高:在已知图形中过点O作Z轴垂直于XOY平面,在直观图中对应的也要垂直于平面,已知图形中平行于Z轴的线段,在直观图中也要平行轴且长度不变。
(4)简单几何体直观图中的“三变与三不变”:①“三变”是指直观图中坐标轴的夹角要改变,平行于Y轴的线段的长度要改变,直观图与原图相比也要改变;②“三不变”是指平行性不变,与X轴、Z轴平行的线段的平行性不变,相对位置不变。
简单几何体三视图(或直观图)问题是近几年高考的热点问题之一,可以这样毫不夸张地说,只要是高考试卷,必然涉及简单几何体三视图(或直观图)的问题。从题型上看,主要是选择题(或填空题),难度系数为中,低档,但有时也可能是高档。纵观近几年的高考,简单几何体三视图(或直观图)问题主要包括:①已知简单几何体的直观图,确定简单几何体的三视图;②已知简单几何体的三视图(或直观图),求简单几何体的表面积(或侧面积或体积);③与简单几何体直观图相关的问题等几种类型。各种类型问题在结构上具有一定的特征,解答方法也有一定的规律可寻,那么在实际解答简单几何体三视图(或直观图)问题时,到底应该如何根据问题的结构特征,选用恰当的方法快捷,准确地作出解答呢?下面通过典型例题的详细解析来回答这个问题。
【典例1】解答下列问题:
1、在一个正方体中,过顶点A的三条棱的中点分别为E,F,G,该正方体截去三棱锥A—EFG后,所得几何体的三视图中,正视图如图所示,相应的侧视图是( )(2021全国高考甲卷)
A B C D
【解析】
【考点】①几何体三视图的定义与性质;②作几何体三视图的基本方法。
【解题思路】根据几何体三视图的性质和作几何体三视图的基本方法,结合问题条件作出该几何体的侧视图就可得出选项。
【详细解答】由所得几何体的正视图可知,原正方体截去的左后下的一个三棱锥,该几何体侧视图是截去一个实线的三角形,应该是D,D正确,选D。
2、以图①为正视图,在图②③④⑤中选两个分部作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可)(2021全国高考乙卷)
【解析】
【考点】①简单几何体三视图定义与性质;②三棱锥定义与性质。
【解题思路】根据解答几何体三视图和三棱锥的性质,就可得到以图①为正视图的三棱锥的侧视图和俯视图。
【详细解答】三棱锥正视图的长为2,高为1,侧视图的高为1,可选图②或图③,俯视图的长与正视图的长相等,俯视图的长为2,可选图④或图⑤,当图②为侧视图时,只能选图⑤作为俯视图,当图③为侧视图时,只能选图④作为俯视图,以图①为正视图的三棱锥的侧视图和俯视图的编号依次是②⑤或③④。
3、如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应点为M,在俯视图中对应点为N,则该端点在侧视图中对应的点为()(2020全国高考新课标II)
A E B F C G D H
【解析】
【考点】①多面体对应与性质;②几何体三视图定义与性质;③根据几何体三视图确定几何体某点在某个视图中的位置的基本方法。
【解题思路】根据多面体和几何体三视图的性质,运用根据几何体三视图确定几何体某点在某个视图中的位置的基本方法,确定出该端点在侧视图中对应的点就可得出选项。
【详细解答】根据多面体的三视图,作出该多面体的直观图如图所示,由三视图中点M的位置可知,在侧视图中对应点的应该是点E,该端点在侧视图中对应的点为点E,A正确,选A。
4、如图,是某几何体的正视图和侧视图,则该几何体的俯视图不可能是( )(2020成都市高三三诊)
【解析】
【知识点】①简单几何体三视图的定义与性质;②画简单几何体三视图的基本原则和方法。
【解题思路】运用画简单几何体三视图的原则和基本方法,结合问题条件画出简单几何体的俯视图就可得出选项。
【详细解答】由该几何体的正视图和侧视图可知,几何体的俯视图可能是B或C或D,不可能是A,A正确,选A。
5、中国古建筑借助焊卯将木构件连接起来,构件的凸比部分叫焊头,凹进部分叫卯眼。图中木构件右边的小长方形是卯头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )(2018全国高考新课标III)
A B C D
【解析】
【知识点】①简单几何体直观图的定义与性质;②简单几何体三视图的定义与性质;③画简单几何体三视图的基本原则和方法。
【解题思路】运用画简单几何体三视图的基本原则和方法,结合问题条件就可得出结果。
【详细解答】根据简单几何体的直观图可知,其俯视图应该是一个大矩形中包含一个小矩形,且小矩形一个在大矩形左边的中间位置,可以排除C,小矩形的一边在大矩形的左边,其余三边是看不见的,应该用虚线表示,又可以排除B,D,从而正确答案为A,选A。
『思考问题1』
(1)【典例1】是已知简单几何体的直观图,确定简单几何体三视图的问题,解答这类问题需要理解简单几何体三视图的定义,掌握简单几何体三视图画法的基本原则和基本方法;
(2)与几何体三视图相关问题主要包括:①已知简单几何体,识别简单几何体的三视图;②已知简单几何体的三视图,判断简单几何体的形状;③已知简单几何体中的两个视图,确定简单几何体第三个视图;
(3)由简单几何体的直观图,确定简单几何体三视图时,应该注意正(主)视图,侧(左)视图和俯视图的观察方向(看到的部分用实线,重叠的线只画一条,不能看到的部分用虚线);
(4)由简单几何体的三视图确定简单几何体的形状,需要熟悉柱,锥,台,球的三视图,注意三视图的形成原理,结合空间想象将三视图还原为简单几何体的直观图;
(5)由简单几何体的部分视图确定简单几何体其余视图,应该先根据已知的一部分视图,推测简单几何体直观图的可能形式,然后再找其剩余部分视图的可能形式,作为选择题可把选项逐项代入,看是否与已知的视图符合。
【典例2】解答下列问题:
1、已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )(2021
全国高考新高考I)
A 2 B 2 C 4 D 4
【解析】
【考点】①简单几何体侧面展开图定义与性质;②圆锥定义与性质。
【解题思路】根据简单几何体展开图和圆锥的性质,结合问题条件求出该圆锥母线的长就可得出选项。
【详细解答】设圆锥的母线长为l,圆锥的底面半径为,圆锥底面的周长为2,圆锥侧面展开图为一个半圆,侧面展开图的半周长为l,l=2,l=2,
B正确,选B。
2、正四棱台的上,下底面的边长分别为2,4,侧棱长为2,则其体积为( )(2021全国高考新高考II)
A 20+12 B 28 C D
【解析】
【考点】①正方形定义与性质;②正四棱台定义与性质;③求正四棱台体积的基本方法。
【解题思路】根据正方形和正四棱台的性质,运用求正四棱台体积的基本方法求出正四棱台的体积,就可得出选项。
【详细解答】如图,连接AC,BD相交于点O,连接, 相交于点,连接O,
===,AO=AC==2, O= = =,正四棱台上底面面积==4,下底面面积==16,正四棱台的体积V= O(++)=(4+16
+)=,D正确,选D。
3、如图,是某几何体的三视图,若三视图中的圆的半径为2,则该几何体的表面积为( )(2021成都市高三零诊)
A 14 B 16 C 18 D 20
【解析】
【考点】①球的定义与性质;②几何体三视图的定义与性质;③根据几何体三视图画几何体直观图的基本方法;④求表面积的计算公式与计算方法。
【解题思路】根据球的性质和由几何体三视图画几何体直观图的基本方法,结合问题条件确定几何体的直观图,利用球表面积的计算公式通过运算就可得出选项。
【详细解答】根据该几何体的三视图可知,几何体是一个球挖去四分之一后剩下的部分,球的半径为2,该几何体的表面积为4-+6=16-4+6=18,C正确,选C。
4、某几何体的三视图如图所示,已知网格纸上的小正方形边长为1,则该几何体的表面积为( )(2021成都市高三三诊)
A (20+8) B (20+4) C (24+8) D (24+4)
【解析】
【考点】①几何体三视图的定义与性质;②已知几何体三视图,确定几何体直观图的基本方法;③圆柱,圆锥的定义与性质;④求圆柱,圆锥表面积的基本方法。
【解题思路】根据几何体三视图的性质和已知几何体三视图确定几何体直观图的基本方法,结合问题条件确定出几何体的直观图,运用圆柱,圆锥的性质和求圆柱,圆锥表面积的基本方法求出几何体的表面积就可得出选项。
【详细解答】由几何体的三视图可知,几何体是一个圆柱和圆锥的组合体,几何体的表面积=4+44+24= (20+8),A正确,选A。
5、如图为某几何体的三视图,则该几何体的表面积是( )(2020全国高考新课标III)
A 6+4 B 4+4 C 6+2 D 4+2
【解析】
【知识点】①简单几何体三视图的定义与性质;②根据简单几何体三视图确定简单几何体直观图的基本方法;③求简单几何体表面积的基本方法。
【解题思路】根据简单几何体三视图,确定简单几何体的直观图,结合问题条件运用求简单几何体表面积的基本方法通过运算求出简单几何体的表面积就可得出选项。
【详细解答】由简单几何体的三视图可知,简单几何体是一个如图所示的三棱锥,=322+22=6+2,C正确,选C。
『思考问题2』
(1)【典例2】是已知简单几何体的三视图,求简单几何体的体积(或表面积或侧面积)的问题,解决这类问题需要理解简单几何体体积,表面积,侧面积的定义,掌握各种简单几何体体积,表面积,侧面积的计算公式和方法;
(2)已知简单几何体的三视图,求该简单几何体的体积,表面积,侧面积的基本方法是:①根据简单几何体的三视图还原简单几何体的直观图;②求出各个面的面积(或底面面积和高);③求各个面积求和(或运用公式求出体积或求出各个侧面面积的和);
(3)以三视图为载体求简单几何体的体积,表面积,侧面积问题的关键是对给出的三视图进行恰当的分析还原简单几何体的直观图,确定几何体是什么几何体;根据三视图还原简单几何体直观图时要注意三视图画法的基本原则:①长对 ;②高平 ;③宽 ;三视图中的实,虚线实际上是原几何体中的可视线与被遮挡的线,注意想象简单几何体原形,进行三视图还原,准确画出简单几何体的直观图是解决该类问题的关键;还原后的简单几何体应该是比较熟悉的柱,锥,台,球或其简单的组合体。
(4)求解简单几何体的体积,表面积,侧面积综合问题的基本方法是:①根据图形分辨清楚简单几何体是柱体,锥体还是台体;②求出公式中的基本量(1》若是体积涉及到底面积和高,2》若是表面积涉及到各个面的面积,3》若是侧面积涉及到各个侧面面积);③运用公式求出结果;
(5)求不规则简单几何体的体积,表面积,侧面积时,一般是将简单几何体分割成基本的柱,锥,台,分别求出各基本几何体的体积,表面积,侧面积再求和;
(6)解答表面积,体积,侧面积最值问题的基本方法是函数法,通过函数的性质求解。
【典例3】解答下列问题:
1、一几何体的三视图如图所示,则该几何体的直观图是( )
【解析】
【知识点】①简单几何体三视图的定义与性质;②根据简单几何体三视图确定简单几何体直观图的基本方法。
【解题思路】运用简单几何体的三视图,结合问题条件,就可确定简单几何体的直观图。
【详细解答】由主视图和侧视图可知,简单几何体是一个组合体,根据俯视图知道组合体上半部分是一个圆台,下半部分是一个圆柱,D正确,选D。
2、学生到工厂劳动实践,利用3D打印技术制作模型如图,该模型为长方体ABCD—挖去四棱锥O—EFGH后所得几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6cm,A=4cm,3D打印所用原料密度为0.9g/cm,不考虑打印损耗,制作该模型所需原料的质量为 ;
【解析】
【知识点】①简单几何体直观图的定义与性质;②根据简单几何体直观图求简单几何体体积的基本方法。
【解题思路】运用简单几何体的直观图,结合问题条件,求出简单几何体的体积,从而求出制作该模型所需原料的质量。
【详细解答】=664=144(cm),=643=12(cm),制作模型的体积=144-12=132(cm),制作该模型所需原料的质量=0.9132=118.8(g)。
3、有一块多边形的菜地,它的水平放置的平 y
面图形的斜二测直观图是直角梯形(如图所示),
,AB=AD=1,DC⊥BC,则这块菜 A D
地的面积为 。 B(O) C x
【解析】
【知识点】①斜二侧画法的定义与性质;②斜而侧法的基本原理和基本方法。
【解题思路】运用斜二侧画法的定义与性质,结合问题条件,确定多边形在直角坐标系中的图形,根据图像通过运算就可求出结果。
【详细解答】由多边形的直观图作出多边形在平面直角坐标系 y
中的图形如图所示,在直观图中过A作AEBC 于点E,
AB=1, AE=BE=,BC=BE+EC=BE+AD=+1,
直角梯形ABCD在直角坐标系中也是直角梯形,且
=1,=2,=+1,这块菜地的面积为: O x
=(1+)2=+1。
『思考问题3』
(1)【典例3】是与简单几何体直观图相关的问题,解答这类问题需要理解简单几何体直观图的定义,掌握简单几何体直观图的画法;
(2)简单几何体直观图的画法—斜二测画法:①画简单几何体的底面:在已知图形中取两条互相垂直的直线分别为X轴和Y轴,两轴的交点为原点,具体画图时使(或),已知图形中与X轴平行的线段在直观图图中长度保持不变,平行Y轴的线段长度变为原来的一半;②画空间几何体的高:在已知图形中过点O作Z轴垂直于XOY平面,在直观图中对应的也要垂直于平面,已知图形中平行于Z轴的线段,在直观图中也要平行轴且长度不变。
(4)简单几何体直观图中的“三变与三不变”:①“三变”是指直观图中坐标轴的夹角要改变,平行于Y轴的线段的长度要改变,直观图与原图相比也要改变;②“三不变”是指平行性不变,与X轴、Z轴平行的线段的平行性不变,相对位置不变。
同课章节目录
