7.2万有引力定律(共20张ppt)
文档属性
| 名称 | 7.2万有引力定律(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-28 13:50:57 | ||
图片预览



文档简介
(共20张PPT)
6.4 生活中的圆周运动
第6章 圆周运动
(1)行星绕太阳运动的轨道十分接近圆,太阳处在圆心;
一、行星与太阳的引力
(2)行星做匀速圆周运动;
(3)所有行星轨道半径 r 的三次方与它公转周期 T 的二次方
的比值都相等,即: 。
行星绕太阳做匀速圆周运动需要的向心力由什么力来提供呢? 这个力的大小和方向分别是?
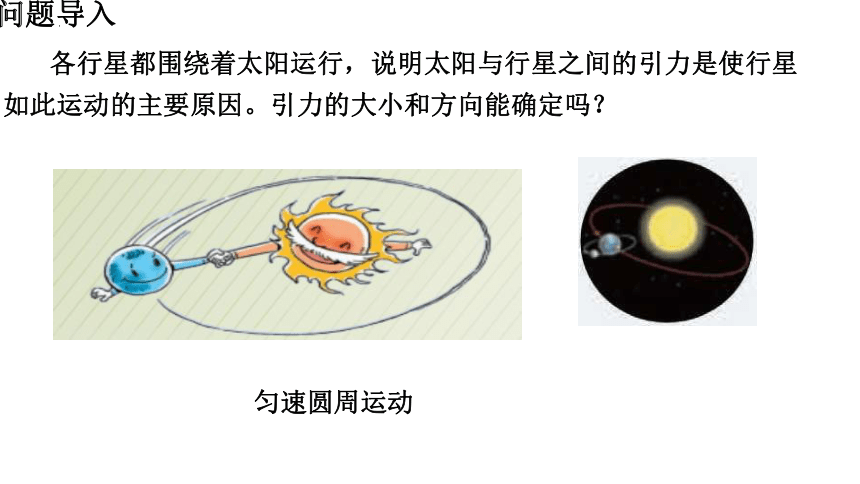
问题导入
各行星都围绕着太阳运行,说明太阳与行星之间的引力是使行星如此运动的主要原因。引力的大小和方向能确定吗?
匀速圆周运动
伽利略
行星的运动是受到了来自太阳的类似于磁力的作用 ,与距离成反比。
行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
在行星的周围有旋转的物质作用在行星上,使得行星绕太阳运动。
开普勒
笛卡尔
胡克
科学的足迹
行星的运动与地面物体的运动遵从不同的规律,是”惯性”自行维持的
开普勒发现行星运动三大定律之后,人们就开始寻找行星这样运动的原因?
牛顿在前人对惯性研究的基础上,他提出
牛顿 (1643—1727)
英国著名的物理学家
使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点的力,这个力应该就是太阳对它的引力
下面,我们根据牛顿运动定律及开普勒行星运动定律来讨论行星与太阳间的引力。
太阳
行星 m
a
行星 m
r
行星绕太阳做匀速圆周运动
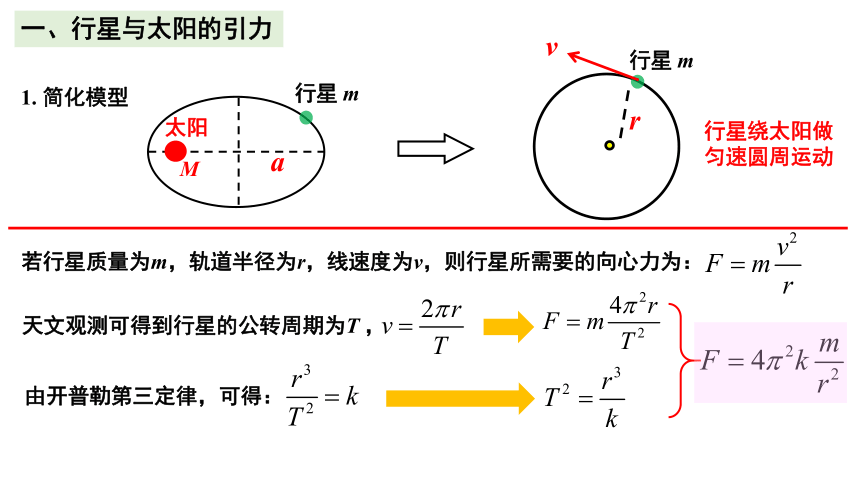
1. 简化模型
一、行星与太阳的引力
若行星质量为m,轨道半径为r,线速度为v,则行星所需要的向心力为:
天文观测可得到行星的公转周期为T ,
由开普勒第三定律,可得:
v
M
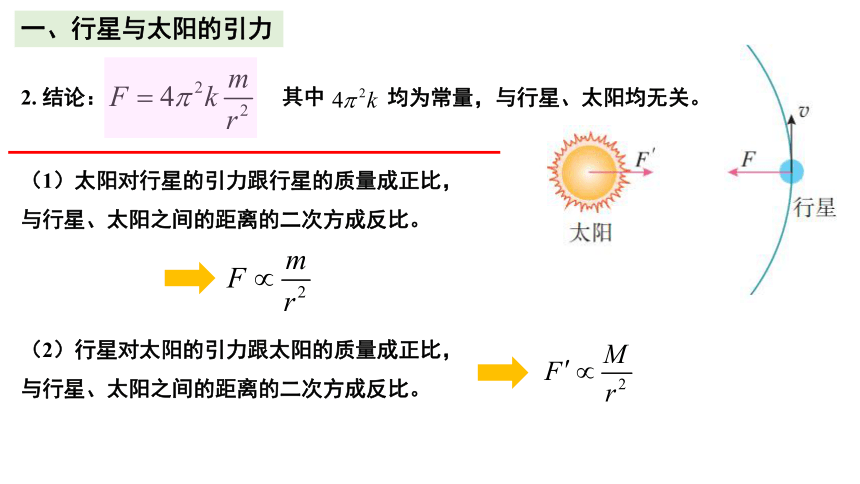
(2)行星对太阳的引力跟太阳的质量成正比,
与行星、太阳之间的距离的二次方成反比。
(1)太阳对行星的引力跟行星的质量成正比,
与行星、太阳之间的距离的二次方成反比。
一、行星与太阳的引力
2. 结论:
其中
均为常量,与行星、太阳均无关。
与太阳、行星的质量成正比,与两者距离的平方成反比;
一、行星与太阳的引力
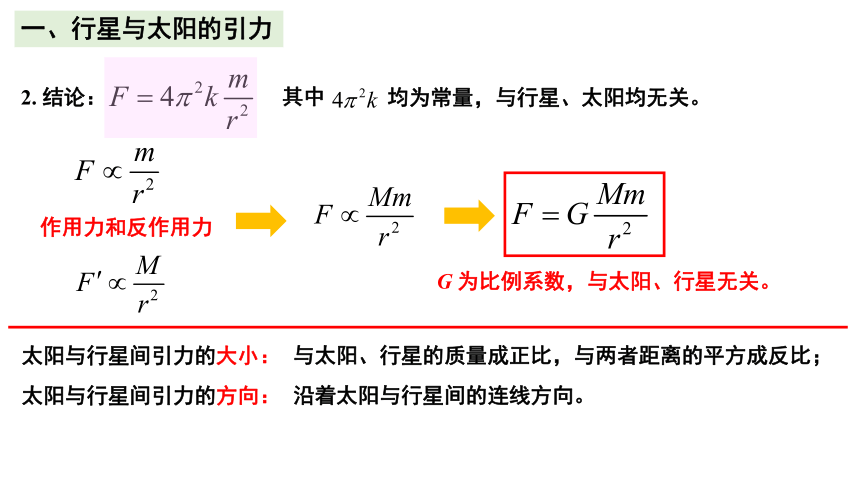
2. 结论:
其中
均为常量,与行星、太阳均无关。
作用力和反作用力
太阳与行星间引力的大小:
G 为比例系数,与太阳、行星无关。
沿着太阳与行星间的连线方向。
太阳与行星间引力的方向:
苹果成熟之后,落到地面上,是不是也是因为地球的吸引呢?
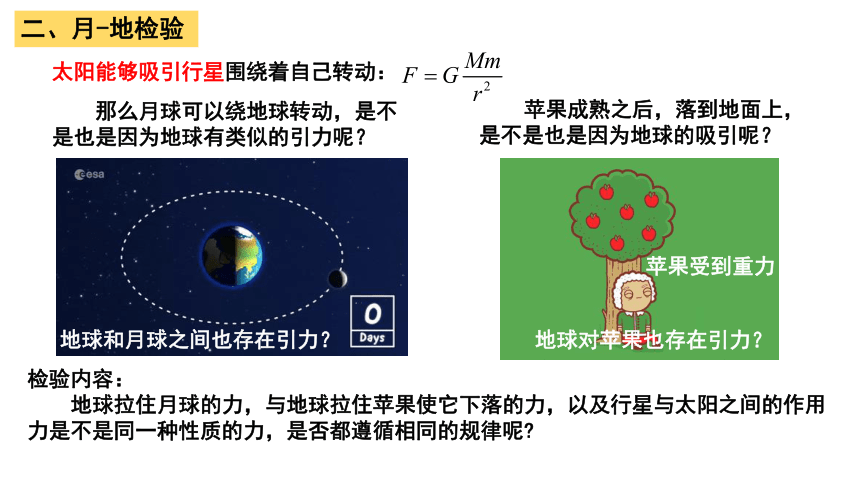
二、月-地检验
检验内容:
地球拉住月球的力,与地球拉住苹果使它下落的力,以及行星与太阳之间的作用力是不是同一种性质的力,是否都遵循相同的规律呢
太阳能够吸引行星围绕着自己转动:
那么月球可以绕地球转动,是不是也是因为地球有类似的引力呢?
地球和月球之间也存在引力?
苹果受到重力
地球对苹果也存在引力?
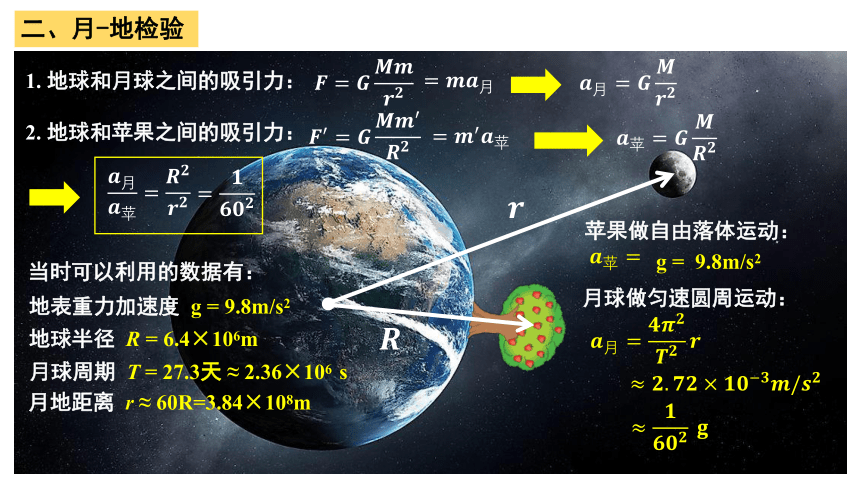
1. 地球和月球之间的吸引力:
二、月-地检验
2. 地球和苹果之间的吸引力:
地球半径 R = 6.4×106m
当时可以利用的数据有:
地表重力加速度 g = 9.8m/s2
月地距离 r ≈ 60R=3.84×108m
月球周期 T = 27.3天 ≈ 2.36×106 s
苹果做自由落体运动:
g = 9.8m/s2
月球做匀速圆周运动:
3. 数据表明:地面物体所受地球的引力,月球所受地球的引力,与太阳行星间的引力,都遵循相同的规律!
如果将思路打开,是否宇宙中任意两个具有质量物体之间都存在这样的引力
二、月-地检验
G 为比例系数,与太阳、行星无关。
万有引力!!!
牛顿的思考
既然太阳与行星间、地球与月球间、地球与物体间都有引力,那么任何两个有质量的物体间是否也都有这样的引力呢?
方向:在两物体的连线上。
三、万有引力定律
r 的物理意义:
(1)对于可以看做质点的物体,r为两个质点之间的距离;
(2)对于质量分布均匀的球体,r为两个球心之间的距离;
(3)质量分布均匀的球体与球外一质点,r为质点到球心的距离。
当r趋近于0时,物体不能视为质点,万有引力公式不再适用,而不是引力F趋于无穷大。
m1
m2
r
自然界中任何两个物体都相互吸引,引力的大小与物体的质量m1和m2的乘积成正比,与它们之间距离r的二次方成反比。
m1和m2表示两个物体的质量,r表示两个球心之间的距离
G是比例系数,叫做引力常量,适用于任何两个物体。
(1)单位:
(2)大小:
(3)引力常量G的测定:卡文迪许扭秤实验
三、万有引力定律
三、万有引力定律
如图,两球间的距离为r0。两球的质量分布均匀,质量分别为m1、m2,半径分别为r1、r2,引力常量为G,则两球间的万有引力大小为
√
练习
万有引力定律
月球绕地球
行星绕太阳
地球表面物体
月球绕地球
同种性质的力
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
1. 人在不同位置受到的万有引力的大小和方向?
将地球视为一个规则的球体
将地球视为一个规则的球体
将人视为一个质点
方向均由人沿半径指向地心。
四、万有引力和重力的关系
O
w
引
引
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
2. 人在不同位置,什么力提供向心力?
引
向
mg
向
向心力由万有引力的一个分力去充当。
按照矢量的平行四边形法则,万有引力还会有另一个分力——就是我们以前学过的重力。
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
3. 人在北极点的受力分析(南极点的情况相同)
引
= 0
向
= mg
引
= 0
向
mg =
引
此时重力加速度 g 最大,
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
4. 人在赤道上的受力分析
引
向
mg
引
向
+ mg
引
此时重力加速度 g 最小。
向
mg =
引
向
从赤道到两极:随着纬度增加,向心力减小,重力mg在增大,重力加速度g增大。
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
5. 若是忽略地球的自转,则不考虑向心力,即物体受到的万有引力总是等于物体的重力。
引
mg
地球自转的角速度:
6.4 生活中的圆周运动
第6章 圆周运动
(1)行星绕太阳运动的轨道十分接近圆,太阳处在圆心;
一、行星与太阳的引力
(2)行星做匀速圆周运动;
(3)所有行星轨道半径 r 的三次方与它公转周期 T 的二次方
的比值都相等,即: 。
行星绕太阳做匀速圆周运动需要的向心力由什么力来提供呢? 这个力的大小和方向分别是?
问题导入
各行星都围绕着太阳运行,说明太阳与行星之间的引力是使行星如此运动的主要原因。引力的大小和方向能确定吗?
匀速圆周运动
伽利略
行星的运动是受到了来自太阳的类似于磁力的作用 ,与距离成反比。
行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
在行星的周围有旋转的物质作用在行星上,使得行星绕太阳运动。
开普勒
笛卡尔
胡克
科学的足迹
行星的运动与地面物体的运动遵从不同的规律,是”惯性”自行维持的
开普勒发现行星运动三大定律之后,人们就开始寻找行星这样运动的原因?
牛顿在前人对惯性研究的基础上,他提出
牛顿 (1643—1727)
英国著名的物理学家
使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点的力,这个力应该就是太阳对它的引力
下面,我们根据牛顿运动定律及开普勒行星运动定律来讨论行星与太阳间的引力。
太阳
行星 m
a
行星 m
r
行星绕太阳做匀速圆周运动
1. 简化模型
一、行星与太阳的引力
若行星质量为m,轨道半径为r,线速度为v,则行星所需要的向心力为:
天文观测可得到行星的公转周期为T ,
由开普勒第三定律,可得:
v
M
(2)行星对太阳的引力跟太阳的质量成正比,
与行星、太阳之间的距离的二次方成反比。
(1)太阳对行星的引力跟行星的质量成正比,
与行星、太阳之间的距离的二次方成反比。
一、行星与太阳的引力
2. 结论:
其中
均为常量,与行星、太阳均无关。
与太阳、行星的质量成正比,与两者距离的平方成反比;
一、行星与太阳的引力
2. 结论:
其中
均为常量,与行星、太阳均无关。
作用力和反作用力
太阳与行星间引力的大小:
G 为比例系数,与太阳、行星无关。
沿着太阳与行星间的连线方向。
太阳与行星间引力的方向:
苹果成熟之后,落到地面上,是不是也是因为地球的吸引呢?
二、月-地检验
检验内容:
地球拉住月球的力,与地球拉住苹果使它下落的力,以及行星与太阳之间的作用力是不是同一种性质的力,是否都遵循相同的规律呢
太阳能够吸引行星围绕着自己转动:
那么月球可以绕地球转动,是不是也是因为地球有类似的引力呢?
地球和月球之间也存在引力?
苹果受到重力
地球对苹果也存在引力?
1. 地球和月球之间的吸引力:
二、月-地检验
2. 地球和苹果之间的吸引力:
地球半径 R = 6.4×106m
当时可以利用的数据有:
地表重力加速度 g = 9.8m/s2
月地距离 r ≈ 60R=3.84×108m
月球周期 T = 27.3天 ≈ 2.36×106 s
苹果做自由落体运动:
g = 9.8m/s2
月球做匀速圆周运动:
3. 数据表明:地面物体所受地球的引力,月球所受地球的引力,与太阳行星间的引力,都遵循相同的规律!
如果将思路打开,是否宇宙中任意两个具有质量物体之间都存在这样的引力
二、月-地检验
G 为比例系数,与太阳、行星无关。
万有引力!!!
牛顿的思考
既然太阳与行星间、地球与月球间、地球与物体间都有引力,那么任何两个有质量的物体间是否也都有这样的引力呢?
方向:在两物体的连线上。
三、万有引力定律
r 的物理意义:
(1)对于可以看做质点的物体,r为两个质点之间的距离;
(2)对于质量分布均匀的球体,r为两个球心之间的距离;
(3)质量分布均匀的球体与球外一质点,r为质点到球心的距离。
当r趋近于0时,物体不能视为质点,万有引力公式不再适用,而不是引力F趋于无穷大。
m1
m2
r
自然界中任何两个物体都相互吸引,引力的大小与物体的质量m1和m2的乘积成正比,与它们之间距离r的二次方成反比。
m1和m2表示两个物体的质量,r表示两个球心之间的距离
G是比例系数,叫做引力常量,适用于任何两个物体。
(1)单位:
(2)大小:
(3)引力常量G的测定:卡文迪许扭秤实验
三、万有引力定律
三、万有引力定律
如图,两球间的距离为r0。两球的质量分布均匀,质量分别为m1、m2,半径分别为r1、r2,引力常量为G,则两球间的万有引力大小为
√
练习
万有引力定律
月球绕地球
行星绕太阳
地球表面物体
月球绕地球
同种性质的力
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
1. 人在不同位置受到的万有引力的大小和方向?
将地球视为一个规则的球体
将地球视为一个规则的球体
将人视为一个质点
方向均由人沿半径指向地心。
四、万有引力和重力的关系
O
w
引
引
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
2. 人在不同位置,什么力提供向心力?
引
向
mg
向
向心力由万有引力的一个分力去充当。
按照矢量的平行四边形法则,万有引力还会有另一个分力——就是我们以前学过的重力。
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
3. 人在北极点的受力分析(南极点的情况相同)
引
= 0
向
= mg
引
= 0
向
mg =
引
此时重力加速度 g 最大,
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
4. 人在赤道上的受力分析
引
向
mg
引
向
+ mg
引
此时重力加速度 g 最小。
向
mg =
引
向
从赤道到两极:随着纬度增加,向心力减小,重力mg在增大,重力加速度g增大。
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
5. 若是忽略地球的自转,则不考虑向心力,即物体受到的万有引力总是等于物体的重力。
引
mg
地球自转的角速度:
