苏教版五年级数学下册七 解决问题的策略《3.解决问题的策略----转化》教学设计
文档属性
| 名称 | 苏教版五年级数学下册七 解决问题的策略《3.解决问题的策略----转化》教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 25.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-28 19:51:06 | ||
图片预览

文档简介
解决问题的策略----转化
教学内容:
苏教版第10册第105—106页的例1、“练一练”和练习十六的第1—3题。
教学目标:
1.学生能体验转化的价值,掌握一些具体的转化方法,进一步积累转化的经验,增强自觉运用转化策略解决问题的意识。
2.学生能体验数学文化独特的美,激发学生热爱数学的美好情感。
教学重难点
学生能体验转化的价值,掌握一些具体的转化方法,进一步积累转化的经验,增强自觉运用转化策略解决问题的意识。
教学过程:
一、故事导入,做好铺垫
1.导入:(出示曹冲称象图)同学们,你们知道这幅图讲了一个什么故事吗?谁能把故事简要地说一说。
师:面对“大象”这个庞然大物,7岁的曹冲是怎样巧妙称出它的重量的 曹冲聪明在哪里呢
生:曹冲化大为小,将称大象转化为称小石头。
生:曹冲用转化的方法称出了大象的重量。
……
师:大象太大了,当时没有工具能直接称出它的重量,曹冲想到把它变成称“小石头”的重量,从而知道大象的重量,非常有新意,非常了不起,我想我们同学在今天以及以后的学习中也会像曹冲一样,遇到问题多动脑,多思考,一定能想出解决问题的好办法。下面我们就带着思考来看一组图形。
二、初步感知,体会价值
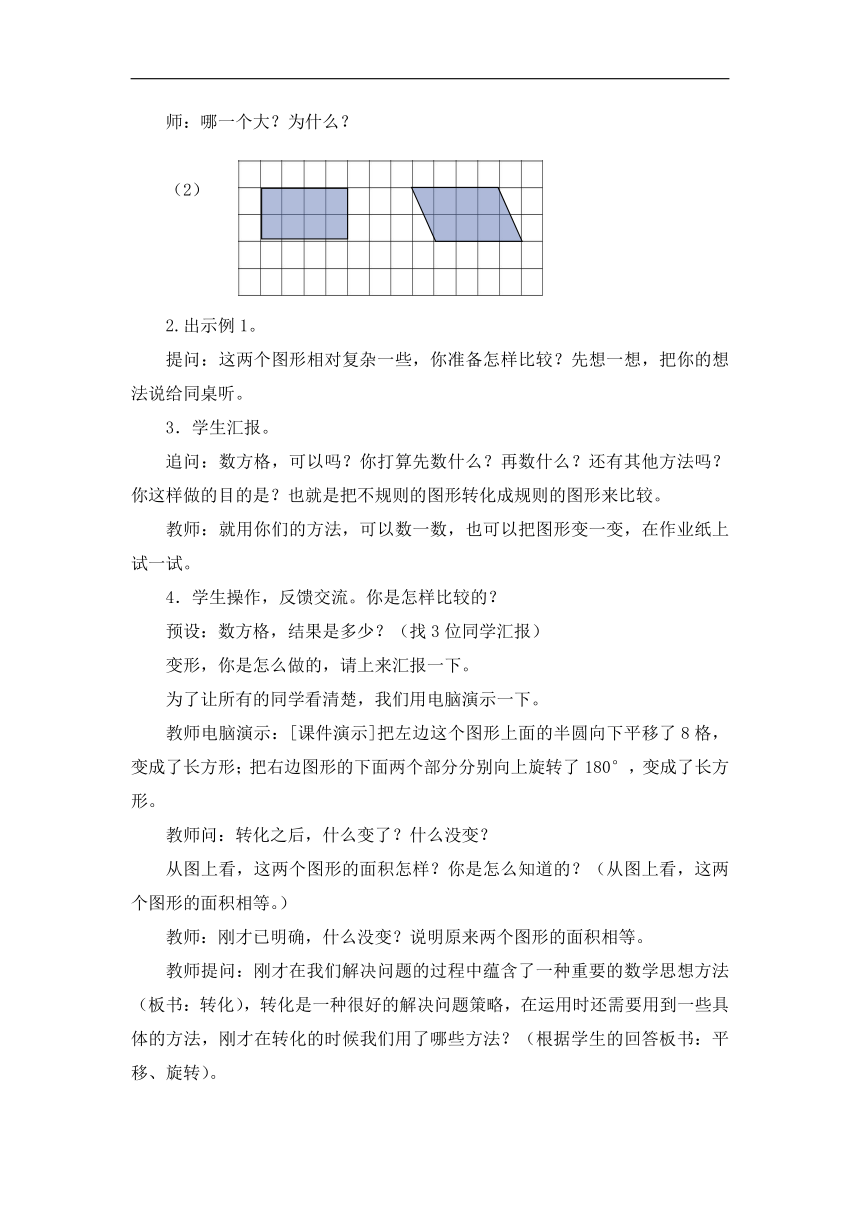
1.请学生仔细观察,下面两个图形,哪个面积大一些?
(1)
师:哪一个大?为什么?
(2)
2.出示例1。
提问:这两个图形相对复杂一些,你准备怎样比较?先想一想,把你的想法说给同桌听。
学生汇报。
追问:数方格,可以吗?你打算先数什么?再数什么?还有其他方法吗?你这样做的目的是?也就是把不规则的图形转化成规则的图形来比较。
教师:就用你们的方法,可以数一数,也可以把图形变一变,在作业纸上试一试。
学生操作,反馈交流。你是怎样比较的?
预设:数方格,结果是多少?(找3位同学汇报)
变形,你是怎么做的,请上来汇报一下。
为了让所有的同学看清楚,我们用电脑演示一下。
教师电脑演示:[课件演示]把左边这个图形上面的半圆向下平移了8格,变成了长方形;把右边图形的下面两个部分分别向上旋转了180°,变成了长方形。
教师问:转化之后,什么变了?什么没变?
从图上看,这两个图形的面积怎样?你是怎么知道的?(从图上看,这两个图形的面积相等。)
教师:刚才已明确,什么没变?说明原来两个图形的面积相等。
教师提问:刚才在我们解决问题的过程中蕴含了一种重要的数学思想方法(板书:转化),转化是一种很好的解决问题策略,在运用时还需要用到一些具体的方法,刚才在转化的时候我们用了哪些方法?(根据学生的回答板书:平移、旋转)。
教师提问:[课件演示:回到原来的两个图]刚才我们有同学用数方格的方法来比较,结果准确吗?
说明不“转化”,解决这个问题的过程挺复杂的。回顾刚才解决问题的过程,你有什么体会?
预设:(1)为什么刚开始我们看不出这两个图形的面积相等,现在一下子就能看出来呢?(预设:运用“转化”策略,可以让复杂的解决问题过程变得简单。(板书: 复杂 转化 简单 )
(2)观察并回顾刚才的转化过程,什么变了?什么没有变?
三、丰富外延,探寻本质
1.对于转化,其实我们一点都不陌生,在以前的学习过程中,早就运用转化的策略解决了许多问题。比如,我们在不会算平行四边形的面积时,需要推导面积公式时,是怎么做的?(课件演示)现在请你回想一下,我们曾经运用转化的策略还解决过哪些问题?
2.讨论:你们有没有发现,刚才我们举得这些例子,都不约而同地用到了什么策略?都是在什么情况下用了转化的策略?(化未知为已知;化复杂为简单等等)(板书:未知 已知)
3.追问:如果以后你再遇到一个复杂或陌生的问题时,可以怎么想?
下面我们一起去闯关好吗?
四、实践运用,探索方法
1.第一关:小试牛刀(练习十六第1题)
(1)指名读题: 右边图形的周长该怎样计算简便呢?和你的同桌交流一下。
(2)交流反馈:你为什么要转化?怎样转化?课件演示。转化前后什么不能变?(板书 :周长不变)
2.第二关:乘胜追击(练习十六2)
(1)学生独立解答,交流。第一个:你是怎么想的?还可以?这样就更直观的看出涂色部分了。第二个:你是怎么想的?还可以?这两个图形转化前后什么不能变?
(2)重点交流第三个。你是怎么想的?课件辅助为什么十六分之九是错的?让学生上台动手转一转,观察到涂色部分比十六分之九要大些。课件再对比十六分之九与十六分之十。还可以怎样想?课件演示旋转拼摆。还有不同想法吗?思考空白部分。
3.第三关:大显身手(练一练与练习十六3变形拓展)
指名读题。
(1)师:看他们是怎么设计的 这两种设计小路面积相等吗?为什么?那剩下草坪面积也相等。
(2)师:如果长方形长是45米,宽是27米,剩下草坪面积是多少?在练习纸上写一写。集体交流。
(3)如果要想草坪的面积不变,这两条小路还可以怎样设计?为什么?也就是平行于两条长、宽之间的任意一条。小路的设计可以非常的丰富,但无论哪种设计,剩下草坪的面积都是一样的,都可以用这一个算式来表示。
(4)拓展:再增加几条小路,如何求草坪的面积?
五、全课小结
今天这节课我们一起学习了解决问题的策略是转化。你为什么要转化?怎么转化?转化的依据是什么?
教学内容:
苏教版第10册第105—106页的例1、“练一练”和练习十六的第1—3题。
教学目标:
1.学生能体验转化的价值,掌握一些具体的转化方法,进一步积累转化的经验,增强自觉运用转化策略解决问题的意识。
2.学生能体验数学文化独特的美,激发学生热爱数学的美好情感。
教学重难点
学生能体验转化的价值,掌握一些具体的转化方法,进一步积累转化的经验,增强自觉运用转化策略解决问题的意识。
教学过程:
一、故事导入,做好铺垫
1.导入:(出示曹冲称象图)同学们,你们知道这幅图讲了一个什么故事吗?谁能把故事简要地说一说。
师:面对“大象”这个庞然大物,7岁的曹冲是怎样巧妙称出它的重量的 曹冲聪明在哪里呢
生:曹冲化大为小,将称大象转化为称小石头。
生:曹冲用转化的方法称出了大象的重量。
……
师:大象太大了,当时没有工具能直接称出它的重量,曹冲想到把它变成称“小石头”的重量,从而知道大象的重量,非常有新意,非常了不起,我想我们同学在今天以及以后的学习中也会像曹冲一样,遇到问题多动脑,多思考,一定能想出解决问题的好办法。下面我们就带着思考来看一组图形。
二、初步感知,体会价值
1.请学生仔细观察,下面两个图形,哪个面积大一些?
(1)
师:哪一个大?为什么?
(2)
2.出示例1。
提问:这两个图形相对复杂一些,你准备怎样比较?先想一想,把你的想法说给同桌听。
学生汇报。
追问:数方格,可以吗?你打算先数什么?再数什么?还有其他方法吗?你这样做的目的是?也就是把不规则的图形转化成规则的图形来比较。
教师:就用你们的方法,可以数一数,也可以把图形变一变,在作业纸上试一试。
学生操作,反馈交流。你是怎样比较的?
预设:数方格,结果是多少?(找3位同学汇报)
变形,你是怎么做的,请上来汇报一下。
为了让所有的同学看清楚,我们用电脑演示一下。
教师电脑演示:[课件演示]把左边这个图形上面的半圆向下平移了8格,变成了长方形;把右边图形的下面两个部分分别向上旋转了180°,变成了长方形。
教师问:转化之后,什么变了?什么没变?
从图上看,这两个图形的面积怎样?你是怎么知道的?(从图上看,这两个图形的面积相等。)
教师:刚才已明确,什么没变?说明原来两个图形的面积相等。
教师提问:刚才在我们解决问题的过程中蕴含了一种重要的数学思想方法(板书:转化),转化是一种很好的解决问题策略,在运用时还需要用到一些具体的方法,刚才在转化的时候我们用了哪些方法?(根据学生的回答板书:平移、旋转)。
教师提问:[课件演示:回到原来的两个图]刚才我们有同学用数方格的方法来比较,结果准确吗?
说明不“转化”,解决这个问题的过程挺复杂的。回顾刚才解决问题的过程,你有什么体会?
预设:(1)为什么刚开始我们看不出这两个图形的面积相等,现在一下子就能看出来呢?(预设:运用“转化”策略,可以让复杂的解决问题过程变得简单。(板书: 复杂 转化 简单 )
(2)观察并回顾刚才的转化过程,什么变了?什么没有变?
三、丰富外延,探寻本质
1.对于转化,其实我们一点都不陌生,在以前的学习过程中,早就运用转化的策略解决了许多问题。比如,我们在不会算平行四边形的面积时,需要推导面积公式时,是怎么做的?(课件演示)现在请你回想一下,我们曾经运用转化的策略还解决过哪些问题?
2.讨论:你们有没有发现,刚才我们举得这些例子,都不约而同地用到了什么策略?都是在什么情况下用了转化的策略?(化未知为已知;化复杂为简单等等)(板书:未知 已知)
3.追问:如果以后你再遇到一个复杂或陌生的问题时,可以怎么想?
下面我们一起去闯关好吗?
四、实践运用,探索方法
1.第一关:小试牛刀(练习十六第1题)
(1)指名读题: 右边图形的周长该怎样计算简便呢?和你的同桌交流一下。
(2)交流反馈:你为什么要转化?怎样转化?课件演示。转化前后什么不能变?(板书 :周长不变)
2.第二关:乘胜追击(练习十六2)
(1)学生独立解答,交流。第一个:你是怎么想的?还可以?这样就更直观的看出涂色部分了。第二个:你是怎么想的?还可以?这两个图形转化前后什么不能变?
(2)重点交流第三个。你是怎么想的?课件辅助为什么十六分之九是错的?让学生上台动手转一转,观察到涂色部分比十六分之九要大些。课件再对比十六分之九与十六分之十。还可以怎样想?课件演示旋转拼摆。还有不同想法吗?思考空白部分。
3.第三关:大显身手(练一练与练习十六3变形拓展)
指名读题。
(1)师:看他们是怎么设计的 这两种设计小路面积相等吗?为什么?那剩下草坪面积也相等。
(2)师:如果长方形长是45米,宽是27米,剩下草坪面积是多少?在练习纸上写一写。集体交流。
(3)如果要想草坪的面积不变,这两条小路还可以怎样设计?为什么?也就是平行于两条长、宽之间的任意一条。小路的设计可以非常的丰富,但无论哪种设计,剩下草坪的面积都是一样的,都可以用这一个算式来表示。
(4)拓展:再增加几条小路,如何求草坪的面积?
五、全课小结
今天这节课我们一起学习了解决问题的策略是转化。你为什么要转化?怎么转化?转化的依据是什么?
