数学高中苏教版必修三第3章《概率》课件
文档属性
| 名称 | 数学高中苏教版必修三第3章《概率》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 164.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-14 18:35:06 | ||
图片预览







文档简介
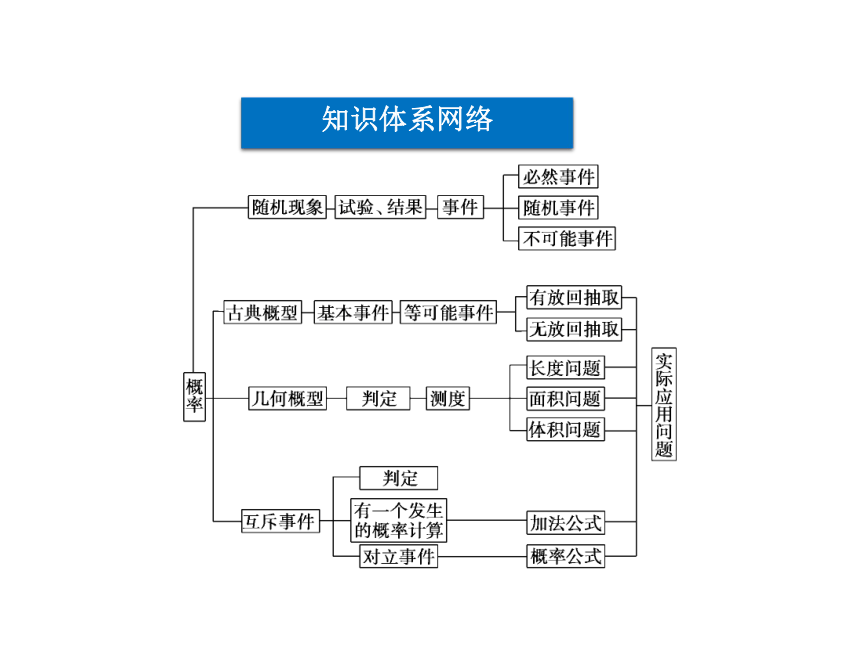
课件22张PPT。本章优化总结 专题探究精讲章末综合检测本章优化总结知识体系网络知识体系网络专题探究精讲随机事件及其概率的概念随机事件在现实世界中是广泛存在的,要注意结合生活实例分析何为必然事件、不可能事件和随机事件,要充分理解概率的意义,并学会解释生活中的一些常见的概率问题,把自己所学的概率知识应用到实际生活中去.在下列六个事件中,随机事件的个数是________.
①如果a,b都是实数,那么a+b=b+a;
②买一张福利彩票,中奖;
③实心铁块丢入水中,铁块浮起;
④掷一枚硬币,正面向上;
⑤在标准大气压下,水的温度达到60 ℃时沸腾;
⑥同性电荷相互排斥.【思路点拨】 紧扣概念.
【解析】 ①⑥为必然事件,②④为随机事件,③⑤为不可能事件,所以答案为2个.
【答案】 2
【题后点评】 本题主要是区分开概念性问题.古典概型同时掷四枚均匀硬币,求:
(1)恰有两枚“正面向上”的概率;
(2)至少有两枚“正面向上”的概率.
【思路点拨】 本题属于等可能事件的概率问题.四枚硬币发生的结果总数我们可以分步确定,恰有两枚正面向上,可以先确定哪两枚正面向上,则另两枚反面向上;至少有两枚正面向上可分类为两枚正面向上、三枚正面向上、全部正面向上.【名师点评】 在运用公式时,关键在于求出m,n,在求n时,应注意所有可能的结果必须是等可能的,这一点比较容易出错.可结合图形采取列举法,列出试验的所有可能结果及事件A包含的所有可能结果.几何概型小明家的晚报在下午5∶30-6∶30之间的任何一个时间随机地被送到,小明一家人在下午6∶00-7∶00之间的任何一个时间随机地开始晚餐.
(1)你认为晚报在晚餐开始之前被送到和在晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少?
【思路点拨】 构造出变量区域,利用几何概型的解法求解.【解】 (1)晚报在5∶30-6∶00之间被送到或晚餐在6∶00-7∶00之间开始,这两种情况都使得晚报在晚餐开始之前被送到.因此晚报在晚餐开始之前被送到的可能性大.
(2)在平面上建立如图所示的坐标系
图中直线x=6,x=7,y=5.5,y=6.5围成一个正方形区域G,设晚餐在x时开始,晚报在y时送达(这里6≤x≤7,5.5≤y≤6.5),这个结果与平面【名师点评】 (1)本题关键是把问题转化为区域图形面积问题;(2)要学会把一些实际问题转化为几何概型.互斥事件与对立事件(1)互斥事件和对立事件是针对两个事件而言的,它们既有区别又有联系.在一次试验中,两个互斥事件有可能都不发生,也可能有一个发生;而两个对立的事件则必有一个发生,但不可能同时发生.(2)当事件A与事件B互斥时,P(A+B)=P(A)+P(B),当事件A与事件B对立时,P(A+B)=P(A)+P(B)=1,即P(A)=1-P(B).
(3)应用互斥事件的概率的加法公式解题时,一定要注意首先确定各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于较复杂事件的概率,可以转化为求对立事件的概率.【思路点拨】 取到红色牌是指取到红心或者取到方片,即C=A+B.又取到红心与取到方片是互斥事件,故可用概率的加法公式求解.取到黑色牌的对立事件是取到红色牌,即C与D是对立事件.【名师点评】 本题考查的是互斥事件与对立事件的概率的求法,其实质是将事件分解成彼此互斥的事件的和,利用互斥事件加法公式求解,或转化为其对立事件的概率求解,体现了化难为易,化繁为简的思想方法.
①如果a,b都是实数,那么a+b=b+a;
②买一张福利彩票,中奖;
③实心铁块丢入水中,铁块浮起;
④掷一枚硬币,正面向上;
⑤在标准大气压下,水的温度达到60 ℃时沸腾;
⑥同性电荷相互排斥.【思路点拨】 紧扣概念.
【解析】 ①⑥为必然事件,②④为随机事件,③⑤为不可能事件,所以答案为2个.
【答案】 2
【题后点评】 本题主要是区分开概念性问题.古典概型同时掷四枚均匀硬币,求:
(1)恰有两枚“正面向上”的概率;
(2)至少有两枚“正面向上”的概率.
【思路点拨】 本题属于等可能事件的概率问题.四枚硬币发生的结果总数我们可以分步确定,恰有两枚正面向上,可以先确定哪两枚正面向上,则另两枚反面向上;至少有两枚正面向上可分类为两枚正面向上、三枚正面向上、全部正面向上.【名师点评】 在运用公式时,关键在于求出m,n,在求n时,应注意所有可能的结果必须是等可能的,这一点比较容易出错.可结合图形采取列举法,列出试验的所有可能结果及事件A包含的所有可能结果.几何概型小明家的晚报在下午5∶30-6∶30之间的任何一个时间随机地被送到,小明一家人在下午6∶00-7∶00之间的任何一个时间随机地开始晚餐.
(1)你认为晚报在晚餐开始之前被送到和在晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少?
【思路点拨】 构造出变量区域,利用几何概型的解法求解.【解】 (1)晚报在5∶30-6∶00之间被送到或晚餐在6∶00-7∶00之间开始,这两种情况都使得晚报在晚餐开始之前被送到.因此晚报在晚餐开始之前被送到的可能性大.
(2)在平面上建立如图所示的坐标系
图中直线x=6,x=7,y=5.5,y=6.5围成一个正方形区域G,设晚餐在x时开始,晚报在y时送达(这里6≤x≤7,5.5≤y≤6.5),这个结果与平面【名师点评】 (1)本题关键是把问题转化为区域图形面积问题;(2)要学会把一些实际问题转化为几何概型.互斥事件与对立事件(1)互斥事件和对立事件是针对两个事件而言的,它们既有区别又有联系.在一次试验中,两个互斥事件有可能都不发生,也可能有一个发生;而两个对立的事件则必有一个发生,但不可能同时发生.(2)当事件A与事件B互斥时,P(A+B)=P(A)+P(B),当事件A与事件B对立时,P(A+B)=P(A)+P(B)=1,即P(A)=1-P(B).
(3)应用互斥事件的概率的加法公式解题时,一定要注意首先确定各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于较复杂事件的概率,可以转化为求对立事件的概率.【思路点拨】 取到红色牌是指取到红心或者取到方片,即C=A+B.又取到红心与取到方片是互斥事件,故可用概率的加法公式求解.取到黑色牌的对立事件是取到红色牌,即C与D是对立事件.【名师点评】 本题考查的是互斥事件与对立事件的概率的求法,其实质是将事件分解成彼此互斥的事件的和,利用互斥事件加法公式求解,或转化为其对立事件的概率求解,体现了化难为易,化繁为简的思想方法.
