4.3原子的核式结构模型(共24张ppt)
文档属性
| 名称 | 4.3原子的核式结构模型(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-28 16:52:00 | ||
图片预览







文档简介
(共24张PPT)
4.3 原子的核式结构模型
问题:科学家在研究稀薄气体放电时发现,当玻璃管内的气体足够稀薄时,阴极就发出一种射线。它能使对着阴极的玻璃管壁发出荧光,这种射线的本质是什么呢?
这种射线称为阴极射线。对这种射线本
质的认识有两种观点:
一种观点认为,它是一种电磁辐射;
另一种观点认为,它是带电微粒。如何用实验判断哪一种观点正确呢?
电子的发现
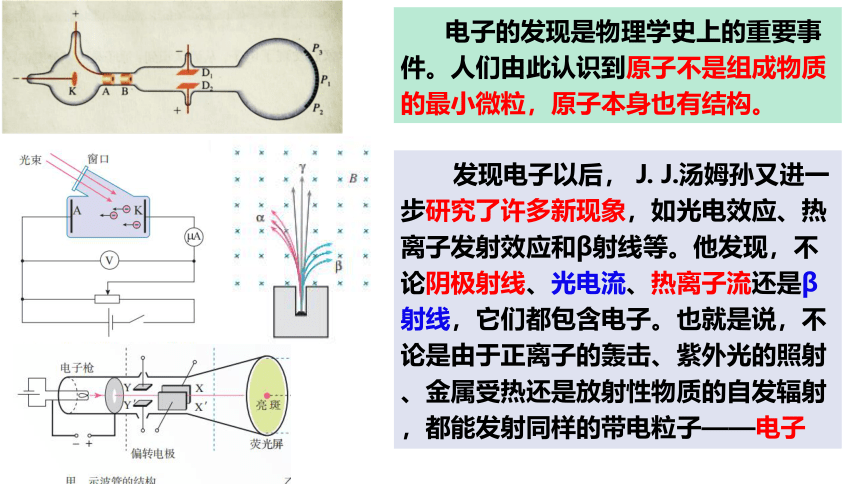
为了证实这一点,从1890年起他和他的助手进行了一系列实验研究。左图是他当时使用的气体放电管的示意图。
当时,两种观点的支持者争执不下,谁也说服不了谁。为了找到有利于自己的证据,双方都做了许多实验。英国物理学家J. J. 汤姆孙认为阴极射线是带电粒子流。
J. J. 汤姆孙气体放电管的示意图。
电子的发现
图中产生阴极射线的机理是:管中残存气体分子中的正负电荷在强电场的作用下被“拉开”(即气体分子被电离),正电荷(即正离子)在电场加速下撞击阴极,于是阴极释放更多粒子流,形成了阴极射线。
由阴极K发出的带电粒子通过缝隙A、B形成一束细细的射线。它穿过两片平行的金属板D1、D2 之间的空间,到达右端带有标尺的荧光屏上。根据射线产生的荧光的位置(如P1,P2,P3,…),可以研究射线的径迹。
J. J. 汤姆孙气体放电管的示意图。
电子的发现
他进一步发现,用不同材料的阴极做实验,所得比荷的数值都是相同的。这说明不同物质都能发射这种带电粒子,它是构成各种物质的共有成分。
1897年,J. J.汤姆孙根据阴极射线在电场和磁场中的偏转情况断定,它的本质是带负电的粒子流,并求出了这
种粒子的比荷。
由实验测得的阴极射线粒子的比荷是氢离子①(也就是质子)比荷的近两千倍。J. J.汤姆孙认为,这可能表示阴极射线粒子电荷量的大小与一个氢离子一样,而质量比氢离子小得多。后来,他直接测到了阴极射线粒子的电荷量,尽管测量不很准确,但足以证明这种粒子电荷量的大小与氢离子大致相同,这就表明他当初的猜测是正确的。后来,组成阴极射线的粒子被称为电子。
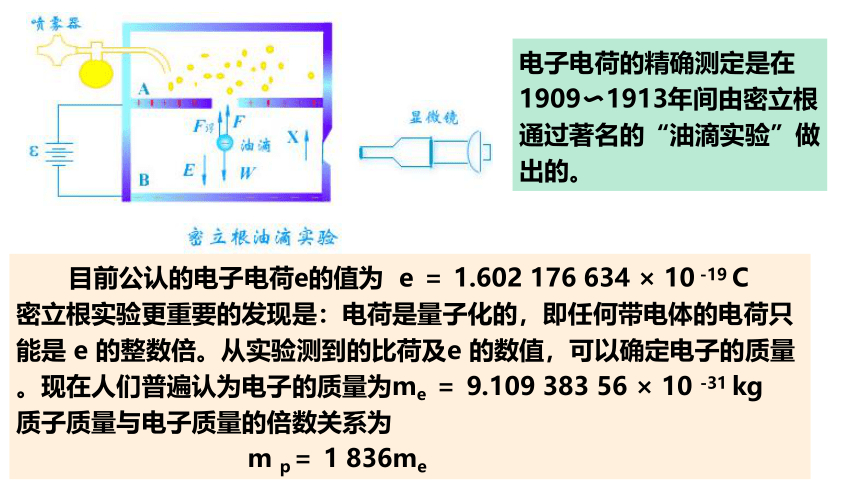
电子电荷的精确测定是在1909 1913年间由密立根通过著名的“油滴实验”做出的。
目前公认的电子电荷e的值为 e = 1.602 176 634 × 10 -19 C
密立根实验更重要的发现是:电荷是量子化的,即任何带电体的电荷只能是 e 的整数倍。从实验测到的比荷及e 的数值,可以确定电子的质量。现在人们普遍认为电子的质量为me = 9.109 383 56 × 10 -31 kg
质子质量与电子质量的倍数关系为
m p= 1 836me
发现电子以后, J. J.汤姆孙又进一步研究了许多新现象,如光电效应、热离子发射效应和β射线等。他发现,不
论阴极射线、光电流、热离子流还是β射线,它们都包含电子。也就是说,不论是由于正离子的轰击、紫外光的照射、金属受热还是放射性物质的自发辐射,都能发射同样的带电粒子——电子
电子的发现是物理学史上的重要事件。人们由此认识到原子不是组成物质
的最小微粒,原子本身也有结构。
电子的发现
J. J.汤姆孙对证实电子的存在有很大贡献,因此公认他是电子的发现者。他因气体导电的研究获得1906年的诺贝尔物理学奖。
原子中带正电的部分以及带负电的电子可能是如何分布的呢?
思考与讨论:通常情况下,物质是不带电的,因此,原子应该是电中性的。既然电子是带负电的,质量又很小,那么,原子中一定还有带正电的部分,而且它应该具有大部分的原子质量。
英国物理学家
汤姆孙
汤姆孙原子模型(枣糕模型)
汤姆孙的原子模型
在J. J. 汤姆孙发现电子之后,对于原子中正负电荷如何分布的问题,科学家们提出了许多模型。J. J. 汤姆孙本人于 1898 年提出了一种模型。
他认为,原子是一个球体,正电荷弥漫性地均匀分布在整个球体内,电子镶嵌其中(图4.3-2)。有人形象地把他的这个模型称为“西瓜模型”或“枣糕模型”
英国物理学家
汤姆孙
汤姆孙原子模型(枣糕模型)
汤姆孙的原子模型“枣糕模型”
这个模型能够解释一些实验现象。但德国物理学家勒纳德 1903 年做了一个实验,使电子束射到金属膜上,发现较高速度的电子很容易穿透原子。
这说明原子不是一个实心球体,这个“枣糕模型”可能不正确。之后不久,α 粒子散射实验则完全否定了这个模型
原子的核式结构模型
粒子散射实验 α 粒子是从放射性物质(如铀和镭)中发射出来的快速运动的粒子,质量为氢原子质量的 4 倍、电子质量的 7 300 倍。
1909 年,英国物理学家卢瑟福指导他的助手盖革和马斯顿进行 α 粒子散射实验的研究时,所用仪器的示意图如图所示。
粒子散射实验 α 粒子源 R 是被铅块包围的,它发射的 α 粒子经过一条细通道,形成一束射线,打在金箔 F 上。显微镜 M 带有荧光屏 S ,可以在水平面内转到不同的方向对散射的 α 粒子进行观察。
被散射的 α 粒子打在荧光屏上会有微弱的闪光产生。通过显微镜观察闪光就可以记录在某一时间内向某一方向散射的 α 粒子数。
粒子散射实验 从 α 粒子放射源到荧光屏这段路程处于真空中。
当 α 粒子打到金箔时,由于金原子中的带电粒子对α 粒子有库仑力的作用,一些 α 粒子的运动方向改变,也就是发生了 α 粒子的散射。
统计散射到各个方向的 α 粒子
所占的比例,可以推知原子中电荷的分布情况。除了金箔,当时的实验还用了其他重金属箔,例如铂箔
思考与讨论: 1. α粒子射入金箔时难免与电子碰撞。试估计这种碰撞对α粒子速度影响的大小。2. 按照J. J.汤姆孙的原子模型,正电荷均匀分布在整个原子球体内。请分析:α粒子穿过金箔,受到电荷的作用力后,沿哪些方向前进的可能性较大,最不可能沿哪些方向前进
按照J. J. 汤姆孙的模型α 粒子穿过原子时受到的各方向正电荷的斥力基本上会相互平衡,因此对 α 粒子运动的影响不会很大。α粒子穿过金箔后,沿原来的方向前进的可能性较大
实验发现,绝大多数α粒子穿过金箔后,基本上仍沿原来的方向前进,但有少数α粒子(约占 1/8 000 )发生了大角度偏转,极少数偏转的角度甚至大于90°,也就是说,它们几乎被“撞了回来”
对 α 粒子散射实验的解释 这样的事实令人惊奇。大角度的偏转不可能是电子造成的,因为它的质量只有 α 粒子的 1/7 300 ,它对 α 粒子速度的大小和方向的影响就像灰尘对枪弹的影响,完全可以忽略。
因此,α 粒子偏转主要是具有原子的大部分质量的带正电部分造成的。所以,J. J. 汤姆孙的模型无法解释大角度散射的实验结果。
对 α 粒子散射实验的解释 卢瑟福分析了实验数据后认为,事实应该是:占原子质量绝大部分的带正电的物质集中在很小的空间范围。这样才会使α粒子在经过时受到很强的斥力,使其发生大角度的偏转。
1911 年,卢瑟福提出了自己的原子结构模型。他设想:原子中带正电部分的体积很小,但几乎占有全部质量,电子在正电体的外面运动。这样,当α粒子接近原子时,电子对它的影响仍如前述可以忽略,但是,正电体对它的作用就不同了。因为正电体很小,当α粒子进入原子区域后,大部分离正电体很远,受到的库仑斥力很小,运动方向几乎不改变。只有极少数α粒子在穿过时距离正电体很近,因此受到很强的库仑斥力,发生大角度散射。这个情况如图4.3-4所示。
按照卢瑟福的理论,正电体的尺度是很小的,称为原子核。卢瑟福的原子模型因而称为原子的核式结构模型。卢瑟福以这个模型为依据,利用经典力学计算了向各个方向散射的α粒子的比例,结果与实验数据符合得很好。
原子核的电荷与尺度
由不同元素对α粒子散射的实验数据可以确定不同元素原子核的电荷量Q又由于原子是电中性的,可以推算出原子内含有的电子数。
科学家们注意到,各种元素的原子核的电荷数,即原子内的电子数,非常接近它们的原子
序数,这说明元素周期表中的各种元素是按原子中的电子数来排列的
原子核的电荷与尺度
现在,我们知道,原子确实是由带电荷+Ze 的核与核外Z 个电子组成的。原子序数Z 等于核电荷与电子电荷大小的比值。它表示原子核的电荷是一个电子电荷量的多少倍。后来又发现原子核是由质子和中子组成的,原子核的电荷数就是核中的质子数。
Ze 是原子核的电荷,单位是库仑;Z 是原子序数,也叫核电荷数,它表示原子核的电荷是一个电子电荷(绝对值)的多少倍。Z是没有单位的,或者说 Z 的单位是 1。
原子核的电荷与尺度
通常用核半径描述核的大小。原子核的半径是很难测量的,一般通过其他粒子与核的相互作用来确定。α粒子散射可以用来估算核半径。对于一般的原子核,实验确定的核半径的数量级为10-15 m,而整个原子半径的数量级是10-10m,两者相差十万倍之多。可见原子内部是十分“空旷”的
4.3 原子的核式结构模型
问题:科学家在研究稀薄气体放电时发现,当玻璃管内的气体足够稀薄时,阴极就发出一种射线。它能使对着阴极的玻璃管壁发出荧光,这种射线的本质是什么呢?
这种射线称为阴极射线。对这种射线本
质的认识有两种观点:
一种观点认为,它是一种电磁辐射;
另一种观点认为,它是带电微粒。如何用实验判断哪一种观点正确呢?
电子的发现
为了证实这一点,从1890年起他和他的助手进行了一系列实验研究。左图是他当时使用的气体放电管的示意图。
当时,两种观点的支持者争执不下,谁也说服不了谁。为了找到有利于自己的证据,双方都做了许多实验。英国物理学家J. J. 汤姆孙认为阴极射线是带电粒子流。
J. J. 汤姆孙气体放电管的示意图。
电子的发现
图中产生阴极射线的机理是:管中残存气体分子中的正负电荷在强电场的作用下被“拉开”(即气体分子被电离),正电荷(即正离子)在电场加速下撞击阴极,于是阴极释放更多粒子流,形成了阴极射线。
由阴极K发出的带电粒子通过缝隙A、B形成一束细细的射线。它穿过两片平行的金属板D1、D2 之间的空间,到达右端带有标尺的荧光屏上。根据射线产生的荧光的位置(如P1,P2,P3,…),可以研究射线的径迹。
J. J. 汤姆孙气体放电管的示意图。
电子的发现
他进一步发现,用不同材料的阴极做实验,所得比荷的数值都是相同的。这说明不同物质都能发射这种带电粒子,它是构成各种物质的共有成分。
1897年,J. J.汤姆孙根据阴极射线在电场和磁场中的偏转情况断定,它的本质是带负电的粒子流,并求出了这
种粒子的比荷。
由实验测得的阴极射线粒子的比荷是氢离子①(也就是质子)比荷的近两千倍。J. J.汤姆孙认为,这可能表示阴极射线粒子电荷量的大小与一个氢离子一样,而质量比氢离子小得多。后来,他直接测到了阴极射线粒子的电荷量,尽管测量不很准确,但足以证明这种粒子电荷量的大小与氢离子大致相同,这就表明他当初的猜测是正确的。后来,组成阴极射线的粒子被称为电子。
电子电荷的精确测定是在1909 1913年间由密立根通过著名的“油滴实验”做出的。
目前公认的电子电荷e的值为 e = 1.602 176 634 × 10 -19 C
密立根实验更重要的发现是:电荷是量子化的,即任何带电体的电荷只能是 e 的整数倍。从实验测到的比荷及e 的数值,可以确定电子的质量。现在人们普遍认为电子的质量为me = 9.109 383 56 × 10 -31 kg
质子质量与电子质量的倍数关系为
m p= 1 836me
发现电子以后, J. J.汤姆孙又进一步研究了许多新现象,如光电效应、热离子发射效应和β射线等。他发现,不
论阴极射线、光电流、热离子流还是β射线,它们都包含电子。也就是说,不论是由于正离子的轰击、紫外光的照射、金属受热还是放射性物质的自发辐射,都能发射同样的带电粒子——电子
电子的发现是物理学史上的重要事件。人们由此认识到原子不是组成物质
的最小微粒,原子本身也有结构。
电子的发现
J. J.汤姆孙对证实电子的存在有很大贡献,因此公认他是电子的发现者。他因气体导电的研究获得1906年的诺贝尔物理学奖。
原子中带正电的部分以及带负电的电子可能是如何分布的呢?
思考与讨论:通常情况下,物质是不带电的,因此,原子应该是电中性的。既然电子是带负电的,质量又很小,那么,原子中一定还有带正电的部分,而且它应该具有大部分的原子质量。
英国物理学家
汤姆孙
汤姆孙原子模型(枣糕模型)
汤姆孙的原子模型
在J. J. 汤姆孙发现电子之后,对于原子中正负电荷如何分布的问题,科学家们提出了许多模型。J. J. 汤姆孙本人于 1898 年提出了一种模型。
他认为,原子是一个球体,正电荷弥漫性地均匀分布在整个球体内,电子镶嵌其中(图4.3-2)。有人形象地把他的这个模型称为“西瓜模型”或“枣糕模型”
英国物理学家
汤姆孙
汤姆孙原子模型(枣糕模型)
汤姆孙的原子模型“枣糕模型”
这个模型能够解释一些实验现象。但德国物理学家勒纳德 1903 年做了一个实验,使电子束射到金属膜上,发现较高速度的电子很容易穿透原子。
这说明原子不是一个实心球体,这个“枣糕模型”可能不正确。之后不久,α 粒子散射实验则完全否定了这个模型
原子的核式结构模型
粒子散射实验 α 粒子是从放射性物质(如铀和镭)中发射出来的快速运动的粒子,质量为氢原子质量的 4 倍、电子质量的 7 300 倍。
1909 年,英国物理学家卢瑟福指导他的助手盖革和马斯顿进行 α 粒子散射实验的研究时,所用仪器的示意图如图所示。
粒子散射实验 α 粒子源 R 是被铅块包围的,它发射的 α 粒子经过一条细通道,形成一束射线,打在金箔 F 上。显微镜 M 带有荧光屏 S ,可以在水平面内转到不同的方向对散射的 α 粒子进行观察。
被散射的 α 粒子打在荧光屏上会有微弱的闪光产生。通过显微镜观察闪光就可以记录在某一时间内向某一方向散射的 α 粒子数。
粒子散射实验 从 α 粒子放射源到荧光屏这段路程处于真空中。
当 α 粒子打到金箔时,由于金原子中的带电粒子对α 粒子有库仑力的作用,一些 α 粒子的运动方向改变,也就是发生了 α 粒子的散射。
统计散射到各个方向的 α 粒子
所占的比例,可以推知原子中电荷的分布情况。除了金箔,当时的实验还用了其他重金属箔,例如铂箔
思考与讨论: 1. α粒子射入金箔时难免与电子碰撞。试估计这种碰撞对α粒子速度影响的大小。2. 按照J. J.汤姆孙的原子模型,正电荷均匀分布在整个原子球体内。请分析:α粒子穿过金箔,受到电荷的作用力后,沿哪些方向前进的可能性较大,最不可能沿哪些方向前进
按照J. J. 汤姆孙的模型α 粒子穿过原子时受到的各方向正电荷的斥力基本上会相互平衡,因此对 α 粒子运动的影响不会很大。α粒子穿过金箔后,沿原来的方向前进的可能性较大
实验发现,绝大多数α粒子穿过金箔后,基本上仍沿原来的方向前进,但有少数α粒子(约占 1/8 000 )发生了大角度偏转,极少数偏转的角度甚至大于90°,也就是说,它们几乎被“撞了回来”
对 α 粒子散射实验的解释 这样的事实令人惊奇。大角度的偏转不可能是电子造成的,因为它的质量只有 α 粒子的 1/7 300 ,它对 α 粒子速度的大小和方向的影响就像灰尘对枪弹的影响,完全可以忽略。
因此,α 粒子偏转主要是具有原子的大部分质量的带正电部分造成的。所以,J. J. 汤姆孙的模型无法解释大角度散射的实验结果。
对 α 粒子散射实验的解释 卢瑟福分析了实验数据后认为,事实应该是:占原子质量绝大部分的带正电的物质集中在很小的空间范围。这样才会使α粒子在经过时受到很强的斥力,使其发生大角度的偏转。
1911 年,卢瑟福提出了自己的原子结构模型。他设想:原子中带正电部分的体积很小,但几乎占有全部质量,电子在正电体的外面运动。这样,当α粒子接近原子时,电子对它的影响仍如前述可以忽略,但是,正电体对它的作用就不同了。因为正电体很小,当α粒子进入原子区域后,大部分离正电体很远,受到的库仑斥力很小,运动方向几乎不改变。只有极少数α粒子在穿过时距离正电体很近,因此受到很强的库仑斥力,发生大角度散射。这个情况如图4.3-4所示。
按照卢瑟福的理论,正电体的尺度是很小的,称为原子核。卢瑟福的原子模型因而称为原子的核式结构模型。卢瑟福以这个模型为依据,利用经典力学计算了向各个方向散射的α粒子的比例,结果与实验数据符合得很好。
原子核的电荷与尺度
由不同元素对α粒子散射的实验数据可以确定不同元素原子核的电荷量Q又由于原子是电中性的,可以推算出原子内含有的电子数。
科学家们注意到,各种元素的原子核的电荷数,即原子内的电子数,非常接近它们的原子
序数,这说明元素周期表中的各种元素是按原子中的电子数来排列的
原子核的电荷与尺度
现在,我们知道,原子确实是由带电荷+Ze 的核与核外Z 个电子组成的。原子序数Z 等于核电荷与电子电荷大小的比值。它表示原子核的电荷是一个电子电荷量的多少倍。后来又发现原子核是由质子和中子组成的,原子核的电荷数就是核中的质子数。
Ze 是原子核的电荷,单位是库仑;Z 是原子序数,也叫核电荷数,它表示原子核的电荷是一个电子电荷(绝对值)的多少倍。Z是没有单位的,或者说 Z 的单位是 1。
原子核的电荷与尺度
通常用核半径描述核的大小。原子核的半径是很难测量的,一般通过其他粒子与核的相互作用来确定。α粒子散射可以用来估算核半径。对于一般的原子核,实验确定的核半径的数量级为10-15 m,而整个原子半径的数量级是10-10m,两者相差十万倍之多。可见原子内部是十分“空旷”的
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
