数学高中苏教版必修三2.3.2《方差与标准差》课件
文档属性
| 名称 | 数学高中苏教版必修三2.3.2《方差与标准差》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-14 18:50:23 | ||
图片预览







文档简介
课件29张PPT。2.3.2 方差与标准差学习目标
1.会求样本标准差、方差;
2.理解用样本的数字特征来估计总体数字特征的方法;
3.会应用相关知识解决简单的统计实际问题. 课堂互动讲练知能优化训练2.3.2 方差与标准差课前自主学案课前自主学案通过上节知识的学习,你能体会出众数、中位数、平均数这三种数字特征的优缺点吗?
1.众数体现了样本数据的最大集中点,但它对其他数据信息的忽视使得无法客观地反映总体特征.
2.中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点.3.由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具备的性质.也正因为这个原因,与众数、中位数比较起来,平均数可以反映出更多的关于全体样本数据的信息.但平均数受数据中的极端值的影响较大,使平均数在估计总体时可靠性降低.1.极差
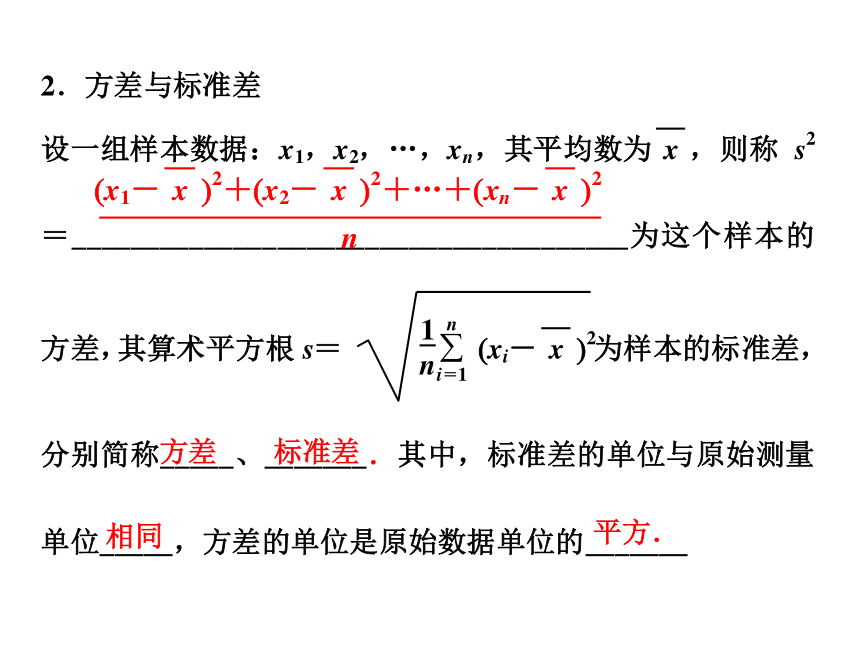
一组数据的_______与________的_____最大值最小值差.方差标准差相同平方.3.方差和标准差的意义
方差和标准差都是用来描述_________________
__________,常用来比较两组数据的波动大小,我们所研究的仅是这两组数据的个数相等,平均数相等或比较接近时的情况.
方差较大的波动较大,方差较小的波动较小.样本平均数和方差、标准差描述了样本数据的什么特征?
提示:样本平均数是刻画一组数据集中趋势最常用的统计量,描述了样本数据的平均水平.样本方差和标准差是刻画数据的离散程度的量,方差越大,离散程度越大.课堂互动讲练极差、平均数、方差与标准差的概念对概念的理解应注意以下两点:
(1)方差、标准差描述了一组数据围绕平均数波动的大小.方差、标准差越大,数据越分散;方差、标准差越小,数据越集中(若s=0,则表明数据没有波动,样本数据全相等).
(2)样本的平均数和方差是两个重要的数字特征.在应用平均数和方差解决实际问题时,若平均数不同,则直接应用平均数比较;若平均数相同,则要由方差、标准差研究其与平均数的偏离程度. 下列叙述不正确的是______.
①样本的平均数可以近似地描述总体的平均水平
②极差描述了一组数据变化的幅度
③样本的方差描述了一组数据围绕平均数波动的大小
④一个班级的数学成绩的方差越大说明成绩越稳定【思路点拨】 本题主要考察对样本的平均数,极差,方差的理解,可用定义判断正误.
【解析】 选项①、②、③都是对三个基本概念的正确描述,方差越大说明一组数据围绕平均数的波动越大,所以,一个班级的数学成绩的方差越大说明成绩越不稳定,因此选项④是不正确的.故选④.
【答案】 ④
【名师点评】 通过本题可以加深对概念性问题的理解.自我挑战1 下列说法正确的是______.
①甲、乙两个班期末考试数学平均成绩相同,这表明这两个班数学学习情况一样;
②期末考试数学成绩的方差甲班比乙班的小,这表明甲班的数学学习情况比乙班好;
③期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班大,则数学学习情况甲班比乙班好;
④期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班小,则数学学习情况甲班比乙班好.
答案:④ 已知一个样本为1,3,2,5,x,它的平均数是3,则这个样本的标准差是多少?【名师点评】 (1)标准差公式及变形要记忆牢固,运用熟练.
(2)方差、标准差单位不一致,要注意区别.答案:4 3(1)在计算平均数和标准差时,如果数据较大,可以注意方法的选择,将各个数据都减去同一个数后,平均数也相应减小了,而这组数据的标准差不会发生变化.
(2)平均数与标准差都是重要的数字特征数,是对总体的一种简明的描述.它们所反映的情况有着重要的实际意义,所以,不仅需要掌握其计算公式和方法,还要学会通过这些数据分析其含义,从而为正确决策提供依据. (本题满分14分)甲、乙两名战士在相同条件下各射靶10次,每次命中的环数分别是(单位:环):
甲:8,6,7,8,6,5,9,10,4,7;
乙:6,7,7,8,6,7,8,7,9,5.
(1)分别计算以上两组数据的平均数;
(2)分别求出两组数据的标准差;
(3)根据计算结果,估计一下两名战士的射击情况.
【思路点拨】 把数据直接代入公式求解,进而根据代表的含义估计两名战士的射击情况.【名师点评】 (1)在解答本题(3)时,易出现对甲、乙射击情况判断的错误,要正确理解方差的概念.
(2)解决此类题目,需要有把握数据的能力,通过观察、分析、计算,进而比较平均数和方差的大小,从数学理论角度出发,用数据说话,问题不难得到解决.自我挑战3 两台机床同时生产直径为10的零件,为了检验产品的质量,质量检验员从两台机床的产品中各抽出4件进行测量,结果如下:
机床甲:10 9.8 10 10.2
机床乙:10.1 10 9.9 10
如果你是质量检验员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求?1.数据的离散程度可以通过极差、方差或标准差来描述.极差反映了一组数据的变化的最大幅度,它对一组数据中的极端值非常敏感.方差则反映了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度,通常用标准差——样本方差的算术平方根来描述.
2.标准差的大小不会越过极差.3.标准差、极差的取值范围:[0,+∞).当标准差、方差为0时,样本各数据全相等,表明数据没有波动幅度,数据没有离散性.
4.因为方差与原始数据的单位不同,且平方后可能夸大了偏差的程度,所以虽然方差和标准差在刻画样本数据的分散程度上是一样的,但在解决实际问题时,一般采用标准差.
1.会求样本标准差、方差;
2.理解用样本的数字特征来估计总体数字特征的方法;
3.会应用相关知识解决简单的统计实际问题. 课堂互动讲练知能优化训练2.3.2 方差与标准差课前自主学案课前自主学案通过上节知识的学习,你能体会出众数、中位数、平均数这三种数字特征的优缺点吗?
1.众数体现了样本数据的最大集中点,但它对其他数据信息的忽视使得无法客观地反映总体特征.
2.中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也会成为缺点.3.由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具备的性质.也正因为这个原因,与众数、中位数比较起来,平均数可以反映出更多的关于全体样本数据的信息.但平均数受数据中的极端值的影响较大,使平均数在估计总体时可靠性降低.1.极差
一组数据的_______与________的_____最大值最小值差.方差标准差相同平方.3.方差和标准差的意义
方差和标准差都是用来描述_________________
__________,常用来比较两组数据的波动大小,我们所研究的仅是这两组数据的个数相等,平均数相等或比较接近时的情况.
方差较大的波动较大,方差较小的波动较小.样本平均数和方差、标准差描述了样本数据的什么特征?
提示:样本平均数是刻画一组数据集中趋势最常用的统计量,描述了样本数据的平均水平.样本方差和标准差是刻画数据的离散程度的量,方差越大,离散程度越大.课堂互动讲练极差、平均数、方差与标准差的概念对概念的理解应注意以下两点:
(1)方差、标准差描述了一组数据围绕平均数波动的大小.方差、标准差越大,数据越分散;方差、标准差越小,数据越集中(若s=0,则表明数据没有波动,样本数据全相等).
(2)样本的平均数和方差是两个重要的数字特征.在应用平均数和方差解决实际问题时,若平均数不同,则直接应用平均数比较;若平均数相同,则要由方差、标准差研究其与平均数的偏离程度. 下列叙述不正确的是______.
①样本的平均数可以近似地描述总体的平均水平
②极差描述了一组数据变化的幅度
③样本的方差描述了一组数据围绕平均数波动的大小
④一个班级的数学成绩的方差越大说明成绩越稳定【思路点拨】 本题主要考察对样本的平均数,极差,方差的理解,可用定义判断正误.
【解析】 选项①、②、③都是对三个基本概念的正确描述,方差越大说明一组数据围绕平均数的波动越大,所以,一个班级的数学成绩的方差越大说明成绩越不稳定,因此选项④是不正确的.故选④.
【答案】 ④
【名师点评】 通过本题可以加深对概念性问题的理解.自我挑战1 下列说法正确的是______.
①甲、乙两个班期末考试数学平均成绩相同,这表明这两个班数学学习情况一样;
②期末考试数学成绩的方差甲班比乙班的小,这表明甲班的数学学习情况比乙班好;
③期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班大,则数学学习情况甲班比乙班好;
④期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班小,则数学学习情况甲班比乙班好.
答案:④ 已知一个样本为1,3,2,5,x,它的平均数是3,则这个样本的标准差是多少?【名师点评】 (1)标准差公式及变形要记忆牢固,运用熟练.
(2)方差、标准差单位不一致,要注意区别.答案:4 3(1)在计算平均数和标准差时,如果数据较大,可以注意方法的选择,将各个数据都减去同一个数后,平均数也相应减小了,而这组数据的标准差不会发生变化.
(2)平均数与标准差都是重要的数字特征数,是对总体的一种简明的描述.它们所反映的情况有着重要的实际意义,所以,不仅需要掌握其计算公式和方法,还要学会通过这些数据分析其含义,从而为正确决策提供依据. (本题满分14分)甲、乙两名战士在相同条件下各射靶10次,每次命中的环数分别是(单位:环):
甲:8,6,7,8,6,5,9,10,4,7;
乙:6,7,7,8,6,7,8,7,9,5.
(1)分别计算以上两组数据的平均数;
(2)分别求出两组数据的标准差;
(3)根据计算结果,估计一下两名战士的射击情况.
【思路点拨】 把数据直接代入公式求解,进而根据代表的含义估计两名战士的射击情况.【名师点评】 (1)在解答本题(3)时,易出现对甲、乙射击情况判断的错误,要正确理解方差的概念.
(2)解决此类题目,需要有把握数据的能力,通过观察、分析、计算,进而比较平均数和方差的大小,从数学理论角度出发,用数据说话,问题不难得到解决.自我挑战3 两台机床同时生产直径为10的零件,为了检验产品的质量,质量检验员从两台机床的产品中各抽出4件进行测量,结果如下:
机床甲:10 9.8 10 10.2
机床乙:10.1 10 9.9 10
如果你是质量检验员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求?1.数据的离散程度可以通过极差、方差或标准差来描述.极差反映了一组数据的变化的最大幅度,它对一组数据中的极端值非常敏感.方差则反映了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度,通常用标准差——样本方差的算术平方根来描述.
2.标准差的大小不会越过极差.3.标准差、极差的取值范围:[0,+∞).当标准差、方差为0时,样本各数据全相等,表明数据没有波动幅度,数据没有离散性.
4.因为方差与原始数据的单位不同,且平方后可能夸大了偏差的程度,所以虽然方差和标准差在刻画样本数据的分散程度上是一样的,但在解决实际问题时,一般采用标准差.
