数学高中苏教版必修三1.2.1《顺序结构》课件
文档属性
| 名称 | 数学高中苏教版必修三1.2.1《顺序结构》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 154.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-14 00:00:00 | ||
图片预览







文档简介
课件25张PPT。1.2 流程图
?1.2.1 顺序结构学习目标1.了解流程图的含义及其构成;
2.能用流程图表示顺序结构. 课堂互动讲练知能优化训练1.2.1 顺序结构课前自主学案课前自主学案1.你还记得算法的特征吗?有限性、确定性、可行性.
2.你明白数学中的算法和生活中的算法的区别了吗?
数学中的算法与生活中的算法的根本区别是数学中的算法是计算机可以执行的.1.流程图
(1)流程图的概念
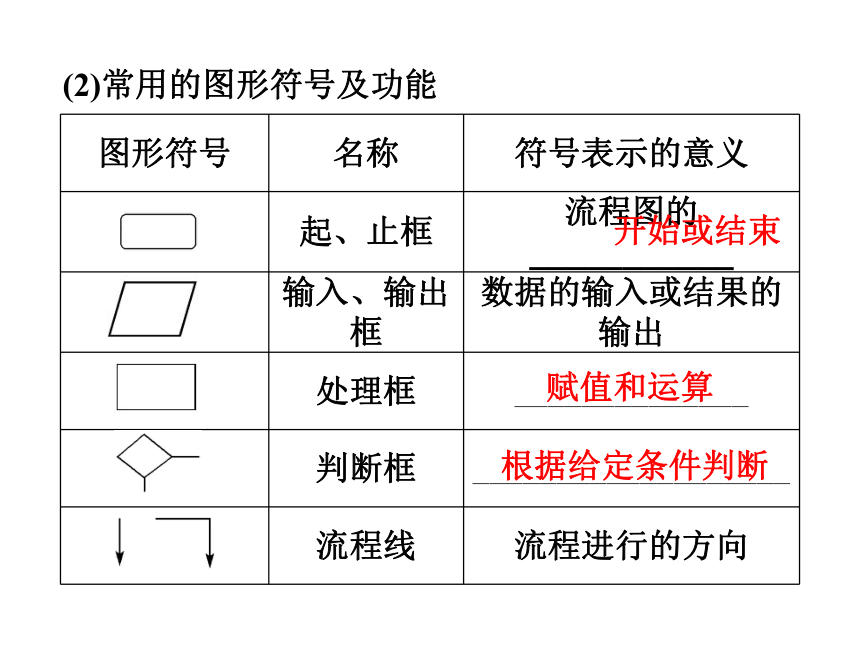
流程图是由一些_____和________________组成的,其中图框表示各种操作的_____,图框中的文字和符号表示______________,带箭头的流程线表示__________________图框带箭头的流程线类型操作的内容操作的先后次序.(2)常用的图形符号及功能 开始或结束赋值和运算根据给定条件判断2.顺序结构
(1)顺序结构的定义依次进行_________的结构称为顺序结构.
(2)结构形式多个处理用流程图表示算法,相对于自然语言描述的算法有什么优点?
提示:流程图相对于自然语言表述算法,看起来更清晰,更明确,也更接近于计算机的程序设计.课堂互动讲练流程图的概念(1)流程图(又称程序框图),是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.
(2)画流程图时要严格遵循画法规则,符号规范,每一个符号的作用明确,让别人一看就懂. 下列关于流程图的图形符号的理解,正确的有________.
①任何一个流程图都必须有起、止框;
②输入框只能放在开始框后,输出框只能放在结束框前;
③判断框是惟一具有超过一个退出点的图形符号;
④对于一个程序来说,判断框内的条件是惟一的.
【思路点拨】 对叙述逐一分析→判断正误→给出结论.【解析】 根据流程图的概念及图形符号的功能进行判断.任何一个程序都必须有开始和结束,从而必须有起、止框;输入和输出框可以用在算法中任何需要输入、输出的位置;判断框内的条件不是惟一的,如“a>b”也可写成“a≤b”此时其它部分需作相应调整,故正确答案为①③.
【答案】 ①③【名师点评】 深刻理解图形符号的含义及其功能是解决这类问题的关键.自我挑战1 下列有关流程图的叙述中,正确的是________.
?卓越品质源于永不满足—————————————————————————优化方案·成功相伴?①流程图中的图形符号可以由个人来确定;
②输入框可以在起始框后,也可以在判断框后;
③◇可以用来执行计算语句;
④用流程图表达算法的优点是算法的基本逻辑结构展现得非常直接.
解析:流程图中的图形符号是统一规定的;◇用来表示判断框.
答案:②④用顺序结构表示算法(1)顺序结构是由若干个依次执行的步骤组成的,它是任何一个算法都离不开的最简单、最基本的结构.
(2)顺序结构只能解决简单问题,它按从上到下的顺序执行,不含程序步骤的跳转. (本题满分14分)计算下列梯形的面积:上底为3,下底为7,高为6.试设计该问题的算法并画出流程图.
【思路点拨】 利用梯形面积公式直接代入计算即可.【名师点评】 (1)要注意各种图形符号的正确使用.(2)本例的算法及流程图具有代表性,能运用于其他很多套用公式的题目,其步骤是先赋值,再运算,最后输出结果.顺序结构的特征及应用(1)用自然语言表述算法步骤;
(2)确定每一个算法步骤所包含的逻辑结构,并用相应的流程图表示,得到该步骤的流程图;
(3)将所有步骤的流程图用流程线连接起来,并加上起止框,得到表示整个算法的流程图. 如图所示是为解决某个问题而绘制的流程图,仔细分析各图框内的内容及图框之间的关系,回答下面的问题:(1)该流程图解决的是怎样的一个问题?
(2)若最终输出的结果y1=3,y2=-2,当x取5时输出的结果5a+b的值应该是多大?
(3)在(2)的前提下,输入的x值越大,输出的ax+b是不是越大?为什么?
(4)在(2)的前提下,当输入的x值为多大时,输出结果ax+b等于0?
【思路点拨】 仔细阅读每个图框中的信息,并结合对每种图框的功能及意义的理解,从而分析总结出该图框所要解决的问题.【解】 (1)该流程图解决的是求函数f(x)=ax+b的函数值的问题.
(2)y1=3,即2a+b=3,①
y2=-2,即-3a+b=-2,②
由①②得a=1,b=1.∴f(x)=x+1.
∴当x取5时,5a+b=f(5)=5+1=6.
(3)输入的x值越大,输出的函数值ax+b越大,
因为f(x)=x+1是R上的增函数.
(4)令f(x)=x+1=0,得x=-1,
因此当输入的x值为-1时,输出的函数值为0.【名师点评】 本题通过探究流程图中每个图框的意义,使学生加深对流程框图的概念及意义的理解,本题中流程框图是采用的顺序结构,因此,我们可以根据流程线的顺序对图框进行逐个分析.自我挑战2 如图所示的流程图,根据该图和下列各小题的条件回答问题.(1)该流程图解决的是一个什么问题?
(2)当输入的x值为0和4时,输出的值相等,问当输入的x的值为3时,输出的值为多大?
(3)在(2)的前提下,要想使输出的值最大,输入的x的值应为多大?
(4)在(2)的前提下,按照这个流程图,当x值都大于2时,x值大的输出的y值反而小,为什么?
(5)在(2)的前提下,要想使输出的值等于3,输入的x应是多少?
(6)在(2)的前提下,要想使输入的值与输出的值相等,输入的值应是多大?解:(1)流程图解决的是求函数f(x)=-x2+mx的函数值的问题,其中输入的是自变量x的值,输出的是x对应的函数值.
(2)因为x=0或x=4时,y值相等,所以m=4,
所以x=3时,y=-32+4×3=-9+12=3.
(3)y=-x2+4x=-(x-2)2+4,
∴当输入的x值为2时,输出的值最大.
(4)当x>2时,y=-(x-2)2+4为减函数,
所以x增大时,输出的y值反而小.
(5)∵y=-x2+4x=3,∴x=1或3.
(6)∵-x2+4x=x,∴x2-3x=0,∴x=0或x=3.1.(1)流程图的每一种图形符号都有特定的含义,在画流程图时不能混用;
(2)在画流程图前,一般先用自然语言编写算法.
2.顺序结构中强调“依次处理”,“从上到下”依次进行每一步,不能“回头”.
?1.2.1 顺序结构学习目标1.了解流程图的含义及其构成;
2.能用流程图表示顺序结构. 课堂互动讲练知能优化训练1.2.1 顺序结构课前自主学案课前自主学案1.你还记得算法的特征吗?有限性、确定性、可行性.
2.你明白数学中的算法和生活中的算法的区别了吗?
数学中的算法与生活中的算法的根本区别是数学中的算法是计算机可以执行的.1.流程图
(1)流程图的概念
流程图是由一些_____和________________组成的,其中图框表示各种操作的_____,图框中的文字和符号表示______________,带箭头的流程线表示__________________图框带箭头的流程线类型操作的内容操作的先后次序.(2)常用的图形符号及功能 开始或结束赋值和运算根据给定条件判断2.顺序结构
(1)顺序结构的定义依次进行_________的结构称为顺序结构.
(2)结构形式多个处理用流程图表示算法,相对于自然语言描述的算法有什么优点?
提示:流程图相对于自然语言表述算法,看起来更清晰,更明确,也更接近于计算机的程序设计.课堂互动讲练流程图的概念(1)流程图(又称程序框图),是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.
(2)画流程图时要严格遵循画法规则,符号规范,每一个符号的作用明确,让别人一看就懂. 下列关于流程图的图形符号的理解,正确的有________.
①任何一个流程图都必须有起、止框;
②输入框只能放在开始框后,输出框只能放在结束框前;
③判断框是惟一具有超过一个退出点的图形符号;
④对于一个程序来说,判断框内的条件是惟一的.
【思路点拨】 对叙述逐一分析→判断正误→给出结论.【解析】 根据流程图的概念及图形符号的功能进行判断.任何一个程序都必须有开始和结束,从而必须有起、止框;输入和输出框可以用在算法中任何需要输入、输出的位置;判断框内的条件不是惟一的,如“a>b”也可写成“a≤b”此时其它部分需作相应调整,故正确答案为①③.
【答案】 ①③【名师点评】 深刻理解图形符号的含义及其功能是解决这类问题的关键.自我挑战1 下列有关流程图的叙述中,正确的是________.
?卓越品质源于永不满足—————————————————————————优化方案·成功相伴?①流程图中的图形符号可以由个人来确定;
②输入框可以在起始框后,也可以在判断框后;
③◇可以用来执行计算语句;
④用流程图表达算法的优点是算法的基本逻辑结构展现得非常直接.
解析:流程图中的图形符号是统一规定的;◇用来表示判断框.
答案:②④用顺序结构表示算法(1)顺序结构是由若干个依次执行的步骤组成的,它是任何一个算法都离不开的最简单、最基本的结构.
(2)顺序结构只能解决简单问题,它按从上到下的顺序执行,不含程序步骤的跳转. (本题满分14分)计算下列梯形的面积:上底为3,下底为7,高为6.试设计该问题的算法并画出流程图.
【思路点拨】 利用梯形面积公式直接代入计算即可.【名师点评】 (1)要注意各种图形符号的正确使用.(2)本例的算法及流程图具有代表性,能运用于其他很多套用公式的题目,其步骤是先赋值,再运算,最后输出结果.顺序结构的特征及应用(1)用自然语言表述算法步骤;
(2)确定每一个算法步骤所包含的逻辑结构,并用相应的流程图表示,得到该步骤的流程图;
(3)将所有步骤的流程图用流程线连接起来,并加上起止框,得到表示整个算法的流程图. 如图所示是为解决某个问题而绘制的流程图,仔细分析各图框内的内容及图框之间的关系,回答下面的问题:(1)该流程图解决的是怎样的一个问题?
(2)若最终输出的结果y1=3,y2=-2,当x取5时输出的结果5a+b的值应该是多大?
(3)在(2)的前提下,输入的x值越大,输出的ax+b是不是越大?为什么?
(4)在(2)的前提下,当输入的x值为多大时,输出结果ax+b等于0?
【思路点拨】 仔细阅读每个图框中的信息,并结合对每种图框的功能及意义的理解,从而分析总结出该图框所要解决的问题.【解】 (1)该流程图解决的是求函数f(x)=ax+b的函数值的问题.
(2)y1=3,即2a+b=3,①
y2=-2,即-3a+b=-2,②
由①②得a=1,b=1.∴f(x)=x+1.
∴当x取5时,5a+b=f(5)=5+1=6.
(3)输入的x值越大,输出的函数值ax+b越大,
因为f(x)=x+1是R上的增函数.
(4)令f(x)=x+1=0,得x=-1,
因此当输入的x值为-1时,输出的函数值为0.【名师点评】 本题通过探究流程图中每个图框的意义,使学生加深对流程框图的概念及意义的理解,本题中流程框图是采用的顺序结构,因此,我们可以根据流程线的顺序对图框进行逐个分析.自我挑战2 如图所示的流程图,根据该图和下列各小题的条件回答问题.(1)该流程图解决的是一个什么问题?
(2)当输入的x值为0和4时,输出的值相等,问当输入的x的值为3时,输出的值为多大?
(3)在(2)的前提下,要想使输出的值最大,输入的x的值应为多大?
(4)在(2)的前提下,按照这个流程图,当x值都大于2时,x值大的输出的y值反而小,为什么?
(5)在(2)的前提下,要想使输出的值等于3,输入的x应是多少?
(6)在(2)的前提下,要想使输入的值与输出的值相等,输入的值应是多大?解:(1)流程图解决的是求函数f(x)=-x2+mx的函数值的问题,其中输入的是自变量x的值,输出的是x对应的函数值.
(2)因为x=0或x=4时,y值相等,所以m=4,
所以x=3时,y=-32+4×3=-9+12=3.
(3)y=-x2+4x=-(x-2)2+4,
∴当输入的x值为2时,输出的值最大.
(4)当x>2时,y=-(x-2)2+4为减函数,
所以x增大时,输出的y值反而小.
(5)∵y=-x2+4x=3,∴x=1或3.
(6)∵-x2+4x=x,∴x2-3x=0,∴x=0或x=3.1.(1)流程图的每一种图形符号都有特定的含义,在画流程图时不能混用;
(2)在画流程图前,一般先用自然语言编写算法.
2.顺序结构中强调“依次处理”,“从上到下”依次进行每一步,不能“回头”.
