人教版七年级数学 下册 第八章 8.2 消元—解二元一次方程组 第1课时 代入法 课件(共26张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第八章 8.2 消元—解二元一次方程组 第1课时 代入法 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 497.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 09:28:08 | ||
图片预览







文档简介
(共26张PPT)
《一千零一夜》中有这样一段文字:有一群鸽子,
其中一部分在树上欢歌,另一部分在地上觅食.树
上的一只鸽子对地上觅食的鸽子说:“若从你们中
飞上来1只,则地上的鸽子就是整群鸽子的1;若从
树上飞下去1只.则树上
和地上的鸽子就一样多
了”你知道树上、地上
各有多少只鸽子吗
激情引导
8.2 消元—解二元一次方程组
第1课时 代入法
人教版七年级数学 下册
目标导航
1.掌握代入消元法的意义;
2.会用代入法解二元一次方程组;
3.初步学习列二元一次方程组解应用题.
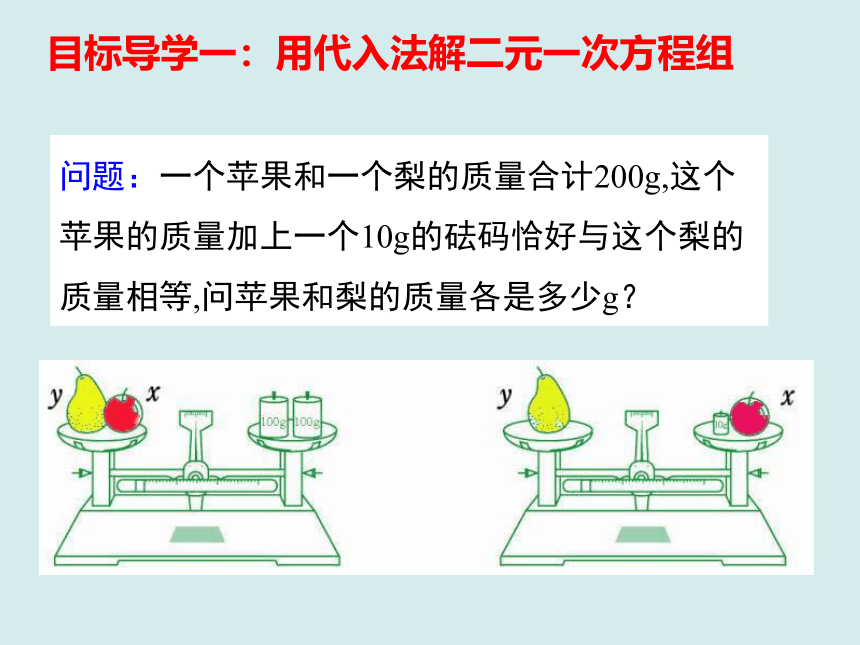
问题:一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
目标导学一:用代入法解二元一次方程组
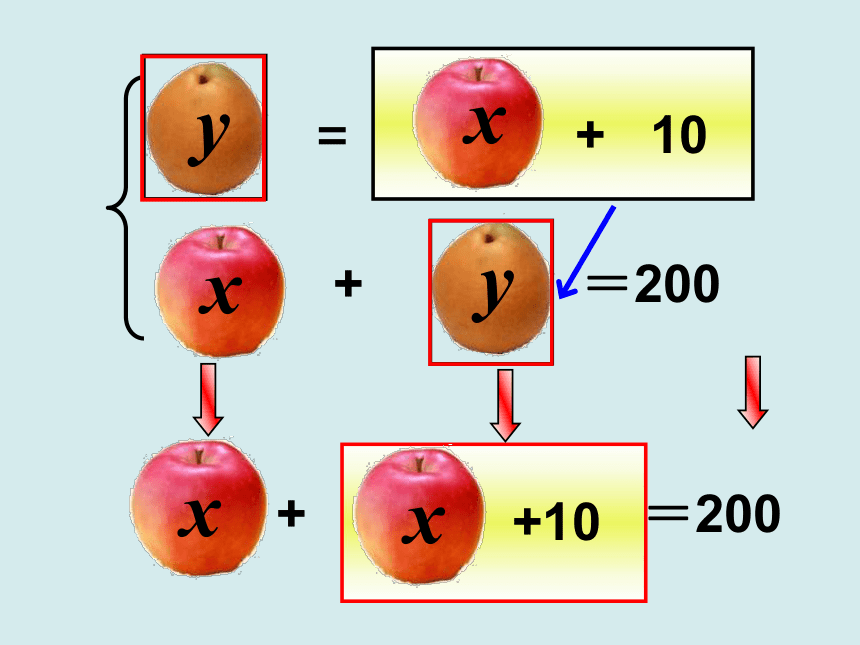
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
例1:体育节要到了,篮球是七年级(1)班的拳头项目.为了取得好名次,他们想在全部22场比赛中得到40分.已知每场比赛都要分出胜负,胜队得2分,负队得1分.那么七年级(1)班应该胜、负各几场
你会用二元一次方程组解决这个问题吗
根据问题中的等量关系,设胜x场,负y场,可以更容易地列出方程:
x+y=22, ①
2x+y=40.②
那么有哪些方法可以求得二元一次方程组的解呢
例1:体育节要到了,篮球是七年级(1)班的拳头项目.为了取得好名次,他们想在全部22场比赛中得到40分.已知每场比赛都要分出胜负,胜队得2分,负队得1分.那么七年级(1)班应该胜、负各几场
你会用二元一次方程组解决这个问题吗
讲解:
由方程①进行移项得y=22-x,
由于方程②中的y与方程①中的y都表示负的场数,
故可以把方程②中的y用22-x来代换,
即得2x+(22-x)=40.则二元化为一元了.
解得x=18.
问题解完了吗 怎样求y
将x=18代入方程y=22-x,
得y=4.
能代入原方程组中的方程①②来求y吗 代入哪个方程更简便
归纳:这种把二元一次方程中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得二元一次方程组的解的方法叫做代入消元法,简称代入法.
x=18,
y=4.
这样,二元一次方程组的解是
例2 用代入法解方程组
解:把①代入②,得
3(y+3)-8y=14,
所以y=-1.
把y=-1代入①,得x=2.
用代入消元法解二元一次方程组的一般步骤及方法:
①变形为y=ax+b(或x=ay+b)的形式;
②代入;
③求出一个未知数;
④求出另一个未知数;
⑤写出解 .
解:由②,得2y=3x-5.③
把③代入①,得4x+4(3x-5)=12,解得x=2.
把x=2代入③,得
所以这个方程组的解是
例3 用代入消元法解方程组:
观察方程组可以发现,两个方程中x与y的系数的
绝对值都不相等,但①中y的系数的绝对值是②
中y的系数的绝对值的4倍,因此可把2y看作一个
整体代入.
1.把下列方程改写成用含x的式子表示y的形式.
(1)2x-y=3; (2)3x+y-1=0.
2.用代入法解下列方程组:
1.(1)y=2x-3;(2)y=1-3x.
答案:
练一练
例4 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
等量关系:
⑴大瓶数
小瓶数
⑵大瓶所装消毒液
小瓶所装消毒液
总生产量.
目标导学二:代入法解二元一次方程组的简单应用
解:设这些消毒液应该分装x大瓶、y小瓶.
根据题意可列方程组:
③
①
由 得:
把 代入 得:
③
②
解得:x=20000
把x=20000代入 得:y=50000
③
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
í
ì
=
+
=
22500000
250
500
2
5
y
x
y
x
归纳总结
2、列方程组解决实际问题时应注意什么?
1、列方程组解应用题的一般步骤:
审:弄清题目中的数量关系
设:设出两个未知数
找:分析题意,找出两个等量关系
列:根据等量关系列出方程组
解:解出方程组,求出未知数的值
检答:检验求得的值是否正确和符合实际情形,
然后作答
1)、弄清题目,找对已知量、未知量之间的等量关系。
2)、单位不统一时需统一单位。
3)、方程两边的量要一致.
例5、王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,用去了44000元,其中种茄子每亩用了1700元,获纯利2400元,种西红柿每亩用了1800元,获纯利2600元,问王大伯一共获纯利多少元
解:设王大析种了x亩茄子,y亩西红柿,根据题意得
解得
所以获纯利为10×2400+15×2600=63000元
1.如图所示,将长方形ABCD的一个角折叠,折痕为AE,∠BAD比∠BAE大48°。设∠BAE和∠BAD的度数分别为x ,y度,那么x,y所适合的一个方程组是( )
A
B
C
D
C
练一练
2.有48支队520名运动员参加篮球、排球比赛,其中每支篮球队10人,每支排球队12人,每名运动员只能参加一项比赛.篮球、排球队各有多少支参赛
解:设篮球队有x支,排球队有y支,由题意,得
答:篮球队有28支,排球队有20支.
练一练
1.二元一次方程组
代入消元法
一元一次方程
2.代入消元法的一般步骤:
3.思想方法:转化思想、消元思想、方程(组)思想.
变
代
求
写
转化
课堂小结
1. 用代入法解方程组 比较合理的变
形是( )
A.由①得
B.由①得
C.由②得
D.由②得y=2x-5
检测目标
2. 用代入法解方程组 较简单的
方法是( )
A.消y B.消x
C.消x和消y一样 D.无法确定
检测目标
3、张翔从学校出发骑自行车去县城,中途因道路施工
步行一段路,1.5 h后到达县城.他骑车的平均速度是
15 km/h,步行的平均速度是5 km/h,路程全长20 km.
他骑车与步行各用多少时间
解:设他骑车用的时间为x h ,则他步行用的时间为(1.5-x) h.根据题意,得15x+5(1.5-x)=20.
解得x=1.25. 则1.5-1.25=0.25( h ).
答:他骑车用了1.25 h ,步行用了0.25 h .
检测目标
通过本课学习,你收获了什么?
《一千零一夜》中有这样一段文字:有一群鸽子,
其中一部分在树上欢歌,另一部分在地上觅食.树
上的一只鸽子对地上觅食的鸽子说:“若从你们中
飞上来1只,则地上的鸽子就是整群鸽子的1;若从
树上飞下去1只.则树上
和地上的鸽子就一样多
了”你知道树上、地上
各有多少只鸽子吗
激情引导
8.2 消元—解二元一次方程组
第1课时 代入法
人教版七年级数学 下册
目标导航
1.掌握代入消元法的意义;
2.会用代入法解二元一次方程组;
3.初步学习列二元一次方程组解应用题.
问题:一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
目标导学一:用代入法解二元一次方程组
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
例1:体育节要到了,篮球是七年级(1)班的拳头项目.为了取得好名次,他们想在全部22场比赛中得到40分.已知每场比赛都要分出胜负,胜队得2分,负队得1分.那么七年级(1)班应该胜、负各几场
你会用二元一次方程组解决这个问题吗
根据问题中的等量关系,设胜x场,负y场,可以更容易地列出方程:
x+y=22, ①
2x+y=40.②
那么有哪些方法可以求得二元一次方程组的解呢
例1:体育节要到了,篮球是七年级(1)班的拳头项目.为了取得好名次,他们想在全部22场比赛中得到40分.已知每场比赛都要分出胜负,胜队得2分,负队得1分.那么七年级(1)班应该胜、负各几场
你会用二元一次方程组解决这个问题吗
讲解:
由方程①进行移项得y=22-x,
由于方程②中的y与方程①中的y都表示负的场数,
故可以把方程②中的y用22-x来代换,
即得2x+(22-x)=40.则二元化为一元了.
解得x=18.
问题解完了吗 怎样求y
将x=18代入方程y=22-x,
得y=4.
能代入原方程组中的方程①②来求y吗 代入哪个方程更简便
归纳:这种把二元一次方程中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得二元一次方程组的解的方法叫做代入消元法,简称代入法.
x=18,
y=4.
这样,二元一次方程组的解是
例2 用代入法解方程组
解:把①代入②,得
3(y+3)-8y=14,
所以y=-1.
把y=-1代入①,得x=2.
用代入消元法解二元一次方程组的一般步骤及方法:
①变形为y=ax+b(或x=ay+b)的形式;
②代入;
③求出一个未知数;
④求出另一个未知数;
⑤写出解 .
解:由②,得2y=3x-5.③
把③代入①,得4x+4(3x-5)=12,解得x=2.
把x=2代入③,得
所以这个方程组的解是
例3 用代入消元法解方程组:
观察方程组可以发现,两个方程中x与y的系数的
绝对值都不相等,但①中y的系数的绝对值是②
中y的系数的绝对值的4倍,因此可把2y看作一个
整体代入.
1.把下列方程改写成用含x的式子表示y的形式.
(1)2x-y=3; (2)3x+y-1=0.
2.用代入法解下列方程组:
1.(1)y=2x-3;(2)y=1-3x.
答案:
练一练
例4 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
等量关系:
⑴大瓶数
小瓶数
⑵大瓶所装消毒液
小瓶所装消毒液
总生产量.
目标导学二:代入法解二元一次方程组的简单应用
解:设这些消毒液应该分装x大瓶、y小瓶.
根据题意可列方程组:
③
①
由 得:
把 代入 得:
③
②
解得:x=20000
把x=20000代入 得:y=50000
③
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
í
ì
=
+
=
22500000
250
500
2
5
y
x
y
x
归纳总结
2、列方程组解决实际问题时应注意什么?
1、列方程组解应用题的一般步骤:
审:弄清题目中的数量关系
设:设出两个未知数
找:分析题意,找出两个等量关系
列:根据等量关系列出方程组
解:解出方程组,求出未知数的值
检答:检验求得的值是否正确和符合实际情形,
然后作答
1)、弄清题目,找对已知量、未知量之间的等量关系。
2)、单位不统一时需统一单位。
3)、方程两边的量要一致.
例5、王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,用去了44000元,其中种茄子每亩用了1700元,获纯利2400元,种西红柿每亩用了1800元,获纯利2600元,问王大伯一共获纯利多少元
解:设王大析种了x亩茄子,y亩西红柿,根据题意得
解得
所以获纯利为10×2400+15×2600=63000元
1.如图所示,将长方形ABCD的一个角折叠,折痕为AE,∠BAD比∠BAE大48°。设∠BAE和∠BAD的度数分别为x ,y度,那么x,y所适合的一个方程组是( )
A
B
C
D
C
练一练
2.有48支队520名运动员参加篮球、排球比赛,其中每支篮球队10人,每支排球队12人,每名运动员只能参加一项比赛.篮球、排球队各有多少支参赛
解:设篮球队有x支,排球队有y支,由题意,得
答:篮球队有28支,排球队有20支.
练一练
1.二元一次方程组
代入消元法
一元一次方程
2.代入消元法的一般步骤:
3.思想方法:转化思想、消元思想、方程(组)思想.
变
代
求
写
转化
课堂小结
1. 用代入法解方程组 比较合理的变
形是( )
A.由①得
B.由①得
C.由②得
D.由②得y=2x-5
检测目标
2. 用代入法解方程组 较简单的
方法是( )
A.消y B.消x
C.消x和消y一样 D.无法确定
检测目标
3、张翔从学校出发骑自行车去县城,中途因道路施工
步行一段路,1.5 h后到达县城.他骑车的平均速度是
15 km/h,步行的平均速度是5 km/h,路程全长20 km.
他骑车与步行各用多少时间
解:设他骑车用的时间为x h ,则他步行用的时间为(1.5-x) h.根据题意,得15x+5(1.5-x)=20.
解得x=1.25. 则1.5-1.25=0.25( h ).
答:他骑车用了1.25 h ,步行用了0.25 h .
检测目标
通过本课学习,你收获了什么?
