人教版七年级数学 下册 第八章 8.3 实际问题与二元一次方程组 课件(共24张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第八章 8.3 实际问题与二元一次方程组 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
星期天,我们一家6个人去东郊公园看了灯光秀,买门票花了100元。
哦,那你们家去了几个大人?几个小孩呢?
聪明的同学们,你能帮他算算吗?
你太不聪明了,自已不会算吗?成人票每人20元,小孩票每人10元啊!
情境导入
8.3 实际问题与二元一次方程组
人教版七年级数学 下册
目标导航
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.(重点)
2.学会利用二元一次方程组解决几何、行程问题.(重点、难点)
用方程法解决实际问题的步骤:
(1)______ (2)______
(3)______ (4)___ __
(5)______ (6)______
审题
设未知数
列方程
解方程
检验
答
知识回顾
问题引入
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李
大叔估计的准确吗?
目标导学一:列方程组解决实际问题
合作与交流
问题1 题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2 题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用
饲料为xkg和ykg,
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组:x= ,
y= .
20
5
剧情发展:随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人,则:
+ = 42,
+ = 20.
8x
5y
4x
2y
解得:
x =4
y = 2
答:李大叔应聘请甲种饲养员4人,乙种饲养员2人.
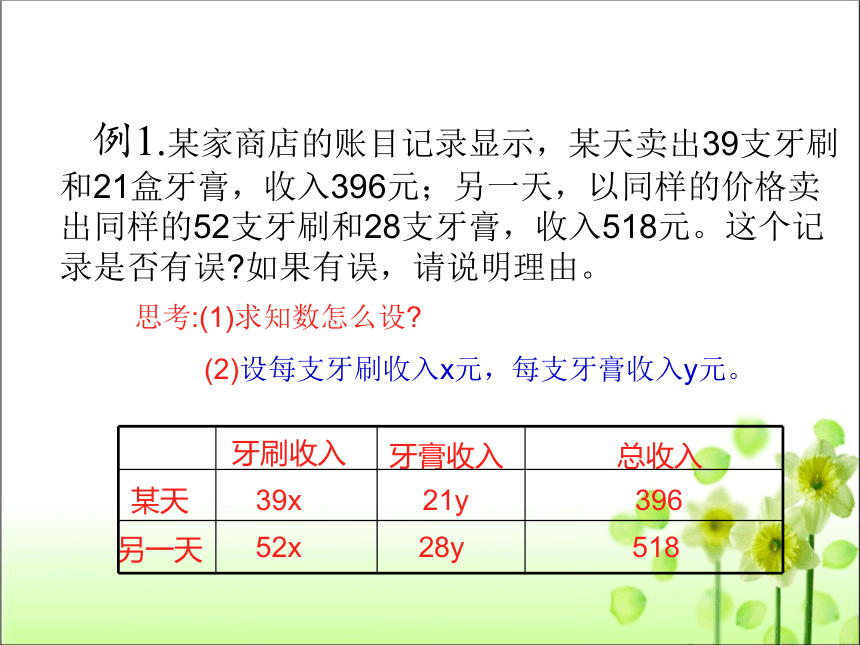
例1.某家商店的账目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28支牙膏,收入518元。这个记录是否有误 如果有误,请说明理由。
牙膏收入
另一天
某天
总收入
牙刷收入
21y
39x
396
52x
28y
518
(2)设每支牙刷收入x元,每支牙膏收入y元。
思考:(1)求知数怎么设
解:设一支牙刷x元,一盒牙膏y元,根据题意得
39x+21y=396 ①
52x+28y=518 ②
①÷3得 13x+7y=132 ③
②÷4得 13x+7y=129.5 ④
∵ 13:13=7:7≠132:129.5
∴ 此方程组无解
所以这个记录是错误的。
例2.某食品厂要配制含蛋白质15%的食品100kg,现在有含蛋白质分别为20%,12%的两种配料. 用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克?
解:设需含蛋白质为20%、12%的配料分别为xkg、ykg, 根据题意列出方程组得
解得
答:需含蛋白质为20%、12%的配料分别为37.5kg、
62.5kg
例3. A、B两地相距80千米,一艘船从A地出发顺水航行4小时到达B地,而从B地逆水航行5小时到达A地,已知船顺水航行、逆水航行的速度分别为船在静水中的速度与水流速度的和与差,求船在静水中的速度和水流的速度。
设船在静水中的速度和在水流中的速度分别为x千米/小时和y千米/小时。
解:
根据题意,得
解得
答:船在静水中的速度和在水流中的速度分别为18千米/小时和2千米/小时。
随堂练习
例4.8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位cm)
60
x+y=60
x=3y
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
目标导学二:列方程组解决几何问题
例5:据以往的统计资料,甲、乙两种作物的单位面积产量的比
是 1:1.5,现要在一块长200m,宽100m的长方形土地上种
植这两种作物,怎样把这块地分为两个长方形,使甲、乙
两种作物的总产量的比是 3 : 4 (结果取整数)
A
B
C
D
甲种作物的总产量 = 甲的单位面积产量×甲的种植面积
乙种作物的总产量 = 乙的单位面积产量 ×乙的种植面积
思考:
1、“甲、乙两种作物的单位面积产量的比是1:1.5”是什么意思?
2、“甲、乙两种作物的总产量的比是3:4”是什么意思?
3、本题中有哪些相等关系?
解:设AE为 x 米,BE为 y 米,由题意得:
x + y=200
100 x: 1.5×100 y =3:4
A
B
C
D
●
E
┓
x
y
解方程组得:
x=
y =
由题意取值:
X≈ 106
y ≈ 94
答: 过长方形土地的长边上离一端约106米处,
把这块地分为两个长方形.较大一块地种甲种作
物,较小一块地种乙种作物.
A
B
C
D
●
E
┓
y
x
解:设CE为 x 米,BE为 y 米,由题意得:
x + y=100
200 x: 1.5×200 y =3:4
解方程组得:
x=
y =
由题意取值:
X≈ 53
y ≈ 47
答: 过长方形土地的短边上离一端约53米处,
把这块地分为两个长方形.较大一块地种甲
种作物,较小一块地种乙种作物.
一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽。
解:设长方形的长为xcm,宽为ycm,
由题意得:
X-4
4
y
2
Ⅰ
Ⅱ
拓展练习:
解得
答:原长方形的长8cm,宽2cm.
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
课堂小结
1.一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为 ( )
A、X=3,y=2 B、x=14,y=1 C、x=15,y=1 D、x=14,y=2
B
检测目标
2.有甲、乙两数,甲数的3倍与乙数的2倍之和等于47,甲数的5倍比乙数的6倍小1,这两个数分别是多少?
解得
答:甲数为10,乙数为 .
检测目标
解:
设甲、乙运动员的速度分别为xm/s,ym/s。
根据等量关系,得
解此方程组,得
答:甲、乙运动员的速度分别为6m/s,4m/s。
典型例题
3.育才中学新建塑胶操场跑道周长为400m,甲、乙两名运动员从同一起点同时出发,相背而跑,40s后首次相遇,若从同一起点同向而跑,200s后甲首次追上乙,求甲、乙运动员的速度。
通过本课学习,你收获了什么?
星期天,我们一家6个人去东郊公园看了灯光秀,买门票花了100元。
哦,那你们家去了几个大人?几个小孩呢?
聪明的同学们,你能帮他算算吗?
你太不聪明了,自已不会算吗?成人票每人20元,小孩票每人10元啊!
情境导入
8.3 实际问题与二元一次方程组
人教版七年级数学 下册
目标导航
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.(重点)
2.学会利用二元一次方程组解决几何、行程问题.(重点、难点)
用方程法解决实际问题的步骤:
(1)______ (2)______
(3)______ (4)___ __
(5)______ (6)______
审题
设未知数
列方程
解方程
检验
答
知识回顾
问题引入
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李
大叔估计的准确吗?
目标导学一:列方程组解决实际问题
合作与交流
问题1 题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2 题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用
饲料为xkg和ykg,
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组:x= ,
y= .
20
5
剧情发展:随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人,则:
+ = 42,
+ = 20.
8x
5y
4x
2y
解得:
x =4
y = 2
答:李大叔应聘请甲种饲养员4人,乙种饲养员2人.
例1.某家商店的账目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28支牙膏,收入518元。这个记录是否有误 如果有误,请说明理由。
牙膏收入
另一天
某天
总收入
牙刷收入
21y
39x
396
52x
28y
518
(2)设每支牙刷收入x元,每支牙膏收入y元。
思考:(1)求知数怎么设
解:设一支牙刷x元,一盒牙膏y元,根据题意得
39x+21y=396 ①
52x+28y=518 ②
①÷3得 13x+7y=132 ③
②÷4得 13x+7y=129.5 ④
∵ 13:13=7:7≠132:129.5
∴ 此方程组无解
所以这个记录是错误的。
例2.某食品厂要配制含蛋白质15%的食品100kg,现在有含蛋白质分别为20%,12%的两种配料. 用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克?
解:设需含蛋白质为20%、12%的配料分别为xkg、ykg, 根据题意列出方程组得
解得
答:需含蛋白质为20%、12%的配料分别为37.5kg、
62.5kg
例3. A、B两地相距80千米,一艘船从A地出发顺水航行4小时到达B地,而从B地逆水航行5小时到达A地,已知船顺水航行、逆水航行的速度分别为船在静水中的速度与水流速度的和与差,求船在静水中的速度和水流的速度。
设船在静水中的速度和在水流中的速度分别为x千米/小时和y千米/小时。
解:
根据题意,得
解得
答:船在静水中的速度和在水流中的速度分别为18千米/小时和2千米/小时。
随堂练习
例4.8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位cm)
60
x+y=60
x=3y
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
目标导学二:列方程组解决几何问题
例5:据以往的统计资料,甲、乙两种作物的单位面积产量的比
是 1:1.5,现要在一块长200m,宽100m的长方形土地上种
植这两种作物,怎样把这块地分为两个长方形,使甲、乙
两种作物的总产量的比是 3 : 4 (结果取整数)
A
B
C
D
甲种作物的总产量 = 甲的单位面积产量×甲的种植面积
乙种作物的总产量 = 乙的单位面积产量 ×乙的种植面积
思考:
1、“甲、乙两种作物的单位面积产量的比是1:1.5”是什么意思?
2、“甲、乙两种作物的总产量的比是3:4”是什么意思?
3、本题中有哪些相等关系?
解:设AE为 x 米,BE为 y 米,由题意得:
x + y=200
100 x: 1.5×100 y =3:4
A
B
C
D
●
E
┓
x
y
解方程组得:
x=
y =
由题意取值:
X≈ 106
y ≈ 94
答: 过长方形土地的长边上离一端约106米处,
把这块地分为两个长方形.较大一块地种甲种作
物,较小一块地种乙种作物.
A
B
C
D
●
E
┓
y
x
解:设CE为 x 米,BE为 y 米,由题意得:
x + y=100
200 x: 1.5×200 y =3:4
解方程组得:
x=
y =
由题意取值:
X≈ 53
y ≈ 47
答: 过长方形土地的短边上离一端约53米处,
把这块地分为两个长方形.较大一块地种甲
种作物,较小一块地种乙种作物.
一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽。
解:设长方形的长为xcm,宽为ycm,
由题意得:
X-4
4
y
2
Ⅰ
Ⅱ
拓展练习:
解得
答:原长方形的长8cm,宽2cm.
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
课堂小结
1.一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为 ( )
A、X=3,y=2 B、x=14,y=1 C、x=15,y=1 D、x=14,y=2
B
检测目标
2.有甲、乙两数,甲数的3倍与乙数的2倍之和等于47,甲数的5倍比乙数的6倍小1,这两个数分别是多少?
解得
答:甲数为10,乙数为 .
检测目标
解:
设甲、乙运动员的速度分别为xm/s,ym/s。
根据等量关系,得
解此方程组,得
答:甲、乙运动员的速度分别为6m/s,4m/s。
典型例题
3.育才中学新建塑胶操场跑道周长为400m,甲、乙两名运动员从同一起点同时出发,相背而跑,40s后首次相遇,若从同一起点同向而跑,200s后甲首次追上乙,求甲、乙运动员的速度。
通过本课学习,你收获了什么?
