华师大版 八年级上册 11.1.2立方根 课件(共34张PPT)
文档属性
| 名称 | 华师大版 八年级上册 11.1.2立方根 课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 09:49:33 | ||
图片预览










文档简介
(共34张PPT)
11.1 平方根与立方根
第11章 数的开方
11.1.2 立方根
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
立方根
立方根的性质
用计算器求一个数的立方根
知识点
立方根
知1-讲
感悟新知
1
1. 定义 如果一个数的立方等于a,那么这个数叫做a 的立方根.
表示方法:一个数a 的立方根,用符号“ ”表示,
读作“三次根号a”,其中a 是被开方数,3 是根指数.
特别警示: 中的根指数3 不能省略. 若省略了3,
表示非负数a 的算术平方根而非a 的立方根.
知1-讲
感悟新知
2. 开立方 求一个数的立方根的运算,叫做开立方.
特别解读:立方根与开立方的关系:立方根是一个数,是开立方的结果;而开立方是求一个数的立方根的运算.
知1-讲
感悟新知
特别提醒
立方根与平方根的区别:
1. 被开方数:前者可为任何数,后者为非负数;
2. 根指数:前者不能省略,后者可省略不写;
3. 个数:立方根只有一个,平方根有两个(特殊情况:0 的平方根是0).
感悟新知
知1-练
求下列各数的立方根:
(1)-125;(2)2 ;(3)-1.
例 1
解题秘方:根据立方根的定义,用立方法求解.
感悟新知
知1-练
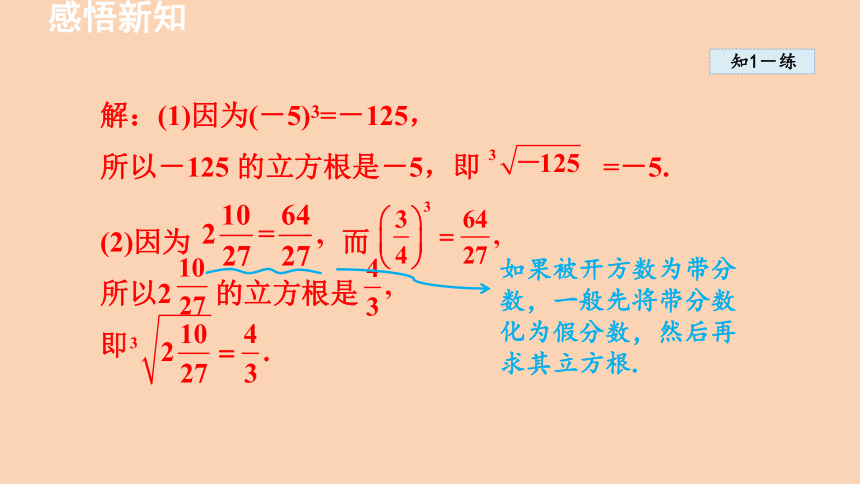
解:(1)因为(-5)3=-125,
所以-125 的立方根是-5,即 =-5.
(2)因为 而
所以2 的立方根是
即
如果被开方数为带分
数,一般先将带分数
化为假分数,然后再
求其立方根.
感悟新知
知1-练
(3)因为(-1)3=-1,
所以-1的立方根是-1,即 =-1.
感悟新知
知1-练
1-1. 求下列各数的立方根
(1)-27;
解:因为(-3)3=-27,所以-27的立方根是-3.
感悟新知
知1-练
(3)0.216;
(4)-5;
解:因为0.63=0.216,所以0.216的立方根是0.6.
感悟新知
知1-练
已知x-2 的平方根是±2,2x+y+7 的立方根是3,求x2+y2 的算术平方根.
解题秘方:一个数等于它的平方根的平方,等于它的立方根的立方.
例2
感悟新知
知1-练
解:因为x-2 的平方根是±2,所以x-2=4.
所以x=6.
因为2x+y+7 的立方根是3,所以2x+y+7=27.
把x=6 代入2x+y+7=27,解得y=8,
所以x2+y2=62+82=100. 所以x2+y2 的算术平方根为10.
感悟新知
知1-练
2-1. 已知一个正数的两个平方根分别是a-3 和a-11,a+2b-3 的立方根是2,求2a+b 的算术平方根.
感悟新知
知1-练
知识点
立方根的性质
知2-讲
感悟新知
2
1.性质
特别提醒
●立方根是它本身的数只有0 和±1.
●互为相反数的两个数,它们的立方根也互为相反数,即 .利用“ ”可以把求一个负数的立方根转化为求一个正数的立方根的相反数.
●
知2-讲
感悟新知
(1)正数的立方根是正数;
(2)负数的立方根是负数;
(3)0 的立方根是0;
(4)
(5)
知2-讲
感悟新知
2. 平方根与立方根的比较
名称
关系 平方根 立方根
区别 定义 如果一个数的平方等于a,那么这个数叫做a 的平方根 如果一个数的立方等于a,那么这个数叫做a 的立方根
性质 正数有两个平方根,它们互为相反数 正数有一个立方根,仍为正数
负数没有平方根 负数有一个立方根,仍为负数
表示法 ± (a≥0) (a 为任意数)
知2-讲
感悟新知
联系 ①开平方与开立方都与相应的乘方运算互为逆运算
② 0 的平方根和立方根都是0
感悟新知
知2-练
求下列各式的值:
例 3
解题秘方:根据立方根和平方根的性质进行化简计算.
感悟新知
知2-练
感悟新知
知2-练
3-1. 求下列各式的值:
感悟新知
知2-练
感悟新知
知2-练
已知 和 互为相反数,且x ≠ 0,y ≠ 0,求 的值.
解题秘方:根据立方根互为相反数,则被开方数互为相反数,建立x 与y 之间的等量关系求解.
例4
感悟新知
知2-练
解:因为 和 互为相反数,
所以3y-1 和1-2x 互为相反数,
即(3y-1)+(1-2x)=0,化简得3y=2x.
又因为x ≠ 0,y ≠ 0,所以
感悟新知
知2-练
4-1. 若 与 互为相反数, 求 的值.
知识点
用计算器求一个数的立方根
知3-讲
感悟新知
3
用计算器求一个数的立方根和求一个数的算术平方根的步骤相同,只是按的根指数键不同.
步骤:按键 → 被开方数 → → 根据显示结果写出立方根. 或者按键 → 被开方数 → →根据显示结果写出立方根.
知3-讲
感悟新知
特别警示
不同型号的计算器按键的顺序可能不同,使用计算器时,一定要按说明书操作.
感悟新知
知3-练
用计算器求下列各数的立方根:
(1)64;(2)100( 精确到0.01);(3)-13.27(精确到0.001).
解题秘方:根据计算器求立方根的步骤进行按键操作.
例 5
感悟新知
知3-练
解:(1)依次按键 ,显示:4.
所以 =4.
(2)依次按键 ,显示:4.641 588 834.所以 ≈ 4.64.
(3)依次按键 ,显示:2.367 501 744.所以 ≈ 2.368. 所以 ≈ -2.368.
感悟新知
知3-练
B
5-1. 已知 ≈0.669 4, ≈ 1.442, 那么下列各式中正确的是( )
A. ≈ 14.42
B. ≈ 6.694
C. ≈ 144.2
D. ≈ 66.94
感悟新知
知3-练
比较下列各组数的大小:
解题秘方:可以用计算器求出各个数的近似数进行比较,也可以借助中间值进行比较.
例6
(2)(计算器求值法)因为 ≈ 3.476>3.4,
所以- <-3.4.
感悟新知
知3-练
解:(1)(中间值法)因为2= < ,2= > ,
所以 > .
(3)(立方法)因为( )3=6,23=8,6<8,所以 <2.
感悟新知
知3-练
6-1. 比较下列各组数的大小:
课堂小结
立方根
立方根
定义
性质
正数的立方根是正数
0的立方根是0
负数的立方根是负数
11.1 平方根与立方根
第11章 数的开方
11.1.2 立方根
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
立方根
立方根的性质
用计算器求一个数的立方根
知识点
立方根
知1-讲
感悟新知
1
1. 定义 如果一个数的立方等于a,那么这个数叫做a 的立方根.
表示方法:一个数a 的立方根,用符号“ ”表示,
读作“三次根号a”,其中a 是被开方数,3 是根指数.
特别警示: 中的根指数3 不能省略. 若省略了3,
表示非负数a 的算术平方根而非a 的立方根.
知1-讲
感悟新知
2. 开立方 求一个数的立方根的运算,叫做开立方.
特别解读:立方根与开立方的关系:立方根是一个数,是开立方的结果;而开立方是求一个数的立方根的运算.
知1-讲
感悟新知
特别提醒
立方根与平方根的区别:
1. 被开方数:前者可为任何数,后者为非负数;
2. 根指数:前者不能省略,后者可省略不写;
3. 个数:立方根只有一个,平方根有两个(特殊情况:0 的平方根是0).
感悟新知
知1-练
求下列各数的立方根:
(1)-125;(2)2 ;(3)-1.
例 1
解题秘方:根据立方根的定义,用立方法求解.
感悟新知
知1-练
解:(1)因为(-5)3=-125,
所以-125 的立方根是-5,即 =-5.
(2)因为 而
所以2 的立方根是
即
如果被开方数为带分
数,一般先将带分数
化为假分数,然后再
求其立方根.
感悟新知
知1-练
(3)因为(-1)3=-1,
所以-1的立方根是-1,即 =-1.
感悟新知
知1-练
1-1. 求下列各数的立方根
(1)-27;
解:因为(-3)3=-27,所以-27的立方根是-3.
感悟新知
知1-练
(3)0.216;
(4)-5;
解:因为0.63=0.216,所以0.216的立方根是0.6.
感悟新知
知1-练
已知x-2 的平方根是±2,2x+y+7 的立方根是3,求x2+y2 的算术平方根.
解题秘方:一个数等于它的平方根的平方,等于它的立方根的立方.
例2
感悟新知
知1-练
解:因为x-2 的平方根是±2,所以x-2=4.
所以x=6.
因为2x+y+7 的立方根是3,所以2x+y+7=27.
把x=6 代入2x+y+7=27,解得y=8,
所以x2+y2=62+82=100. 所以x2+y2 的算术平方根为10.
感悟新知
知1-练
2-1. 已知一个正数的两个平方根分别是a-3 和a-11,a+2b-3 的立方根是2,求2a+b 的算术平方根.
感悟新知
知1-练
知识点
立方根的性质
知2-讲
感悟新知
2
1.性质
特别提醒
●立方根是它本身的数只有0 和±1.
●互为相反数的两个数,它们的立方根也互为相反数,即 .利用“ ”可以把求一个负数的立方根转化为求一个正数的立方根的相反数.
●
知2-讲
感悟新知
(1)正数的立方根是正数;
(2)负数的立方根是负数;
(3)0 的立方根是0;
(4)
(5)
知2-讲
感悟新知
2. 平方根与立方根的比较
名称
关系 平方根 立方根
区别 定义 如果一个数的平方等于a,那么这个数叫做a 的平方根 如果一个数的立方等于a,那么这个数叫做a 的立方根
性质 正数有两个平方根,它们互为相反数 正数有一个立方根,仍为正数
负数没有平方根 负数有一个立方根,仍为负数
表示法 ± (a≥0) (a 为任意数)
知2-讲
感悟新知
联系 ①开平方与开立方都与相应的乘方运算互为逆运算
② 0 的平方根和立方根都是0
感悟新知
知2-练
求下列各式的值:
例 3
解题秘方:根据立方根和平方根的性质进行化简计算.
感悟新知
知2-练
感悟新知
知2-练
3-1. 求下列各式的值:
感悟新知
知2-练
感悟新知
知2-练
已知 和 互为相反数,且x ≠ 0,y ≠ 0,求 的值.
解题秘方:根据立方根互为相反数,则被开方数互为相反数,建立x 与y 之间的等量关系求解.
例4
感悟新知
知2-练
解:因为 和 互为相反数,
所以3y-1 和1-2x 互为相反数,
即(3y-1)+(1-2x)=0,化简得3y=2x.
又因为x ≠ 0,y ≠ 0,所以
感悟新知
知2-练
4-1. 若 与 互为相反数, 求 的值.
知识点
用计算器求一个数的立方根
知3-讲
感悟新知
3
用计算器求一个数的立方根和求一个数的算术平方根的步骤相同,只是按的根指数键不同.
步骤:按键 → 被开方数 → → 根据显示结果写出立方根. 或者按键 → 被开方数 → →根据显示结果写出立方根.
知3-讲
感悟新知
特别警示
不同型号的计算器按键的顺序可能不同,使用计算器时,一定要按说明书操作.
感悟新知
知3-练
用计算器求下列各数的立方根:
(1)64;(2)100( 精确到0.01);(3)-13.27(精确到0.001).
解题秘方:根据计算器求立方根的步骤进行按键操作.
例 5
感悟新知
知3-练
解:(1)依次按键 ,显示:4.
所以 =4.
(2)依次按键 ,显示:4.641 588 834.所以 ≈ 4.64.
(3)依次按键 ,显示:2.367 501 744.所以 ≈ 2.368. 所以 ≈ -2.368.
感悟新知
知3-练
B
5-1. 已知 ≈0.669 4, ≈ 1.442, 那么下列各式中正确的是( )
A. ≈ 14.42
B. ≈ 6.694
C. ≈ 144.2
D. ≈ 66.94
感悟新知
知3-练
比较下列各组数的大小:
解题秘方:可以用计算器求出各个数的近似数进行比较,也可以借助中间值进行比较.
例6
(2)(计算器求值法)因为 ≈ 3.476>3.4,
所以- <-3.4.
感悟新知
知3-练
解:(1)(中间值法)因为2= < ,2= > ,
所以 > .
(3)(立方法)因为( )3=6,23=8,6<8,所以 <2.
感悟新知
知3-练
6-1. 比较下列各组数的大小:
课堂小结
立方根
立方根
定义
性质
正数的立方根是正数
0的立方根是0
负数的立方根是负数
