华师大版 八年级上册 12.3乘法公式 课件(共32张PPT)
文档属性
| 名称 | 华师大版 八年级上册 12.3乘法公式 课件(共32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 09:54:46 | ||
图片预览







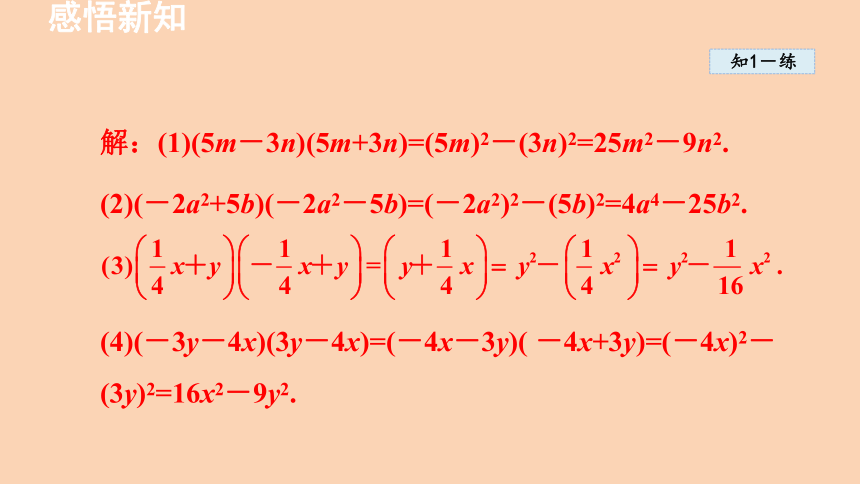
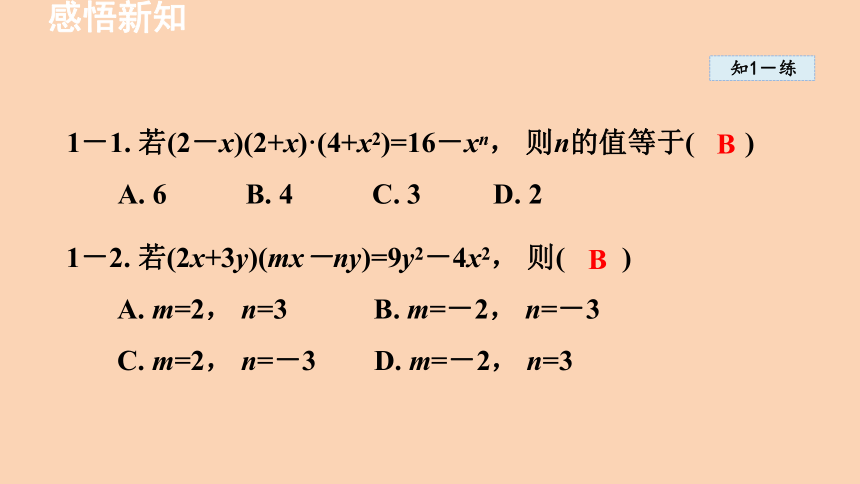
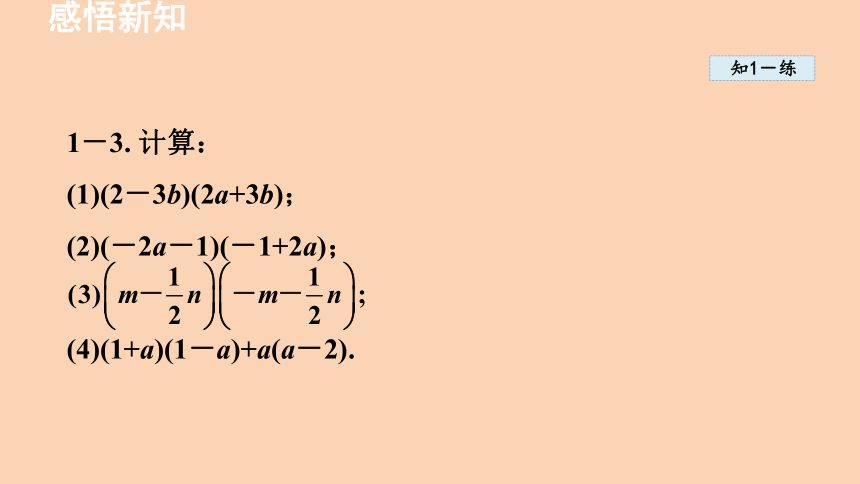
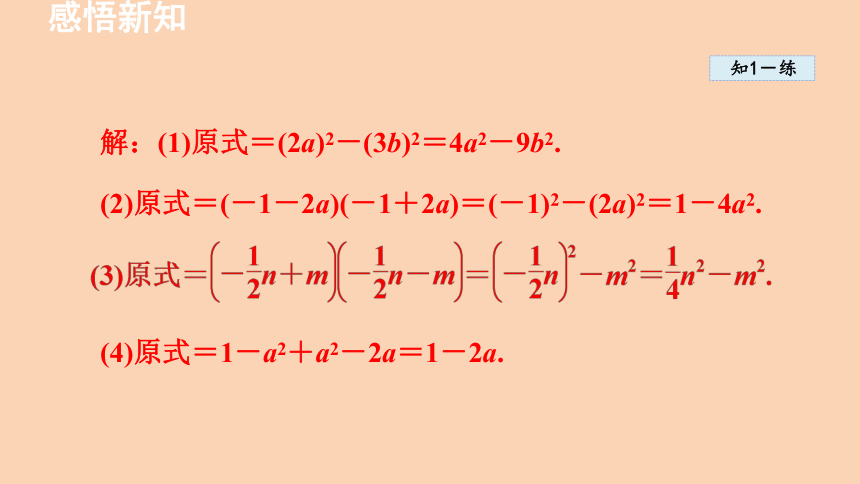

文档简介
(共32张PPT)
12.3 乘法公式
第12章 整数的乘除
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
两数和乘以这两数的差
两数和(差)的平方公式
知识点
两数和乘以这两数的差
知1-讲
感悟新知
1
1. 平方差公式 两数和与这两数差的积,等于这两数的平方差,这个公式叫做两数和与这两数差的乘法公式,有时也简称为平方差公式.
即:用字母表示为(a+b)(a-b)=a2-b2.
知1-讲
感悟新知
特别解读
公式的特征:
1. 等号左边是两个二项式相乘,这两个二项式中有一项完全相同,另一项互为相反数;
2. 等号右边是乘式中两项的平方差,即相同项的平方减去相反项的平方;
3. 理解字母a、b的意义,平方差公式中的a、b既可代表一个单项式,也可代表一个多项式.
知1-讲
感悟新知
2. 平方差公式的几种常见变化及应用
变化形式 应用举例
位置变化 (b+a)(-b+a)=(a+b)(a-b)=a2-b2
符号变化 (-a-b)(a-b)=(-b-a)(-b+a)=(-b)2-a2=b2-a2
系数变化 (3a+2b)(3a-2b)=(3a)2-(2b)2 =9a2-4b2
指数变化 (a3+b2)(a3-b2)=(a3)2-(b2)2 =a6-b4
增项变化 (a-b+c)(a-b-c)=(a-b)2-c2
连用公式 (a+b)(a-b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4
感悟新知
知1-练
计算:
(1)(5m-3n)(5m+3n);(2)(-2a2+5b)(-2a2-5b);
(3) (4)(-3y-4x)(3y-4x).
例 1
解题秘方:先确定公式中的“a”和“b”,然后根据平方差公式(a+b)(a-b)=a2-b2 进行计算.
感悟新知
知1-练
解法提醒:运用平方差公式计算的三个关键步骤:
第1 步,利用加法的交换律调整两个二项式中项的位置,使之与公式左边相对应,已对应的就不需调整,如(1)(2)不需调整,(3)(4)就必须调整.
第2步,找准公式中的a、b 分别代表哪个单项式或多项式.
第3 步,套用公式计算,注意将底数带上括号. 如(1)中(5m)2不能写成5m2.
感悟新知
知1-练
解:(1)(5m-3n)(5m+3n)=(5m)2-(3n)2=25m2-9n2.
(2)(-2a2+5b)(-2a2-5b)=(-2a2)2-(5b)2=4a4-25b2.
(4)(-3y-4x)(3y-4x)=(-4x-3y)( -4x+3y)=(-4x)2-(3y)2=16x2-9y2.
感悟新知
知1-练
1-1. 若(2-x)(2+x)·(4+x2)=16-xn, 则n的值等于( )
A. 6 B. 4 C. 3 D. 2
1-2. 若(2x+3y)(mx-ny)=9y2-4x2, 则( )
A. m=2, n=3 B. m=-2, n=-3
C. m=2, n=-3 D. m=-2, n=3
B
B
感悟新知
知1-练
1-3. 计算:
(1)(2-3b)(2a+3b);
(2)(-2a-1)(-1+2a);
(4)(1+a)(1-a)+a(a-2).
感悟新知
知1-练
解:(1)原式=(2a)2-(3b)2=4a2-9b2.
(2)原式=(-1-2a)(-1+2a)=(-1)2-(2a)2=1-4a2.
(4)原式=1-a2+a2-2a=1-2a.
感悟新知
知1-练
计算:
(1)10.3×9.7;(2)2 022×2 024-2 0232.
解题秘方:找出平方差公式的模型,利用平方差公式进行计算.
例2
感悟新知
知1-练
解:(1)10.3×9.7
=(10+0.3)×(10-0.3)
=102-0.32
=100-0.09
=99.91.
10.3与9.7的平均数为10.
感悟新知
知1-练
(2)2 022×2 024-2 0232
=(2 023-1)×(2 023+1) -2 0232
=2 0232-1-2 0232
=-1.
2022与2024的平均数为2023.
感悟新知
知1-练
2-1. 运用平方差公式进行简便计算:
(1)9.8×10.2;
(2)1 007×993;
(3)129×127-1282.
感悟新知
知1-练
解:(1)原式=(10-0.2)×(10+0.2)=102-0.22=100-0.04=99.96.
(2)原式=(1 000+7)×(1 000-7)=1 0002-72=1 000 000-49=999 951.
(3)原式=(128+1)×(128-1)-1282=1282-12-1282=-1.
知识点
两数和(差)的平方公式
知2-讲
感悟新知
2
1. 两数和(差)的平方公式(也称完全平方公式) 两数和(差)的平方,等于这两数的平方和加上(减去)它们的积的2 倍.
即: 用字母表示为(a+b)2=a2+2ab+b2,(a-b)2=
a2-2ab+b2.
知2-讲
感悟新知
2. 两数和(差)的平方公式的几种常见变形公式
(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab;
(2)(a+b)2=(a-b)2 +4ab;
(3)(a-b)2=(a+b)2-4ab;
(4)(a+b)2+(a-b)2=2(a2+b2);
(5)(a+b)2 - (a-b)2 =4ab;
知2-讲
感悟新知
(6)ab= [(a+b)2-(a2+b2)]= [(a+b)2-(a-b)2];
(7)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(8)a2+b2+c2+ab+ac+bc= [(a+b)2+(b+c)2+(a+c)2 ]
知2-讲
感悟新知
特别解读
1. 弄清公式的特征:公式的左边是一个二项式的平方,公式的右边是一个三项式,包括左边二项式的各项的平方和,另一项是这两项的乘积的2 倍.
2. 理解字母a、b 的意义:公式中的字母a、b 可以表示具体的数,也可以表示含字母的单项式或多项式.
感悟新知
知2-练
计算:
(1)(x+7y)2; (2)(-4a+5b)2;
(3)(-2m-n)2; (4)(2x+3y)(-2x-3y).
例 3
解题秘方:确定公式中的“a”和“b”,利用完全平方公式进行计算.
感悟新知
知2-练
解:(1)(x+7y)2
=x2+2·x·7y+(7y)2
=x2+14xy+49y2.
(2)(-4a+5b)2
=(5b-4a)2
=(5b)2-2·5b·4a+(4a)2
=25b2-40ab+16a2.
括号不能漏掉.
不能漏掉“2ab”项,且符号
与完全平方中的符号一致.
感悟新知
知2-练
(3)(-2m-n)2
=(2m+n)2
=(2m)2+2·2m·n+n2
=4m2+4mn+n2.
感悟新知
知2-练
(4)(2x+3y)(-2x-3y)
=-(2x+3y)2
=-[(2x)2+2·2x·3y+(3y)2]
=-(4x2+12xy+9y2)=-4x2-12xy-9y2.
两个二项式相乘,若有一项相同,另一项相反,则用平方差公式计算;若两项都相同或都相反,则用完全平方公式计算.
感悟新知
知2-练
3-1.[中考·怀化] 下列计算正确的是( )
A.(x+y)2=x2+y2
B.(x-y)2=x2-2xy-y2
C.(x+1)(x-1)=x2-1
D. (x-1)2=x2-1
C
感悟新知
知2-练
3-2. 计算:
(1)(2y-1)2;
(2)(3a+2b)2;
(3) (-x+2y)2;
(4)(-2xy-1)2.
感悟新知
知2-练
解:(1)原式=(2y)2-2·2y·1+12=4y2-4y+1.
(2)原式=(3a)2+2·3a·2b+(2b)2=9a2+12ab+4b2.
(3)原式=(-x)2+2·(-x)·2y+(2y)2=x2-4xy+4y2.
(4)原式=(2xy+1)2=(2xy)2+2·2xy·1+12=
4x2y2+4xy+1.
感悟新知
知2-练
计算:(1)9992;(2)
例4
解题秘方:将原数转化成符合完全平方公式的形式,再利用完全平方公式展开计算即可.
感悟新知
知2-练
解:(1)9992=(1 000-1)2=1 0002-2×1 000×1+12=
1 000 000-2 000+1=998 001.
感悟新知
知2-练
4-1. 运用完全平方公式进行简便计算:
(1)1022;
(2)99.82;
(3)
感悟新知
知2-练
解:(1)原式=(100+2)2=10 000+400+4=10 404.
(2)原式=(100-0.2)2=10 000-40+0.04=9 960.04.
课堂小结
乘法公式
乘法
公式
平方差公式
两数和(差)
的平方公式
12.3 乘法公式
第12章 整数的乘除
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
两数和乘以这两数的差
两数和(差)的平方公式
知识点
两数和乘以这两数的差
知1-讲
感悟新知
1
1. 平方差公式 两数和与这两数差的积,等于这两数的平方差,这个公式叫做两数和与这两数差的乘法公式,有时也简称为平方差公式.
即:用字母表示为(a+b)(a-b)=a2-b2.
知1-讲
感悟新知
特别解读
公式的特征:
1. 等号左边是两个二项式相乘,这两个二项式中有一项完全相同,另一项互为相反数;
2. 等号右边是乘式中两项的平方差,即相同项的平方减去相反项的平方;
3. 理解字母a、b的意义,平方差公式中的a、b既可代表一个单项式,也可代表一个多项式.
知1-讲
感悟新知
2. 平方差公式的几种常见变化及应用
变化形式 应用举例
位置变化 (b+a)(-b+a)=(a+b)(a-b)=a2-b2
符号变化 (-a-b)(a-b)=(-b-a)(-b+a)=(-b)2-a2=b2-a2
系数变化 (3a+2b)(3a-2b)=(3a)2-(2b)2 =9a2-4b2
指数变化 (a3+b2)(a3-b2)=(a3)2-(b2)2 =a6-b4
增项变化 (a-b+c)(a-b-c)=(a-b)2-c2
连用公式 (a+b)(a-b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4
感悟新知
知1-练
计算:
(1)(5m-3n)(5m+3n);(2)(-2a2+5b)(-2a2-5b);
(3) (4)(-3y-4x)(3y-4x).
例 1
解题秘方:先确定公式中的“a”和“b”,然后根据平方差公式(a+b)(a-b)=a2-b2 进行计算.
感悟新知
知1-练
解法提醒:运用平方差公式计算的三个关键步骤:
第1 步,利用加法的交换律调整两个二项式中项的位置,使之与公式左边相对应,已对应的就不需调整,如(1)(2)不需调整,(3)(4)就必须调整.
第2步,找准公式中的a、b 分别代表哪个单项式或多项式.
第3 步,套用公式计算,注意将底数带上括号. 如(1)中(5m)2不能写成5m2.
感悟新知
知1-练
解:(1)(5m-3n)(5m+3n)=(5m)2-(3n)2=25m2-9n2.
(2)(-2a2+5b)(-2a2-5b)=(-2a2)2-(5b)2=4a4-25b2.
(4)(-3y-4x)(3y-4x)=(-4x-3y)( -4x+3y)=(-4x)2-(3y)2=16x2-9y2.
感悟新知
知1-练
1-1. 若(2-x)(2+x)·(4+x2)=16-xn, 则n的值等于( )
A. 6 B. 4 C. 3 D. 2
1-2. 若(2x+3y)(mx-ny)=9y2-4x2, 则( )
A. m=2, n=3 B. m=-2, n=-3
C. m=2, n=-3 D. m=-2, n=3
B
B
感悟新知
知1-练
1-3. 计算:
(1)(2-3b)(2a+3b);
(2)(-2a-1)(-1+2a);
(4)(1+a)(1-a)+a(a-2).
感悟新知
知1-练
解:(1)原式=(2a)2-(3b)2=4a2-9b2.
(2)原式=(-1-2a)(-1+2a)=(-1)2-(2a)2=1-4a2.
(4)原式=1-a2+a2-2a=1-2a.
感悟新知
知1-练
计算:
(1)10.3×9.7;(2)2 022×2 024-2 0232.
解题秘方:找出平方差公式的模型,利用平方差公式进行计算.
例2
感悟新知
知1-练
解:(1)10.3×9.7
=(10+0.3)×(10-0.3)
=102-0.32
=100-0.09
=99.91.
10.3与9.7的平均数为10.
感悟新知
知1-练
(2)2 022×2 024-2 0232
=(2 023-1)×(2 023+1) -2 0232
=2 0232-1-2 0232
=-1.
2022与2024的平均数为2023.
感悟新知
知1-练
2-1. 运用平方差公式进行简便计算:
(1)9.8×10.2;
(2)1 007×993;
(3)129×127-1282.
感悟新知
知1-练
解:(1)原式=(10-0.2)×(10+0.2)=102-0.22=100-0.04=99.96.
(2)原式=(1 000+7)×(1 000-7)=1 0002-72=1 000 000-49=999 951.
(3)原式=(128+1)×(128-1)-1282=1282-12-1282=-1.
知识点
两数和(差)的平方公式
知2-讲
感悟新知
2
1. 两数和(差)的平方公式(也称完全平方公式) 两数和(差)的平方,等于这两数的平方和加上(减去)它们的积的2 倍.
即: 用字母表示为(a+b)2=a2+2ab+b2,(a-b)2=
a2-2ab+b2.
知2-讲
感悟新知
2. 两数和(差)的平方公式的几种常见变形公式
(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab;
(2)(a+b)2=(a-b)2 +4ab;
(3)(a-b)2=(a+b)2-4ab;
(4)(a+b)2+(a-b)2=2(a2+b2);
(5)(a+b)2 - (a-b)2 =4ab;
知2-讲
感悟新知
(6)ab= [(a+b)2-(a2+b2)]= [(a+b)2-(a-b)2];
(7)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(8)a2+b2+c2+ab+ac+bc= [(a+b)2+(b+c)2+(a+c)2 ]
知2-讲
感悟新知
特别解读
1. 弄清公式的特征:公式的左边是一个二项式的平方,公式的右边是一个三项式,包括左边二项式的各项的平方和,另一项是这两项的乘积的2 倍.
2. 理解字母a、b 的意义:公式中的字母a、b 可以表示具体的数,也可以表示含字母的单项式或多项式.
感悟新知
知2-练
计算:
(1)(x+7y)2; (2)(-4a+5b)2;
(3)(-2m-n)2; (4)(2x+3y)(-2x-3y).
例 3
解题秘方:确定公式中的“a”和“b”,利用完全平方公式进行计算.
感悟新知
知2-练
解:(1)(x+7y)2
=x2+2·x·7y+(7y)2
=x2+14xy+49y2.
(2)(-4a+5b)2
=(5b-4a)2
=(5b)2-2·5b·4a+(4a)2
=25b2-40ab+16a2.
括号不能漏掉.
不能漏掉“2ab”项,且符号
与完全平方中的符号一致.
感悟新知
知2-练
(3)(-2m-n)2
=(2m+n)2
=(2m)2+2·2m·n+n2
=4m2+4mn+n2.
感悟新知
知2-练
(4)(2x+3y)(-2x-3y)
=-(2x+3y)2
=-[(2x)2+2·2x·3y+(3y)2]
=-(4x2+12xy+9y2)=-4x2-12xy-9y2.
两个二项式相乘,若有一项相同,另一项相反,则用平方差公式计算;若两项都相同或都相反,则用完全平方公式计算.
感悟新知
知2-练
3-1.[中考·怀化] 下列计算正确的是( )
A.(x+y)2=x2+y2
B.(x-y)2=x2-2xy-y2
C.(x+1)(x-1)=x2-1
D. (x-1)2=x2-1
C
感悟新知
知2-练
3-2. 计算:
(1)(2y-1)2;
(2)(3a+2b)2;
(3) (-x+2y)2;
(4)(-2xy-1)2.
感悟新知
知2-练
解:(1)原式=(2y)2-2·2y·1+12=4y2-4y+1.
(2)原式=(3a)2+2·3a·2b+(2b)2=9a2+12ab+4b2.
(3)原式=(-x)2+2·(-x)·2y+(2y)2=x2-4xy+4y2.
(4)原式=(2xy+1)2=(2xy)2+2·2xy·1+12=
4x2y2+4xy+1.
感悟新知
知2-练
计算:(1)9992;(2)
例4
解题秘方:将原数转化成符合完全平方公式的形式,再利用完全平方公式展开计算即可.
感悟新知
知2-练
解:(1)9992=(1 000-1)2=1 0002-2×1 000×1+12=
1 000 000-2 000+1=998 001.
感悟新知
知2-练
4-1. 运用完全平方公式进行简便计算:
(1)1022;
(2)99.82;
(3)
感悟新知
知2-练
解:(1)原式=(100+2)2=10 000+400+4=10 404.
(2)原式=(100-0.2)2=10 000-40+0.04=9 960.04.
课堂小结
乘法公式
乘法
公式
平方差公式
两数和(差)
的平方公式
