华师大版 八年级上册 12.4整式的除法 课件(共17张PPT)
文档属性
| 名称 | 华师大版 八年级上册 12.4整式的除法 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 801.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 09:56:03 | ||
图片预览






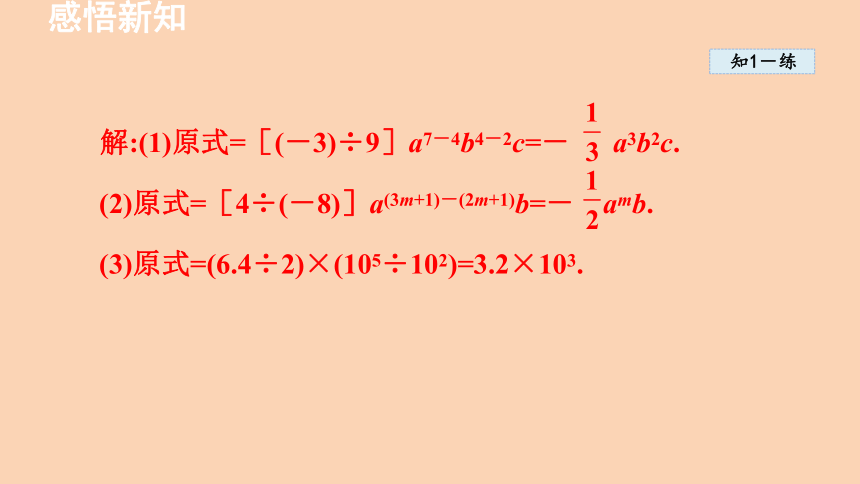
文档简介
(共17张PPT)
12.4 整式的除法
第12章 整数的乘除
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
单项式除以单项式
多项式除以单项式
知识点
单项式除以单项式
知1-讲
感悟新知
1
1. 单项式除以单项式法则 单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
知1-讲
感悟新知
2. 步骤:
(1)把系数相除,所得结果作为商的系数.
(2)把同底数幂分别相除,所得的结果作为商的因式.
(3)把只在被除式里出现的字母,连同它的指数一起作为商的一个因式.
知1-讲
感悟新知
特别解读
1. 单项式除以单项式最终转化为同底数幂相除.
2. 单项式除以单项式的结果还是单项式.
3. 根据乘除互逆的原则,可用单项式乘法来验证结果.
感悟新知
知1-练
计算:
(1)-3a7b4c÷9a4b2; (2)4a3m+1b÷(-8a2m+1);
(3)(6.4×105)÷(2×102).
例 1
解题秘方:根据单项式除以单项式法则计算.
感悟新知
知1-练
解:(1)原式=[(-3)÷9]a7-4b4-2c=- a3b2c.
(2)原式=[4÷(-8)]a(3m+1)-(2m+1)b=- amb.
(3)原式=(6.4÷2)×(105÷102)=3.2×103.
感悟新知
知1-练
1-1. 计算:
感悟新知
知1-练
知识点
多项式除以单项式
知2-讲
感悟新知
2
1. 多项式除以单项式法则 多项式除以单项式,先用这个多项式的每一项除以这个单项式,再把所得的商相加.
即:用字母表示为(am+bm)÷m=am÷m+bm÷m=a+b.
2. 步骤
(1)用多项式的每一项除以单项式;
(2)把每一项除得的商相加.
知2-讲
感悟新知
特别解读
1. 多项式除以单项式的实质就是转化为单项式除以单项式.
2. 商的项数与多项式的项数相同.
3. 用多项式的每一项除以单项式时,包括每一项的符号.
感悟新知
知2-练
计算:
(1)(8a3-2a2+6a)÷(-2a);
例2
解题秘方:先把多项式的每一项除以单项式,再把所得的商相加.
感悟新知
知2-练
解:(1)(8a3-2a2+6a)÷(-2a)=8a3÷(-2a)+
(-2a2)÷-2a)+6a÷(-2a)=-4a2+a-3.
感悟新知
知2-练
B
2-1. 如果(4a2b-3ab2)÷M=-4a+3b,那么单项式M 为( )
A.ab B. -ab C.a D. -b
感悟新知
知2-练
2-2. 计算:
(1)(12a3-6a2)÷(-2a);
(2)(4x3y-6x2y2)÷2xy;
(3) (x5y3- 2x4y3 +3x2y) ÷x2y;
(4)
感悟新知
知2-练
解:(1)原式=12a3÷(-2a)+(-6a2)÷(-2a)=-6a2+3a.
(2)原式=4x3y÷2xy+(-6x2y2)÷2xy=2x2-3xy.
(3)原式=x5y3÷x2y+(-2x4y3)÷x2y+3x2y÷x2y=x3y2-2x2y2+3.
课堂小结
整式的除法
整式的除法
关键
同底数幂的除法
单项式除以单项式
多项式除以单项式
转 化
12.4 整式的除法
第12章 整数的乘除
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
单项式除以单项式
多项式除以单项式
知识点
单项式除以单项式
知1-讲
感悟新知
1
1. 单项式除以单项式法则 单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
知1-讲
感悟新知
2. 步骤:
(1)把系数相除,所得结果作为商的系数.
(2)把同底数幂分别相除,所得的结果作为商的因式.
(3)把只在被除式里出现的字母,连同它的指数一起作为商的一个因式.
知1-讲
感悟新知
特别解读
1. 单项式除以单项式最终转化为同底数幂相除.
2. 单项式除以单项式的结果还是单项式.
3. 根据乘除互逆的原则,可用单项式乘法来验证结果.
感悟新知
知1-练
计算:
(1)-3a7b4c÷9a4b2; (2)4a3m+1b÷(-8a2m+1);
(3)(6.4×105)÷(2×102).
例 1
解题秘方:根据单项式除以单项式法则计算.
感悟新知
知1-练
解:(1)原式=[(-3)÷9]a7-4b4-2c=- a3b2c.
(2)原式=[4÷(-8)]a(3m+1)-(2m+1)b=- amb.
(3)原式=(6.4÷2)×(105÷102)=3.2×103.
感悟新知
知1-练
1-1. 计算:
感悟新知
知1-练
知识点
多项式除以单项式
知2-讲
感悟新知
2
1. 多项式除以单项式法则 多项式除以单项式,先用这个多项式的每一项除以这个单项式,再把所得的商相加.
即:用字母表示为(am+bm)÷m=am÷m+bm÷m=a+b.
2. 步骤
(1)用多项式的每一项除以单项式;
(2)把每一项除得的商相加.
知2-讲
感悟新知
特别解读
1. 多项式除以单项式的实质就是转化为单项式除以单项式.
2. 商的项数与多项式的项数相同.
3. 用多项式的每一项除以单项式时,包括每一项的符号.
感悟新知
知2-练
计算:
(1)(8a3-2a2+6a)÷(-2a);
例2
解题秘方:先把多项式的每一项除以单项式,再把所得的商相加.
感悟新知
知2-练
解:(1)(8a3-2a2+6a)÷(-2a)=8a3÷(-2a)+
(-2a2)÷-2a)+6a÷(-2a)=-4a2+a-3.
感悟新知
知2-练
B
2-1. 如果(4a2b-3ab2)÷M=-4a+3b,那么单项式M 为( )
A.ab B. -ab C.a D. -b
感悟新知
知2-练
2-2. 计算:
(1)(12a3-6a2)÷(-2a);
(2)(4x3y-6x2y2)÷2xy;
(3) (x5y3- 2x4y3 +3x2y) ÷x2y;
(4)
感悟新知
知2-练
解:(1)原式=12a3÷(-2a)+(-6a2)÷(-2a)=-6a2+3a.
(2)原式=4x3y÷2xy+(-6x2y2)÷2xy=2x2-3xy.
(3)原式=x5y3÷x2y+(-2x4y3)÷x2y+3x2y÷x2y=x3y2-2x2y2+3.
课堂小结
整式的除法
整式的除法
关键
同底数幂的除法
单项式除以单项式
多项式除以单项式
转 化
