13.2.2三角形全等的判定 课件
图片预览






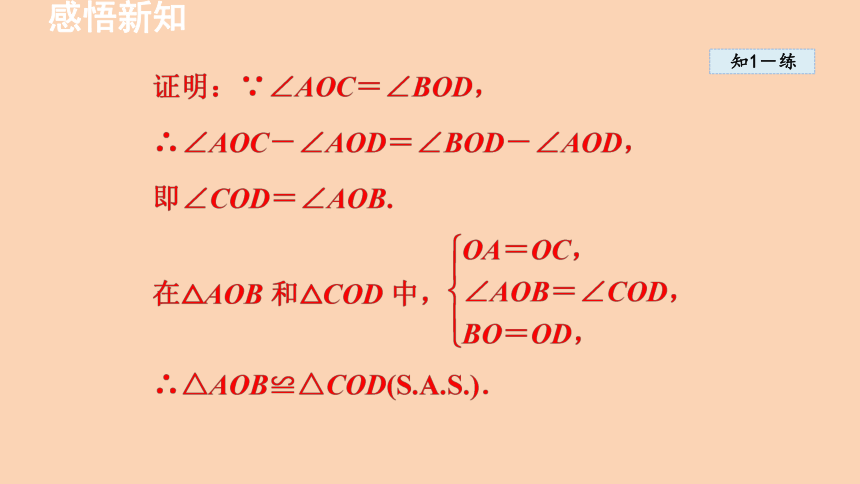

文档简介
(共44张PPT)
13.2 三角形全等的判定
第13章 全等三角形
13.2.2 三角形全等的判定
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
边角边
角边角
角角边
边边边
斜边直角边
知识点
边角边
知1-讲
感悟新知
1
1. 基本事实 两边及其夹角分别相等的两个三角形全等. 简记为S.A.S.(或边角边).
知1-讲
感悟新知
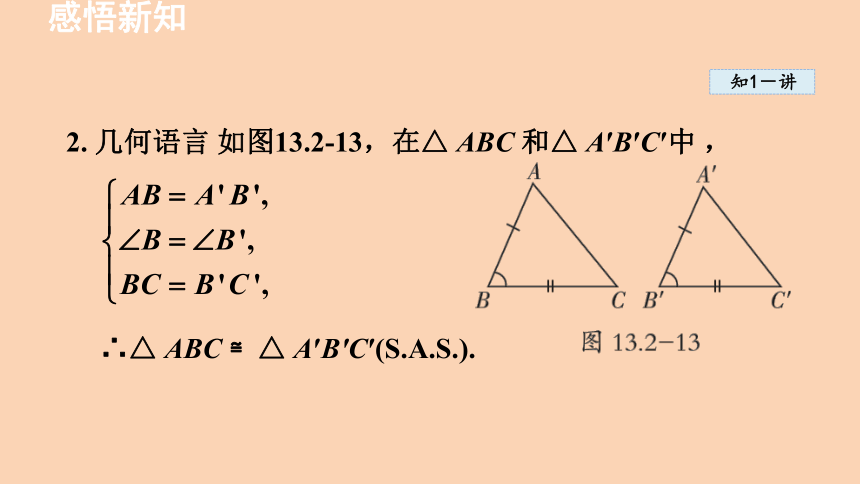
2. 几何语言 如图13.2-13,在△ ABC 和△ A′B′C′中 ,
∴△ ABC ≌△ A′B′C′(S.A.S.).
知1-讲
感悟新知
特别提醒
在列举两个三角形全等的条件时,应把三个条件按顺序排列(一般是把同一个三角形的三个条件放在等号的同一侧)并用大括号将其括起来.
感悟新知
知1-练
如图13.2-14, 点C 是AB 的中点,AD=CE, 且
AD ∥ CE. 求证:△ ACD ≌△ CBE.
例 1
解题秘方:根据条件找出两个三角形中的两条边及其夹角对应相等,根据“S.A.S.”判定两个三角形全等.
感悟新知
知1-练
方法提醒:证明两个三角形全等,既要注意全等的书写形式,又要注意未知元素在证明全等时必须先做好推理.
感悟新知
知1-练
证明:∵点C 是AB 的中点,∴ AC=CB.
∵ AD ∥ CE,∴∠ CAD= ∠ BCE.
在△ ACD 和△ CBE 中,
∴△ ACD ≌△ CBE(S.A.S.).
感悟新知
知1-练
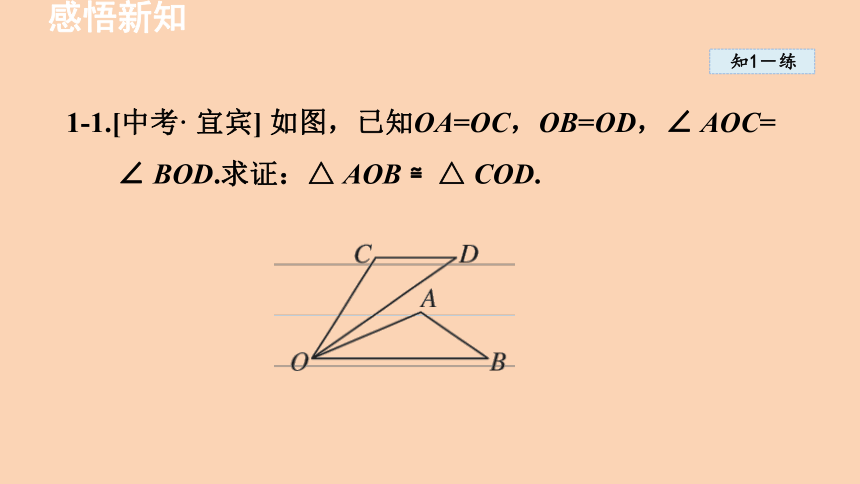
1-1.[中考· 宜宾] 如图,已知OA=OC,OB=OD,∠ AOC= ∠ BOD.求证:△ AOB ≌△ COD.
感悟新知
知1-练
知识点
角边角
知2-讲
感悟新知
2
1. 基本事实 两角及其夹边分别相等的两个三角形全等. 简记为A.S.A.(或角边角).
知2-讲
感悟新知
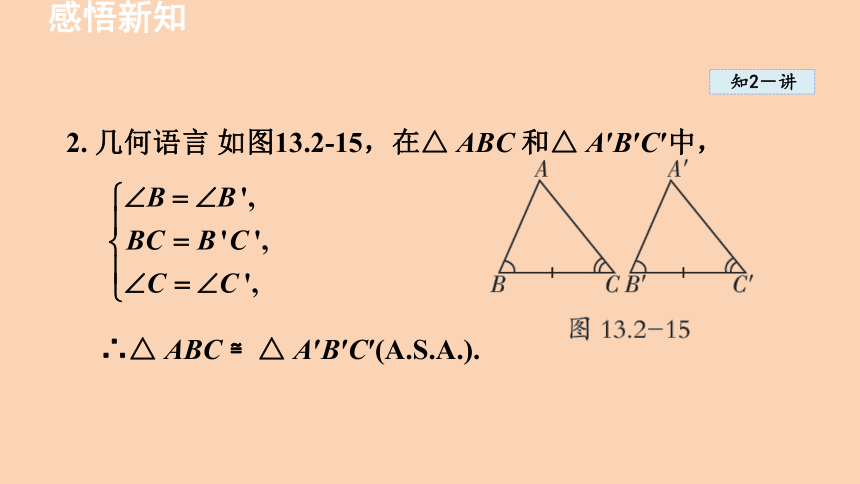
2. 几何语言 如图13.2-15,在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△ A′B′C′(A.S.A.).
知2-讲
感悟新知
特别解读
1. 相等的元素:两角及两角的夹边.
2. 书写顺序:角→边→角.
3. 夹边即两个角的公共边.
感悟新知
知2-练
如图13.2-16,已知AB ∥ DF,AC ∥ DE,BC=FE,
且点B、E、C、F 在同一条直线上. 求证:△ ABC ≌△ DFE.
例2
解题秘方:解题的关键是由两组平行线得出两组角对应相等,构造两角及其夹边对应相等.
感悟新知
知2-练
证明:∵ AB ∥ DF,且点B、E、C、F 在同一条直线上,∴∠ B= ∠ F.
∵ AC ∥ DE,∴∠ ACB= ∠ DEF.
在△ ABC 和△ DFE 中,
∴△ ABC ≌△ DFE(A.S.A.).
感悟新知
知2-练
2-1. 如图,某同学把一块三角形的玻璃打碎成了3 块,现在要去玻璃店配一块完全一样的玻璃,其中最省事的办法是( )
A. 带①去
B. 带②去
C. 带③去
D. 带①和②去
C
知识点
角角边
知3-讲
感悟新知
3
1. 定理 两角分别相等且其中一组等角的对边相等的两个三角形全等. 简记为A.A.S.(或角角边).
知3-讲
感悟新知
2. 几何语言 如图13.2-17,在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△A′B′C′(A.A.S.).
知3-讲
感悟新知
3.“A.S.A.”与“A.A.S.”的区别与联系
“S”的意义 书写格式 联系
A.S.A. “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形内角和定理可知,“A.A.S.”可由“A.S.A.”推导得出
A.A.S. “S”是其中一角的对边 把两角相等写在一起,边相等放在最后
知3-讲
感悟新知
特别解读
1. 判定两个三角形全等的三个条件中,“边”是必不可少的.
2. 由于“角角边”和“角边角”是可以互相转化的,故能用“角角边”证明的问题,一般也可以用“角边角”证明.
感悟新知
知3-练
如图13.2-18, 已知AB=AC,AD=AE. 求证:
△ BOD ≌△ COE.
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“A.A.S.”判定两个三角形全等.
例 3
感悟新知
知3-练
证明:在△ ABE 和△ ACD 中,
∴△ ABE ≌△ ACD(S.A.S.).
∴∠ B= ∠ C.
∵ AB=AC,AD=AE,∴ BD=CE.
在△ BOD 和△ COE 中,
∴△ BOD ≌△ COE(A.A.S.).
感悟新知
知3-练
3-1.[中考·玉林] 如图,AB=AE, ∠ 1= ∠ 2,∠ C= ∠ D. 求证:△ ABC ≌△ AED.
感悟新知
知3-练
知识点
边边边
知4-讲
感悟新知
4
1. 基本事实 三边分别相等的两个三角形全等. 简记为S.S.S.(或边边边).
知4-讲
感悟新知
2. 几何语言 如图13.2-19,
在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△ A′B′C′(S.S.S.).
知4-讲
感悟新知
特别解读
在两个三角形的六个元素(三条边和三个角)中,由已知的三个元素可判定两个三角形全等的组合有4 个:“S.S.S.”“S.A.S.”“A.S.A.”和“A.A.S.”,不能判定两个三角形全等的组合是“A.A.A.”和“S.S.A.”.
感悟新知
知4-练
如图13.2-20,已知点A、D、B、F 在同一条直线上,AC= FE,BC = DE,AD = FB. 求证:△ ABC ≌△ FDE.
解题秘方:紧扣“S.S.S.”找出两个三角形中三边对应相等的条件来判定两个三角形全等.
例4
感悟新知
知4-练
证明:∵ AD=FB,
∴ AD+DB=FB+DB,
即AB=FD.
在△ ABC 和△ FDE 中,
∴△ ABC ≌△ FDE(S.S.S.).
感悟新知
知4-练
4-1. 如图, 在四边形ABCD 中,AB=CD,AD=CB,连结AC. 求证:△ ABC ≌△ CDA.
感悟新知
知4-练
知识点
斜边直角边
知5-讲
感悟新知
5
1. 定理 斜边和一条直角边分别相等的两个直角三角形全等. 简记为H.L.(或斜边直角边).
知5-讲
感悟新知
2. 几何语言 如图13.2-21, 在
Rt △ ABC 和Rt △ A′B′C′中 ,
∴ Rt △ ABC ≌ Rt △ A′B′C′(H.L.).
知5-讲
感悟新知
3. 判定两个三角形全等常用的思路方法如下表
知5-讲
感悟新知
已知对应
相等的元素 可选择的
判定方法 需寻找的条件
锐角三角形或钝角三角形 两边(SS) S.S.S. 或S.A.S. 可证第三边对应相等或证两边的夹角对应相等
一边及其邻角(SA) S.A.S. 或A.S.A.
或A.A.S. 可证已知角的另一边对应相等或证已知边的另一邻角对应相等或证已知边的对角对应相等
一边及其对角(SA) A.A.S. 可证另一角对应相等
两角(AA) A.S.A. 或A.A.S. 可证两角的夹边对应相等或证相等一角的对边对应相等
知5-讲
感悟新知
直角三角形 一锐角(A) A.S.A. 或A.A.S. 可证直角与已知锐角的夹边对应相等或锐角(或直角)的对边对应相等
斜边(H) H.L. 或A.A.S. 可证一条直角边对应相等或证一锐角对应相等
一直角边(L) H.L. 或S.A.S. 或A.S.A. 或A.A.S. 可证斜边对应相等或证另一直角边对应相等或证与已知边相邻的锐角对应相等或证已知边所对的锐角对应相等
知5-讲
感悟新知
特别提醒
1. 应用“H.L.”判定两个直角三角形全等,在书写时两个三角形符号前一定要加上“Rt”.
2. 判定两个直角三角形全等的特殊方法(“H.L.”),只适用于直角三角形全等的判定,对于一般三角形不适用.
知5-讲
感悟新知
3. 判定一般三角形全等的所有方法对判定两个直角三角形全等同样适用.
4. 在用一般方法证明直角三角形全等时,因为两个直角三角形中已具备一对直角相等的条件,故只需找另外两个条件即可.
感悟新知
知5-练
如图13.2-22,AC ⊥ BC,AD ⊥ BD,AD=BC,
CE ⊥ AB,DF ⊥ AB,垂足分别是点E、F. 求证:CE=DF.
解题秘方:利用“H.L.”证明两个直角三角形全等,为证明两条线段相等创造条件.
例 5
感悟新知
知5-练
证明:∵ AC ⊥ BC,AD ⊥ BD,
∴∠ ACB= ∠ BDA=90°.
在Rt △ ABC 和Rt △ BAD 中,
∴ Rt △ ABC ≌ Rt △ BAD(H.L.). ∴∠ CBE= ∠ DAF.
∵ CE ⊥ AB,DF ⊥ AB,∴∠ CEB=90°,∠ DFA=90°.
感悟新知
知5-练
在△ BCE 和△ ADF 中,
∴△ BCE ≌△ ADF(A.A.S.). ∴ CE=DF.
感悟新知
知5-练
5-1. 如图,小明和小芳以相同的速度分别同时从A、B出发,小明沿AC行走,小芳沿BD 行走,并同时到达C、D. 若CB ⊥ AB,DA ⊥ AB, 则CB 与DA相等吗?为什么?
感悟新知
知5-练
课堂小结
三角形全等的判定
三角形全等的判定方法
两边及夹角(S.A.S.)
两角一边
(A.S.A. 或A.A.S.)
三边(S.S.S.)
斜边直角边(H.L.)
直角三
角形全
等的判
定方法
13.2 三角形全等的判定
第13章 全等三角形
13.2.2 三角形全等的判定
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
边角边
角边角
角角边
边边边
斜边直角边
知识点
边角边
知1-讲
感悟新知
1
1. 基本事实 两边及其夹角分别相等的两个三角形全等. 简记为S.A.S.(或边角边).
知1-讲
感悟新知
2. 几何语言 如图13.2-13,在△ ABC 和△ A′B′C′中 ,
∴△ ABC ≌△ A′B′C′(S.A.S.).
知1-讲
感悟新知
特别提醒
在列举两个三角形全等的条件时,应把三个条件按顺序排列(一般是把同一个三角形的三个条件放在等号的同一侧)并用大括号将其括起来.
感悟新知
知1-练
如图13.2-14, 点C 是AB 的中点,AD=CE, 且
AD ∥ CE. 求证:△ ACD ≌△ CBE.
例 1
解题秘方:根据条件找出两个三角形中的两条边及其夹角对应相等,根据“S.A.S.”判定两个三角形全等.
感悟新知
知1-练
方法提醒:证明两个三角形全等,既要注意全等的书写形式,又要注意未知元素在证明全等时必须先做好推理.
感悟新知
知1-练
证明:∵点C 是AB 的中点,∴ AC=CB.
∵ AD ∥ CE,∴∠ CAD= ∠ BCE.
在△ ACD 和△ CBE 中,
∴△ ACD ≌△ CBE(S.A.S.).
感悟新知
知1-练
1-1.[中考· 宜宾] 如图,已知OA=OC,OB=OD,∠ AOC= ∠ BOD.求证:△ AOB ≌△ COD.
感悟新知
知1-练
知识点
角边角
知2-讲
感悟新知
2
1. 基本事实 两角及其夹边分别相等的两个三角形全等. 简记为A.S.A.(或角边角).
知2-讲
感悟新知
2. 几何语言 如图13.2-15,在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△ A′B′C′(A.S.A.).
知2-讲
感悟新知
特别解读
1. 相等的元素:两角及两角的夹边.
2. 书写顺序:角→边→角.
3. 夹边即两个角的公共边.
感悟新知
知2-练
如图13.2-16,已知AB ∥ DF,AC ∥ DE,BC=FE,
且点B、E、C、F 在同一条直线上. 求证:△ ABC ≌△ DFE.
例2
解题秘方:解题的关键是由两组平行线得出两组角对应相等,构造两角及其夹边对应相等.
感悟新知
知2-练
证明:∵ AB ∥ DF,且点B、E、C、F 在同一条直线上,∴∠ B= ∠ F.
∵ AC ∥ DE,∴∠ ACB= ∠ DEF.
在△ ABC 和△ DFE 中,
∴△ ABC ≌△ DFE(A.S.A.).
感悟新知
知2-练
2-1. 如图,某同学把一块三角形的玻璃打碎成了3 块,现在要去玻璃店配一块完全一样的玻璃,其中最省事的办法是( )
A. 带①去
B. 带②去
C. 带③去
D. 带①和②去
C
知识点
角角边
知3-讲
感悟新知
3
1. 定理 两角分别相等且其中一组等角的对边相等的两个三角形全等. 简记为A.A.S.(或角角边).
知3-讲
感悟新知
2. 几何语言 如图13.2-17,在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△A′B′C′(A.A.S.).
知3-讲
感悟新知
3.“A.S.A.”与“A.A.S.”的区别与联系
“S”的意义 书写格式 联系
A.S.A. “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形内角和定理可知,“A.A.S.”可由“A.S.A.”推导得出
A.A.S. “S”是其中一角的对边 把两角相等写在一起,边相等放在最后
知3-讲
感悟新知
特别解读
1. 判定两个三角形全等的三个条件中,“边”是必不可少的.
2. 由于“角角边”和“角边角”是可以互相转化的,故能用“角角边”证明的问题,一般也可以用“角边角”证明.
感悟新知
知3-练
如图13.2-18, 已知AB=AC,AD=AE. 求证:
△ BOD ≌△ COE.
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“A.A.S.”判定两个三角形全等.
例 3
感悟新知
知3-练
证明:在△ ABE 和△ ACD 中,
∴△ ABE ≌△ ACD(S.A.S.).
∴∠ B= ∠ C.
∵ AB=AC,AD=AE,∴ BD=CE.
在△ BOD 和△ COE 中,
∴△ BOD ≌△ COE(A.A.S.).
感悟新知
知3-练
3-1.[中考·玉林] 如图,AB=AE, ∠ 1= ∠ 2,∠ C= ∠ D. 求证:△ ABC ≌△ AED.
感悟新知
知3-练
知识点
边边边
知4-讲
感悟新知
4
1. 基本事实 三边分别相等的两个三角形全等. 简记为S.S.S.(或边边边).
知4-讲
感悟新知
2. 几何语言 如图13.2-19,
在△ ABC 和△ A′B′C′中,
∴△ ABC ≌△ A′B′C′(S.S.S.).
知4-讲
感悟新知
特别解读
在两个三角形的六个元素(三条边和三个角)中,由已知的三个元素可判定两个三角形全等的组合有4 个:“S.S.S.”“S.A.S.”“A.S.A.”和“A.A.S.”,不能判定两个三角形全等的组合是“A.A.A.”和“S.S.A.”.
感悟新知
知4-练
如图13.2-20,已知点A、D、B、F 在同一条直线上,AC= FE,BC = DE,AD = FB. 求证:△ ABC ≌△ FDE.
解题秘方:紧扣“S.S.S.”找出两个三角形中三边对应相等的条件来判定两个三角形全等.
例4
感悟新知
知4-练
证明:∵ AD=FB,
∴ AD+DB=FB+DB,
即AB=FD.
在△ ABC 和△ FDE 中,
∴△ ABC ≌△ FDE(S.S.S.).
感悟新知
知4-练
4-1. 如图, 在四边形ABCD 中,AB=CD,AD=CB,连结AC. 求证:△ ABC ≌△ CDA.
感悟新知
知4-练
知识点
斜边直角边
知5-讲
感悟新知
5
1. 定理 斜边和一条直角边分别相等的两个直角三角形全等. 简记为H.L.(或斜边直角边).
知5-讲
感悟新知
2. 几何语言 如图13.2-21, 在
Rt △ ABC 和Rt △ A′B′C′中 ,
∴ Rt △ ABC ≌ Rt △ A′B′C′(H.L.).
知5-讲
感悟新知
3. 判定两个三角形全等常用的思路方法如下表
知5-讲
感悟新知
已知对应
相等的元素 可选择的
判定方法 需寻找的条件
锐角三角形或钝角三角形 两边(SS) S.S.S. 或S.A.S. 可证第三边对应相等或证两边的夹角对应相等
一边及其邻角(SA) S.A.S. 或A.S.A.
或A.A.S. 可证已知角的另一边对应相等或证已知边的另一邻角对应相等或证已知边的对角对应相等
一边及其对角(SA) A.A.S. 可证另一角对应相等
两角(AA) A.S.A. 或A.A.S. 可证两角的夹边对应相等或证相等一角的对边对应相等
知5-讲
感悟新知
直角三角形 一锐角(A) A.S.A. 或A.A.S. 可证直角与已知锐角的夹边对应相等或锐角(或直角)的对边对应相等
斜边(H) H.L. 或A.A.S. 可证一条直角边对应相等或证一锐角对应相等
一直角边(L) H.L. 或S.A.S. 或A.S.A. 或A.A.S. 可证斜边对应相等或证另一直角边对应相等或证与已知边相邻的锐角对应相等或证已知边所对的锐角对应相等
知5-讲
感悟新知
特别提醒
1. 应用“H.L.”判定两个直角三角形全等,在书写时两个三角形符号前一定要加上“Rt”.
2. 判定两个直角三角形全等的特殊方法(“H.L.”),只适用于直角三角形全等的判定,对于一般三角形不适用.
知5-讲
感悟新知
3. 判定一般三角形全等的所有方法对判定两个直角三角形全等同样适用.
4. 在用一般方法证明直角三角形全等时,因为两个直角三角形中已具备一对直角相等的条件,故只需找另外两个条件即可.
感悟新知
知5-练
如图13.2-22,AC ⊥ BC,AD ⊥ BD,AD=BC,
CE ⊥ AB,DF ⊥ AB,垂足分别是点E、F. 求证:CE=DF.
解题秘方:利用“H.L.”证明两个直角三角形全等,为证明两条线段相等创造条件.
例 5
感悟新知
知5-练
证明:∵ AC ⊥ BC,AD ⊥ BD,
∴∠ ACB= ∠ BDA=90°.
在Rt △ ABC 和Rt △ BAD 中,
∴ Rt △ ABC ≌ Rt △ BAD(H.L.). ∴∠ CBE= ∠ DAF.
∵ CE ⊥ AB,DF ⊥ AB,∴∠ CEB=90°,∠ DFA=90°.
感悟新知
知5-练
在△ BCE 和△ ADF 中,
∴△ BCE ≌△ ADF(A.A.S.). ∴ CE=DF.
感悟新知
知5-练
5-1. 如图,小明和小芳以相同的速度分别同时从A、B出发,小明沿AC行走,小芳沿BD 行走,并同时到达C、D. 若CB ⊥ AB,DA ⊥ AB, 则CB 与DA相等吗?为什么?
感悟新知
知5-练
课堂小结
三角形全等的判定
三角形全等的判定方法
两边及夹角(S.A.S.)
两角一边
(A.S.A. 或A.A.S.)
三边(S.S.S.)
斜边直角边(H.L.)
直角三
角形全
等的判
定方法
