第十八章 平行四边形单元同步检测试题(含答案)
文档属性
| 名称 | 第十八章 平行四边形单元同步检测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 556.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-28 17:38:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为( )
A.20 B.30 C.40 D.50
2. 已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
3. 对于任意的矩形,下列说法一定正确的是
A.对角线垂直且相等 B.四边都互相垂直
C.四个角都相等 D.是轴对称图形,但不是中心对称图形
4. 如图2所示,已知等边三角形ABC的边长为,按图中所示的规律,用个这样的三角形镶嵌而成的四边形的周长是( )
A. B. C. D.
5.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.7 B.8 C.9 D.10
6.如图,四边形ABCD为菱形,点A的坐标为(4,0),点C的坐标为(4,4),点D在y轴上,则点B的坐标为( )
A.(4,2) B.(2,8) C.(8,4) D.(8,2)
7.如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
8.如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6米 B.6米 C.3米 D.3米
9.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形 B.矩形的对角线互相垂直
C.一组对边平行的四边形是平行四边形 D.四边相等的四边形是菱形
10.如图,E,F分别是 ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
A.6 B.12 C.18 D.24
二、填空题(每题3分,共30分)
11.在 ABCD中,如果∠A+∠C=140°,那么∠B=________度.
12.把两根长度相等的木条的中点用螺栓固定在一起,依次连接木条的四个端点得到的四边形是________.
13.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME= .
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为 .
如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,连接PB,PD.若PB=2,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为________.
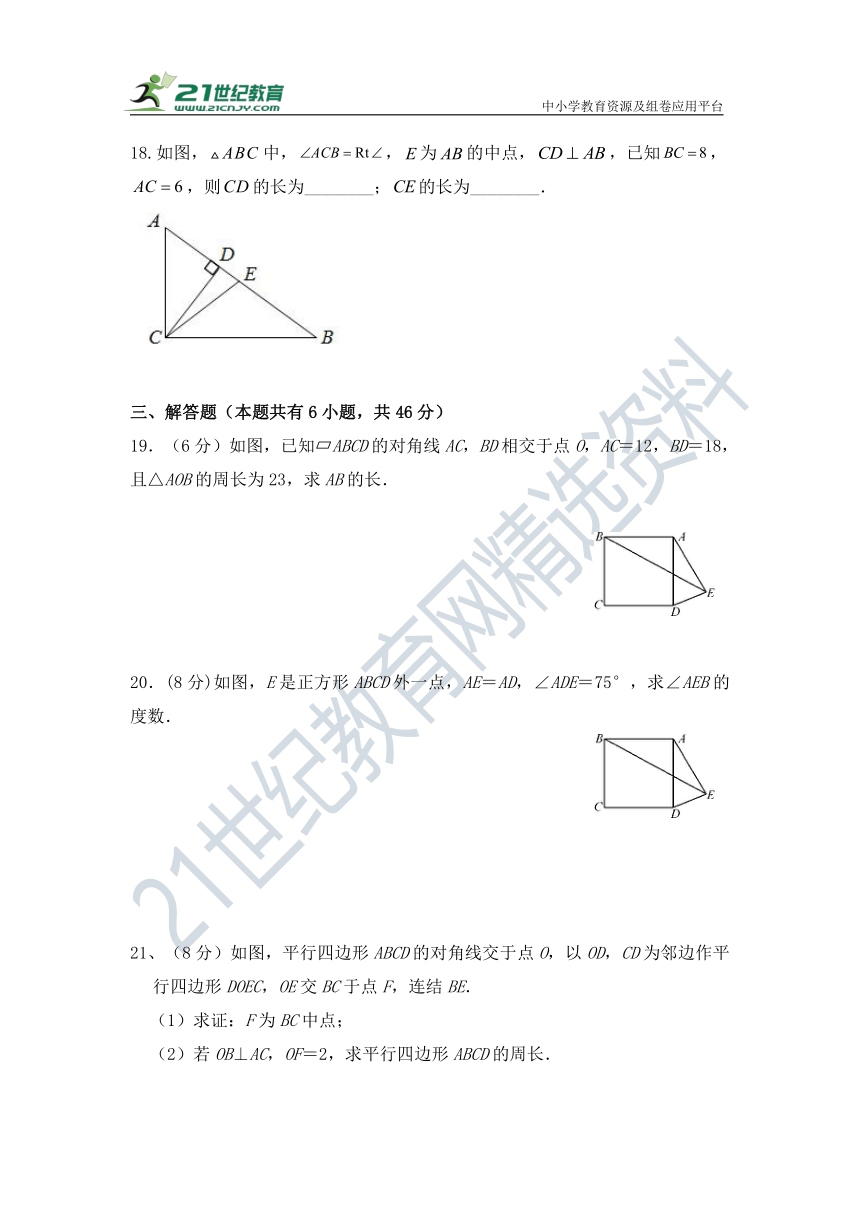
18.如图,中,,为的中点,,已知,,则的长为________;的长为________.
三、解答题(本题共有6小题,共46分)
19.(6分)如图,已知 ABCD的对角线AC,BD相交于点O,AC=12,BD=18,且△AOB的周长为23,求AB的长.
20.(8分)如图,E是正方形ABCD外一点,AE=AD,∠ADE=75°,求∠AEB的度数.
21、(8分)如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.
(1)求证:F为BC中点;
(2)若OB⊥AC,OF=2,求平行四边形ABCD的周长.
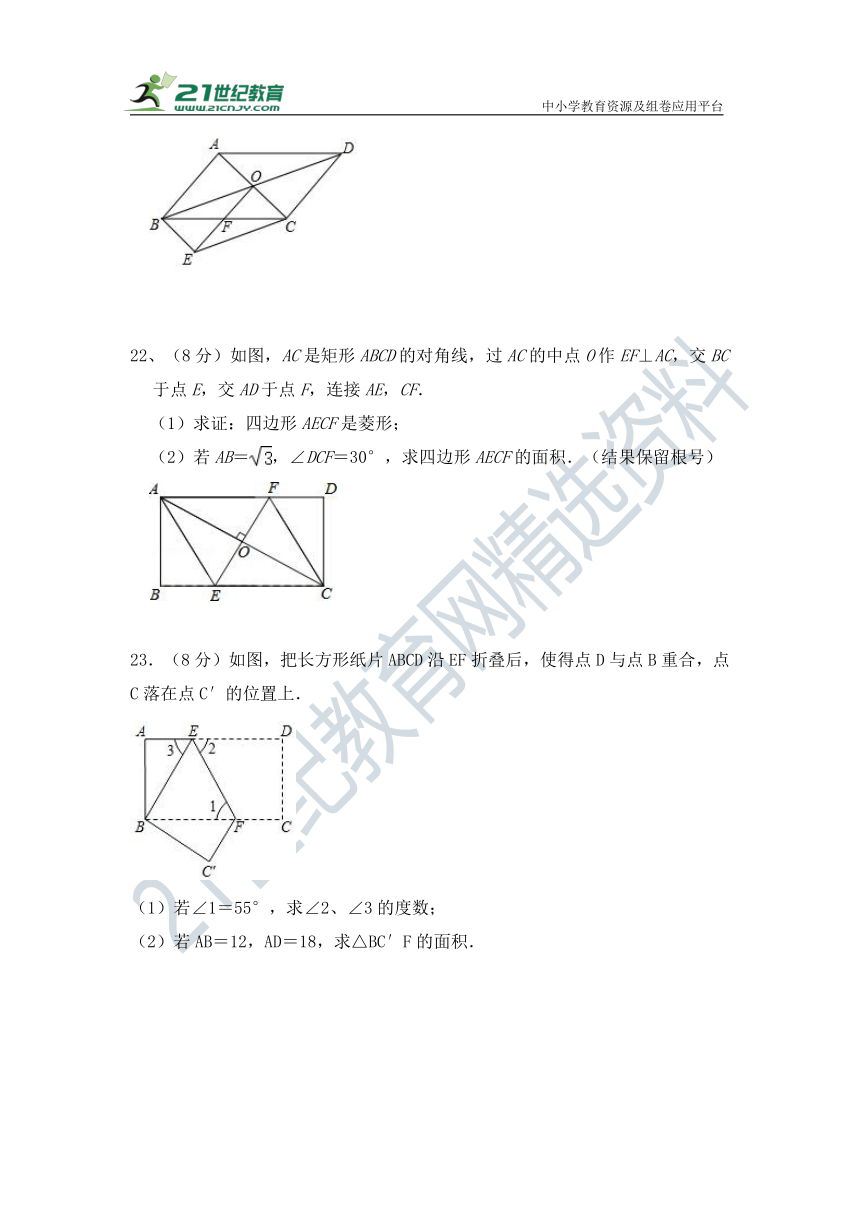
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.(8分)如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=55°,求∠2、∠3的度数;
(2)若AB=12,AD=18,求△BC′F的面积.
24.(8分)如图,中,,,,点D为的中点,动点P从点A出发,沿方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,也以每秒1个单位的速度沿方向运动到点B,以,为邻边构造,设点P运动的时间为t秒.
(1)当时,求的长;
(2)如图2,当点Q运动至点B时,连结,求证:.
(3)如图3,连结,当点E恰好落在的边上时,求所有满足要求的t值.
参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C C B D A A D C
二.填空题
11.110
12.矩形
13.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是8.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为12.
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°.
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为150°.
.2+6
18.4.8 5
三、解答题
19.∵四边形ABCD是平行四边形,∴OA=AC=6,OB=BD=9.∵OA+OB+AB=23,∴AB=23-6-9=8.
20.∵在△ADE中,AE=AD,∠ADE=75°,∴∠AED=75°(等边对等角),∴∠EAD=180°-75°×2=30°,又∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴△ABE中,AB=AE,∠BAE=120°∴∠AEB=(180°-120°)=30°.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23.(1)∠2=55°,∠3=70°;(2)
24.(1)解:由题意可得:,
∵,,,
∴,
∵点D为的中点,
∴,
过点P作PH⊥AB于点H,如图所示:
∵,
∴,
∴,
在Rt△AHP中,,
∴,
∴在Rt△PHD中,;
(2)证明:∵点Q运动至点B时,四边形是平行四边形,
∴PE∥BD,PE=BD,
∵点D为的中点,
∴,
∴PE∥AD,PE=AD,
∴四边形是平行四边形,
∴;
(3)由题意得:,
∵,,,
∴,
当点E恰好落在的边上时,则可分:
①当点E恰好落在的边上时,如图,
∵四边形是平行四边形,
∴PE=DQ,PD=QE,DQ∥AC,
∵∠ACB=90°,
∴,
∵点D为的中点,
∴,
∴,
∴,
∴,即;
②当点E恰好落在的边上时,如图,过点D、E分别作DN⊥BC,EM⊥AC,垂足分别为N、M,
∴,
∵四边形PEQD是平行四边形,
∴,
∴,
∵点D为的中点,
∴,
∴CN=BN,
∴,
由(1)得:,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴在Rt△CME中,,
∵,
∴,
解得:;
由题意可知点E恰好落在的边上是不存在的,
综上所述:当点E恰好落在的边上时,t的值为或.
D
A
C
B
F
E
题
C
A
B
┅┅
《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为( )
A.20 B.30 C.40 D.50
2. 已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
3. 对于任意的矩形,下列说法一定正确的是
A.对角线垂直且相等 B.四边都互相垂直
C.四个角都相等 D.是轴对称图形,但不是中心对称图形
4. 如图2所示,已知等边三角形ABC的边长为,按图中所示的规律,用个这样的三角形镶嵌而成的四边形的周长是( )
A. B. C. D.
5.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.7 B.8 C.9 D.10
6.如图,四边形ABCD为菱形,点A的坐标为(4,0),点C的坐标为(4,4),点D在y轴上,则点B的坐标为( )
A.(4,2) B.(2,8) C.(8,4) D.(8,2)
7.如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
8.如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6米 B.6米 C.3米 D.3米
9.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形 B.矩形的对角线互相垂直
C.一组对边平行的四边形是平行四边形 D.四边相等的四边形是菱形
10.如图,E,F分别是 ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
A.6 B.12 C.18 D.24
二、填空题(每题3分,共30分)
11.在 ABCD中,如果∠A+∠C=140°,那么∠B=________度.
12.把两根长度相等的木条的中点用螺栓固定在一起,依次连接木条的四个端点得到的四边形是________.
13.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME= .
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为 .
如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,连接PB,PD.若PB=2,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为________.
18.如图,中,,为的中点,,已知,,则的长为________;的长为________.
三、解答题(本题共有6小题,共46分)
19.(6分)如图,已知 ABCD的对角线AC,BD相交于点O,AC=12,BD=18,且△AOB的周长为23,求AB的长.
20.(8分)如图,E是正方形ABCD外一点,AE=AD,∠ADE=75°,求∠AEB的度数.
21、(8分)如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.
(1)求证:F为BC中点;
(2)若OB⊥AC,OF=2,求平行四边形ABCD的周长.
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.(8分)如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=55°,求∠2、∠3的度数;
(2)若AB=12,AD=18,求△BC′F的面积.
24.(8分)如图,中,,,,点D为的中点,动点P从点A出发,沿方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,也以每秒1个单位的速度沿方向运动到点B,以,为邻边构造,设点P运动的时间为t秒.
(1)当时,求的长;
(2)如图2,当点Q运动至点B时,连结,求证:.
(3)如图3,连结,当点E恰好落在的边上时,求所有满足要求的t值.
参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C C B D A A D C
二.填空题
11.110
12.矩形
13.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是8.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为12.
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°.
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为150°.
.2+6
18.4.8 5
三、解答题
19.∵四边形ABCD是平行四边形,∴OA=AC=6,OB=BD=9.∵OA+OB+AB=23,∴AB=23-6-9=8.
20.∵在△ADE中,AE=AD,∠ADE=75°,∴∠AED=75°(等边对等角),∴∠EAD=180°-75°×2=30°,又∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴△ABE中,AB=AE,∠BAE=120°∴∠AEB=(180°-120°)=30°.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23.(1)∠2=55°,∠3=70°;(2)
24.(1)解:由题意可得:,
∵,,,
∴,
∵点D为的中点,
∴,
过点P作PH⊥AB于点H,如图所示:
∵,
∴,
∴,
在Rt△AHP中,,
∴,
∴在Rt△PHD中,;
(2)证明:∵点Q运动至点B时,四边形是平行四边形,
∴PE∥BD,PE=BD,
∵点D为的中点,
∴,
∴PE∥AD,PE=AD,
∴四边形是平行四边形,
∴;
(3)由题意得:,
∵,,,
∴,
当点E恰好落在的边上时,则可分:
①当点E恰好落在的边上时,如图,
∵四边形是平行四边形,
∴PE=DQ,PD=QE,DQ∥AC,
∵∠ACB=90°,
∴,
∵点D为的中点,
∴,
∴,
∴,
∴,即;
②当点E恰好落在的边上时,如图,过点D、E分别作DN⊥BC,EM⊥AC,垂足分别为N、M,
∴,
∵四边形PEQD是平行四边形,
∴,
∴,
∵点D为的中点,
∴,
∴CN=BN,
∴,
由(1)得:,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴在Rt△CME中,,
∵,
∴,
解得:;
由题意可知点E恰好落在的边上是不存在的,
综上所述:当点E恰好落在的边上时,t的值为或.
D
A
C
B
F
E
题
C
A
B
┅┅
