人教版七年级数学 下册 9.1.1 不等式及其解集 课件(共31张)
文档属性
| 名称 | 人教版七年级数学 下册 9.1.1 不等式及其解集 课件(共31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
1.含有“=”的式子叫做等式;
2. 使等式两边相等的x的值称为方程的解;
3. 求方程的解的过程叫做解方程.
等式与方程
知识回顾
问题:五一期间,武汉市客车与火车免票规定:1米以下儿童免票;1米至1.4米的儿童半票.
x < 1
“1米以下”
你能用一个
数学式子
表示吗
设儿童
身高
为x米
9.1.1 不等式及其解集
人教版七年级数学 下册
目标导航
1.了解不等式及其解的概念;
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.(难点)
3.理解不等式的解集及解不等式的意义.(重点)
现实世界中存在大量的数量关系,包括相等关系和不等关系。用等式(包括方程),我们可以研究相等关系,而研究不等关系需要用本章的不等式,如引言中选择购物商场问题.
目标导学一:不等式的概念
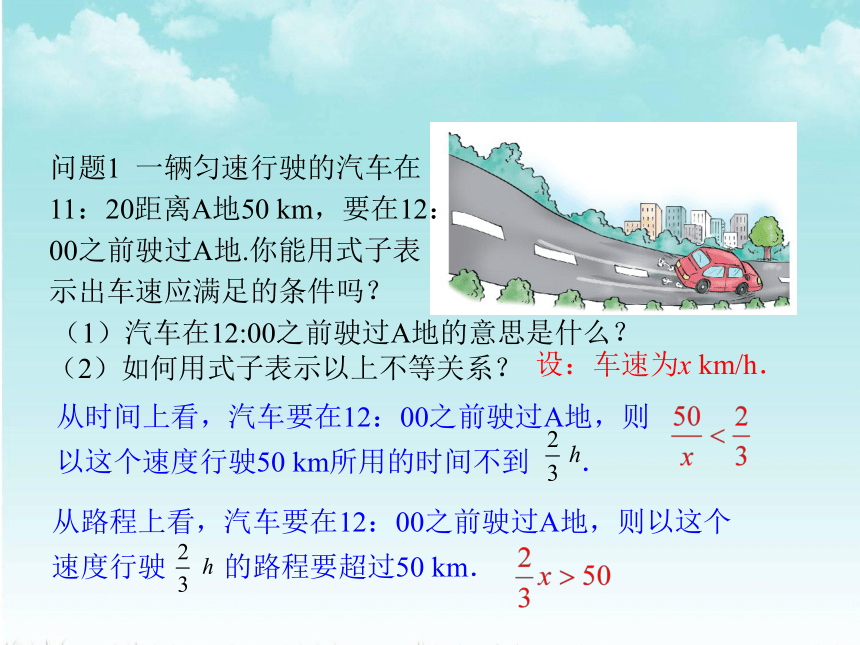
问题1 一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
(1)汽车在12:00之前驶过A地的意思是什么?
(2)如何用式子表示以上不等关系?
从时间上看,汽车要在12:00之前驶过A地,则
以这个速度行驶50 km所用的时间不到 .
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶 的路程要超过50 km.
设:车速为x km/h.
用符号“<”(或“≤”),“>”(或“≥”),“≠”连接而成的数学式子叫做不等式.
这些用来连接的符号统称不等号.
“≥”读作“大于或等于”或“不小于”
“≤”读作“小于或等于”或“不大于”
知识要点
判断下列各式是不是不等式。
2﹤5; ② x+3≠0;
③ 4x-2y≤0 ; ④ 7n-5≥2;
⑤3x+2>0 ; ⑥ 5m+3=8 .
否
是
是
是
是
是
练一练
例1 用不等式表示下列数量关系:
(1)x的5倍大于-7;
(2)a与b的和的一半小于-1;
(3)长、宽分别为xcm,ycm的长方形的面积小于
边长为acm的正方形的面积.
合作与交流
5x >-7
xy < a2
目标导学二:用不等式表示数量关系
交流:下面给出的数中,能使不等式x>50成立吗?你还能找出其他的数吗?
20, 40, 50, 100.
当x=20,20<50, 不成立;
当x=40,40<50, 不成立;
当x=50,50=50, 不成立;
当x=100,100>50, 成立.
解
目标导学三:不等式的解与解集
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似 , 能使不等式成立的未知数的值叫不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
例如:100是x>50的解.
概念学习
下列数中哪些是不等式x+3>6的解?
哪些不是。
-4 ,-2.5 ,0 ,1 ,2.5 ,3 ,3.2 ,
4.8 , 8 ,12。
√
√
√
√
一般的,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
想一想:
1.不等式的解和不等式的解集是一样的吗
2.不等式的解与解不等式一样吗?
求不等式的解集的过程叫解不等式.
概念学习
概念区分
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中
的一员
解集一定包括了
某个解
不等式的解与不等式的解集的区别与联系
直接说出下列不等式的解集:
(1) x+3 > 6;
(2) 2x < 8;
(3) x-2 > 0.
练一练
(1) x>3; (2) x<4; (3) x>2.
解:
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
问题1 如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
目标导学四:在数轴上表示不等式的解集
不等式的解集的表示方法
文字语言
数学式子
数轴表示
x <10
小于10的数
5
0
10
20
15
用数轴,一般标出数轴上某一区间,其中的
点对应的数值都是不等式的解.
用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 ; (2) x< .
0
-1
0
1
变式:
已知x的解集在数轴上表示如图,你能写出x的
解集吗
0
-2
x<-2
表示-1的点
表示 的点
方向向右
方向向左
空心圆圈表示不含此点
如图所示,x≤a
如图所示,x≥a
如图所示,x>a
如图所示,x<a
对于一元一次不等式的解集一般来说有
以下四种情况:
【例2】在数轴上表示下列不等式的解集
(1) x>-1; (2) x≥-1; (3) x<-1; (4) x≤-1
【解析】按画数轴,定界点,走方向的步骤答
解:如图
(1)x > 3
(2)x <4
(3)x>2
解:
例3 直接说出不等式的解集,并在数轴上表示出来.
(1)x+3 >6 ; (2)2x<8 ; (3)x-2 > 0 。
0
4
○
0
3
○
0
2
○
5.将下列不等式用数轴表示出来:
-4 -3 -2 -1 0 1
-1 0 1 2 3 4 5
x≥-3
x>2
x <4
3
0 1 2
练一练
1.不等式:
用符号“>”或“<”表示大小关系的式子.
2.不等式的解:
能使不等式成立的未知数的值.
4.解不等式:
求不等式的解集的过程.
3.不等式的解集:
使不等式成立的未知数的取值范围.
5.解集表示方式:
①不等式;
②数轴.
课堂小结
1、判断下列式子是不是不等式:
(1)-3>0; (2)4x+3y<0;
(3)x=3; (4) x2+xy+y2;
(5)x≠5; (6)x+2>y+5.
解 : (1)(2)(5)(6)是不等式;
(3)(4)不是不等式.
检测目标
2、用不等式表示:
(1)a是正数; (2)a是负数;
(3) a与5的和小于7; (4)a与2的差大于-1;
(5)a的4倍大于8; (6)a的一半小于3.
解:
(1)a>0; (2)a<0;
(3)a+5<7; (4)a-2>-1;
(5)4a>8; (6) a<3.
检测目标
3.下列说法中错误的是( )
A.不等式x<5的解有无数个
B.不等式x<5的正整数解有有限个
C.x=-4是不等式-3x>9的一个解
D.x>5是不等式x+3>6的解集
D
检测目标
4、奥运射箭比赛,每一箭满分为10分. 某选手在参加比赛时,前十箭中最低得分为7分,求该选手前十箭总得分x的范围。
解:
检测目标
画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 (2)x<
0
-1
1
0
1
2
变 式: 已知x的取值范围如图所示,你能写出x的取值范围吗
0
-1
-2
x<-2
检测目标
通过本课学习,你收获了什么?
1.含有“=”的式子叫做等式;
2. 使等式两边相等的x的值称为方程的解;
3. 求方程的解的过程叫做解方程.
等式与方程
知识回顾
问题:五一期间,武汉市客车与火车免票规定:1米以下儿童免票;1米至1.4米的儿童半票.
x < 1
“1米以下”
你能用一个
数学式子
表示吗
设儿童
身高
为x米
9.1.1 不等式及其解集
人教版七年级数学 下册
目标导航
1.了解不等式及其解的概念;
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.(难点)
3.理解不等式的解集及解不等式的意义.(重点)
现实世界中存在大量的数量关系,包括相等关系和不等关系。用等式(包括方程),我们可以研究相等关系,而研究不等关系需要用本章的不等式,如引言中选择购物商场问题.
目标导学一:不等式的概念
问题1 一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
(1)汽车在12:00之前驶过A地的意思是什么?
(2)如何用式子表示以上不等关系?
从时间上看,汽车要在12:00之前驶过A地,则
以这个速度行驶50 km所用的时间不到 .
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶 的路程要超过50 km.
设:车速为x km/h.
用符号“<”(或“≤”),“>”(或“≥”),“≠”连接而成的数学式子叫做不等式.
这些用来连接的符号统称不等号.
“≥”读作“大于或等于”或“不小于”
“≤”读作“小于或等于”或“不大于”
知识要点
判断下列各式是不是不等式。
2﹤5; ② x+3≠0;
③ 4x-2y≤0 ; ④ 7n-5≥2;
⑤3x+2>0 ; ⑥ 5m+3=8 .
否
是
是
是
是
是
练一练
例1 用不等式表示下列数量关系:
(1)x的5倍大于-7;
(2)a与b的和的一半小于-1;
(3)长、宽分别为xcm,ycm的长方形的面积小于
边长为acm的正方形的面积.
合作与交流
5x >-7
xy < a2
目标导学二:用不等式表示数量关系
交流:下面给出的数中,能使不等式x>50成立吗?你还能找出其他的数吗?
20, 40, 50, 100.
当x=20,20<50, 不成立;
当x=40,40<50, 不成立;
当x=50,50=50, 不成立;
当x=100,100>50, 成立.
解
目标导学三:不等式的解与解集
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似 , 能使不等式成立的未知数的值叫不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
例如:100是x>50的解.
概念学习
下列数中哪些是不等式x+3>6的解?
哪些不是。
-4 ,-2.5 ,0 ,1 ,2.5 ,3 ,3.2 ,
4.8 , 8 ,12。
√
√
√
√
一般的,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
想一想:
1.不等式的解和不等式的解集是一样的吗
2.不等式的解与解不等式一样吗?
求不等式的解集的过程叫解不等式.
概念学习
概念区分
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中
的一员
解集一定包括了
某个解
不等式的解与不等式的解集的区别与联系
直接说出下列不等式的解集:
(1) x+3 > 6;
(2) 2x < 8;
(3) x-2 > 0.
练一练
(1) x>3; (2) x<4; (3) x>2.
解:
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
问题1 如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
目标导学四:在数轴上表示不等式的解集
不等式的解集的表示方法
文字语言
数学式子
数轴表示
x <10
小于10的数
5
0
10
20
15
用数轴,一般标出数轴上某一区间,其中的
点对应的数值都是不等式的解.
用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 ; (2) x< .
0
-1
0
1
变式:
已知x的解集在数轴上表示如图,你能写出x的
解集吗
0
-2
x<-2
表示-1的点
表示 的点
方向向右
方向向左
空心圆圈表示不含此点
如图所示,x≤a
如图所示,x≥a
如图所示,x>a
如图所示,x<a
对于一元一次不等式的解集一般来说有
以下四种情况:
【例2】在数轴上表示下列不等式的解集
(1) x>-1; (2) x≥-1; (3) x<-1; (4) x≤-1
【解析】按画数轴,定界点,走方向的步骤答
解:如图
(1)x > 3
(2)x <4
(3)x>2
解:
例3 直接说出不等式的解集,并在数轴上表示出来.
(1)x+3 >6 ; (2)2x<8 ; (3)x-2 > 0 。
0
4
○
0
3
○
0
2
○
5.将下列不等式用数轴表示出来:
-4 -3 -2 -1 0 1
-1 0 1 2 3 4 5
x≥-3
x>2
x <4
3
0 1 2
练一练
1.不等式:
用符号“>”或“<”表示大小关系的式子.
2.不等式的解:
能使不等式成立的未知数的值.
4.解不等式:
求不等式的解集的过程.
3.不等式的解集:
使不等式成立的未知数的取值范围.
5.解集表示方式:
①不等式;
②数轴.
课堂小结
1、判断下列式子是不是不等式:
(1)-3>0; (2)4x+3y<0;
(3)x=3; (4) x2+xy+y2;
(5)x≠5; (6)x+2>y+5.
解 : (1)(2)(5)(6)是不等式;
(3)(4)不是不等式.
检测目标
2、用不等式表示:
(1)a是正数; (2)a是负数;
(3) a与5的和小于7; (4)a与2的差大于-1;
(5)a的4倍大于8; (6)a的一半小于3.
解:
(1)a>0; (2)a<0;
(3)a+5<7; (4)a-2>-1;
(5)4a>8; (6) a<3.
检测目标
3.下列说法中错误的是( )
A.不等式x<5的解有无数个
B.不等式x<5的正整数解有有限个
C.x=-4是不等式-3x>9的一个解
D.x>5是不等式x+3>6的解集
D
检测目标
4、奥运射箭比赛,每一箭满分为10分. 某选手在参加比赛时,前十箭中最低得分为7分,求该选手前十箭总得分x的范围。
解:
检测目标
画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 (2)x<
0
-1
1
0
1
2
变 式: 已知x的取值范围如图所示,你能写出x的取值范围吗
0
-1
-2
x<-2
检测目标
通过本课学习,你收获了什么?
