5.1.1 相交线 课件(共24张PPT)
文档属性
| 名称 | 5.1.1 相交线 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
第五章
相交线与平行线
七年级数学人教版·下册
5.1.1 相交线
授课人:XXXX
教学目标
1.对顶角的性质;(重点)
2.理解对顶角相等的性质的探索.(难点)
新课导入
这里有一把剪刀, 握紧剪刀的把手, 就能剪开物体, 你能说出其中的道理吗?
新课导入
如果把剪子的构造抽象成一个几何图形, 会是什么样的图形?
新课导入
仔细观察你所画的图形, 当两条直线相交时, 所形成的四个角中, ∠1与∠2有怎样的位置关系?
∠1与∠2的顶点所在的位置有什么特点?
有一个公共顶点O.
A
B
C
D
O
1
2
3
4
新课导入
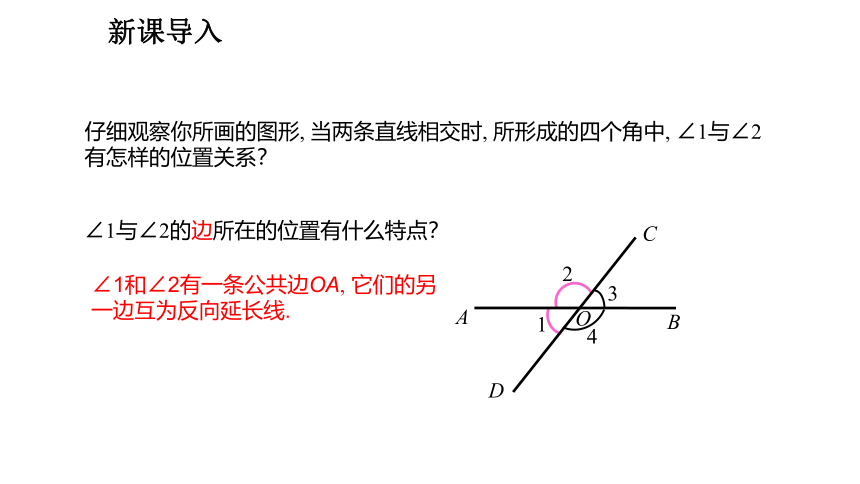
仔细观察你所画的图形, 当两条直线相交时, 所形成的四个角中, ∠1与∠2有怎样的位置关系?
∠1与∠2的边所在的位置有什么特点?
∠1和∠2有一条公共边OA, 它们的另一边互为反向延长线.
A
B
C
D
O
1
2
3
4
知识归纳
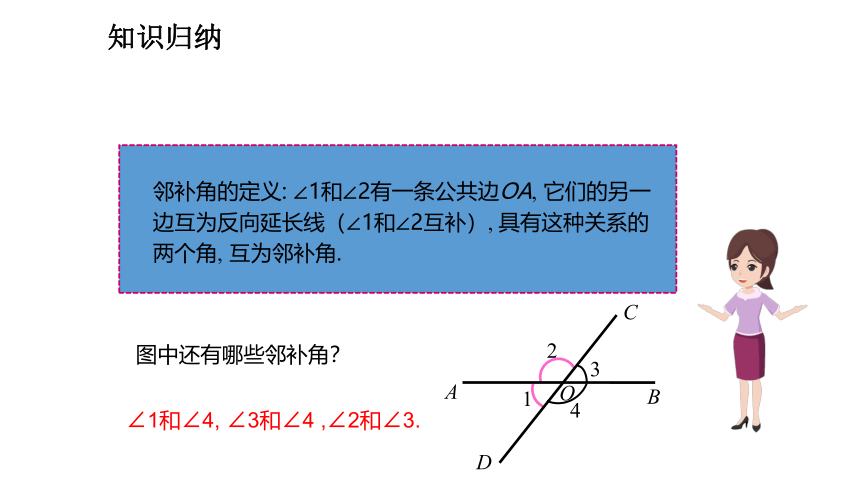
邻补角的定义: ∠1和∠2有一条公共边OA, 它们的另一边互为反向延长线(∠1和∠2互补), 具有这种关系的两个角, 互为邻补角.
图中还有哪些邻补角?
∠1和∠4, ∠3和∠4 ,∠2和∠3.
A
B
C
D
O
1
2
3
4
新知探究
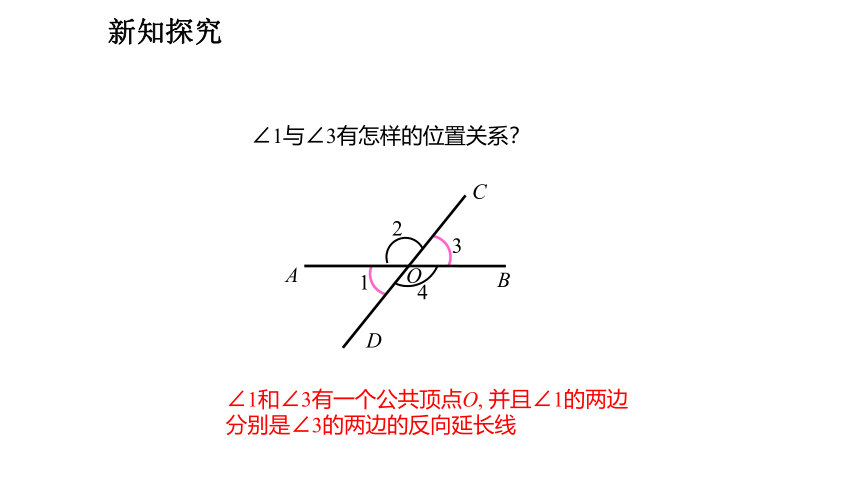
∠1与∠3有怎样的位置关系?
∠1和∠3有一个公共顶点O, 并且∠1的两边分别是∠3的两边的反向延长线
A
B
C
D
O
1
2
3
4
知识归纳
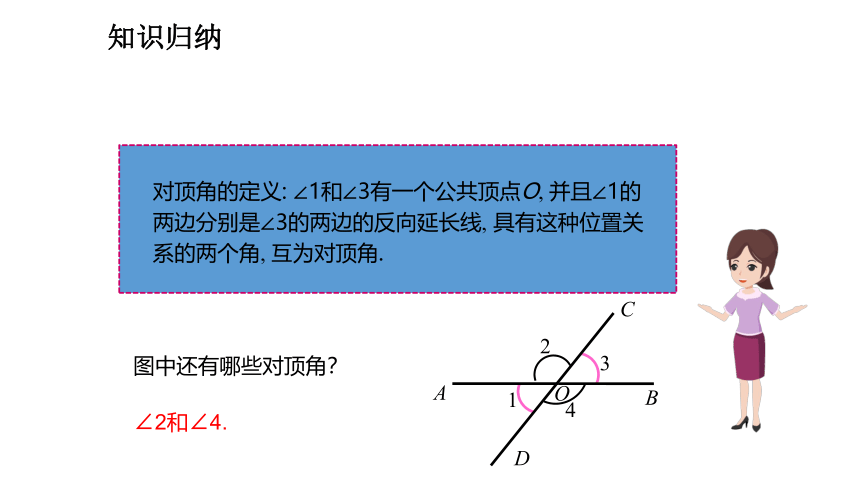
对顶角的定义: ∠1和∠3有一个公共顶点O, 并且∠1的两边分别是∠3的两边的反向延长线, 具有这种位置关系的两个角, 互为对顶角.
∠2和∠4.
图中还有哪些对顶角?
A
B
C
D
O
1
2
3
4
新知探究
例 1:(1)下列各图中, ∠1和∠2是邻补角吗?
(1) (2) (3)
1
2
1
1
2
2
新知探究
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
例1:(2)下列各图中, ∠1和∠2是对顶角吗?
新知探究
例1: (3)如图, 三条直线 AB , CD , EF相交于点O, ∠AOE的对顶角是 , ∠EOD的邻补角是 .
A
B
F
C
D
E
∠FOB
∠FOD,
∠COE
O
知识归纳
对顶角的性质: 对顶角相等
你能说出∠1=∠3的道理吗?
因为 ∠1与∠2 互补,
∠3与∠2 互补(邻补角的定义),
所以 ∠1=∠3(同角的补角相等),
同理 ∠2=∠4.
请你用数学的语言写出这个过程.
A
B
C
D
O
1
2
3
4
新知探究
例2: 如图, 直线a, b相交于点O, ∠1= , 求∠2 , ∠3 , ∠4 的度数.
1
2
3
4
a
b
O
解:由邻补角的定义, 得
∠2=180°-∠1=180°-40°=140°.
由对顶角相等, 得
∠3=∠1=40°,∠4=∠2=140°.
新知探究
例3: 如图, 直线 AB与CD相交于点O, OD恰为∠BOE的角平分线.
(1)请直接写出和∠AOD互为补角的角(把符合条件的角都写出来).
(2)若∠AOD=142°, 求∠AOE的度数.
解:(1)∠AOC, ∠BOD, ∠EOD.
(2)∵∠AOD=142°,
∴∠BOD=38°.
∵OD为∠BOE的角平分线,
∴∠EOD=38°,
∴∠AOE=∠AOD-∠EOD=142°-38°=104°.
1. 如图, 直线AB和CD相交于点O, 则∠AOC的邻补角是 ,
∠AOD 的邻补角是 .
∠AOD, ∠COB
∠AOC, ∠DOB
新知探究
2. 如图, 直线 AB, CD, EF 相交于点O, 则∠1+∠2+∠3等于 ( )
A. 90° B. 120° C. 180° D. 不能确定
C
新知探究
课堂小结
相交线
邻补角定义.
对顶角定义,对顶角相等.
课堂小测
1. 下列各组角中, ∠1与∠2是对顶角的为 ( )
D
课堂小测
2.已知如图, 直线AB, CD相交于点O, ∠AOC=60°, OE把∠BOD分成两部分,
且∠BOE: ∠EOD=1: 2, 则∠AOE 等于 ( )
A. 180° B. 160° C. 140° D. 120°
B
课堂小测
3. 如图, 三条直线l1, l2, l3相交于点E, ∠1=30°, 则∠2+∠3= ( )
A. 90° B. 120° C. 150° D. 180°
C
课堂小测
4. 如图, 已知∠1+∠3=180°, 则图中与∠1互补的角有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
D
课堂小测
5.如图, 直线 AB, CD 相交于O点, 若∠1=30°, 求∠2, ∠3的度数.
解: 因为∠1与∠3是对顶角,
所以∠3=∠1=30°.
因为∠1与∠2是邻补角,
即∠1+∠2=180°,
所以∠2=180°-30°=150°.
第五章
相交线与平行线
七年级数学人教版·下册
5.1.1 相交线
授课人:XXXX
教学目标
1.对顶角的性质;(重点)
2.理解对顶角相等的性质的探索.(难点)
新课导入
这里有一把剪刀, 握紧剪刀的把手, 就能剪开物体, 你能说出其中的道理吗?
新课导入
如果把剪子的构造抽象成一个几何图形, 会是什么样的图形?
新课导入
仔细观察你所画的图形, 当两条直线相交时, 所形成的四个角中, ∠1与∠2有怎样的位置关系?
∠1与∠2的顶点所在的位置有什么特点?
有一个公共顶点O.
A
B
C
D
O
1
2
3
4
新课导入
仔细观察你所画的图形, 当两条直线相交时, 所形成的四个角中, ∠1与∠2有怎样的位置关系?
∠1与∠2的边所在的位置有什么特点?
∠1和∠2有一条公共边OA, 它们的另一边互为反向延长线.
A
B
C
D
O
1
2
3
4
知识归纳
邻补角的定义: ∠1和∠2有一条公共边OA, 它们的另一边互为反向延长线(∠1和∠2互补), 具有这种关系的两个角, 互为邻补角.
图中还有哪些邻补角?
∠1和∠4, ∠3和∠4 ,∠2和∠3.
A
B
C
D
O
1
2
3
4
新知探究
∠1与∠3有怎样的位置关系?
∠1和∠3有一个公共顶点O, 并且∠1的两边分别是∠3的两边的反向延长线
A
B
C
D
O
1
2
3
4
知识归纳
对顶角的定义: ∠1和∠3有一个公共顶点O, 并且∠1的两边分别是∠3的两边的反向延长线, 具有这种位置关系的两个角, 互为对顶角.
∠2和∠4.
图中还有哪些对顶角?
A
B
C
D
O
1
2
3
4
新知探究
例 1:(1)下列各图中, ∠1和∠2是邻补角吗?
(1) (2) (3)
1
2
1
1
2
2
新知探究
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
例1:(2)下列各图中, ∠1和∠2是对顶角吗?
新知探究
例1: (3)如图, 三条直线 AB , CD , EF相交于点O, ∠AOE的对顶角是 , ∠EOD的邻补角是 .
A
B
F
C
D
E
∠FOB
∠FOD,
∠COE
O
知识归纳
对顶角的性质: 对顶角相等
你能说出∠1=∠3的道理吗?
因为 ∠1与∠2 互补,
∠3与∠2 互补(邻补角的定义),
所以 ∠1=∠3(同角的补角相等),
同理 ∠2=∠4.
请你用数学的语言写出这个过程.
A
B
C
D
O
1
2
3
4
新知探究
例2: 如图, 直线a, b相交于点O, ∠1= , 求∠2 , ∠3 , ∠4 的度数.
1
2
3
4
a
b
O
解:由邻补角的定义, 得
∠2=180°-∠1=180°-40°=140°.
由对顶角相等, 得
∠3=∠1=40°,∠4=∠2=140°.
新知探究
例3: 如图, 直线 AB与CD相交于点O, OD恰为∠BOE的角平分线.
(1)请直接写出和∠AOD互为补角的角(把符合条件的角都写出来).
(2)若∠AOD=142°, 求∠AOE的度数.
解:(1)∠AOC, ∠BOD, ∠EOD.
(2)∵∠AOD=142°,
∴∠BOD=38°.
∵OD为∠BOE的角平分线,
∴∠EOD=38°,
∴∠AOE=∠AOD-∠EOD=142°-38°=104°.
1. 如图, 直线AB和CD相交于点O, 则∠AOC的邻补角是 ,
∠AOD 的邻补角是 .
∠AOD, ∠COB
∠AOC, ∠DOB
新知探究
2. 如图, 直线 AB, CD, EF 相交于点O, 则∠1+∠2+∠3等于 ( )
A. 90° B. 120° C. 180° D. 不能确定
C
新知探究
课堂小结
相交线
邻补角定义.
对顶角定义,对顶角相等.
课堂小测
1. 下列各组角中, ∠1与∠2是对顶角的为 ( )
D
课堂小测
2.已知如图, 直线AB, CD相交于点O, ∠AOC=60°, OE把∠BOD分成两部分,
且∠BOE: ∠EOD=1: 2, 则∠AOE 等于 ( )
A. 180° B. 160° C. 140° D. 120°
B
课堂小测
3. 如图, 三条直线l1, l2, l3相交于点E, ∠1=30°, 则∠2+∠3= ( )
A. 90° B. 120° C. 150° D. 180°
C
课堂小测
4. 如图, 已知∠1+∠3=180°, 则图中与∠1互补的角有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
D
课堂小测
5.如图, 直线 AB, CD 相交于O点, 若∠1=30°, 求∠2, ∠3的度数.
解: 因为∠1与∠3是对顶角,
所以∠3=∠1=30°.
因为∠1与∠2是邻补角,
即∠1+∠2=180°,
所以∠2=180°-30°=150°.
