5.1.2 垂线 课件(共22张PPT)
图片预览




文档简介
(共22张PPT)
第五章
相交线与平行线
七年级数学人教版·下册
5.1.2 垂线
授课人:XXXX
教学目标
1.垂线、垂线段、点到直线的距离的概念;(重点)
2.垂线的性质和点到直线的距离.(难点)
新课导入
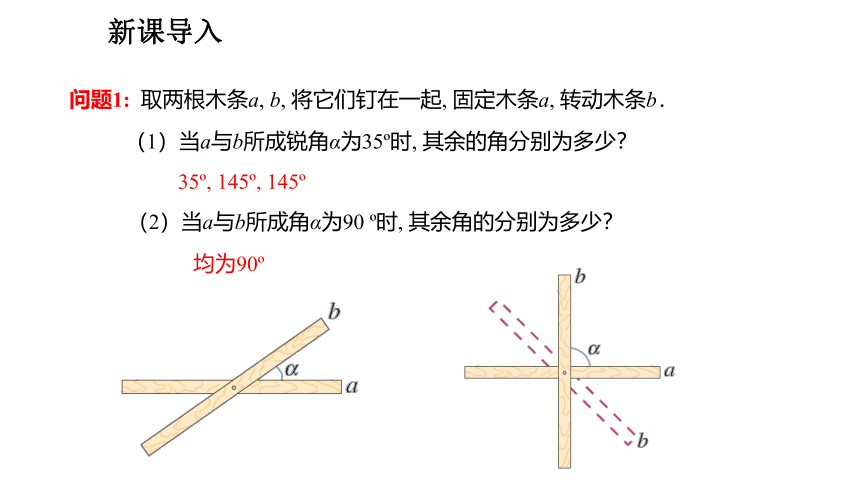
问题1: 取两根木条a, b, 将它们钉在一起, 固定木条a, 转动木条b.
(2)当a与b所成角α为90 时, 其余角的分别为多少?
35 , 145 , 145
均为90
(1)当a与b所成锐角α为35 时, 其余的角分别为多少?
新课导入
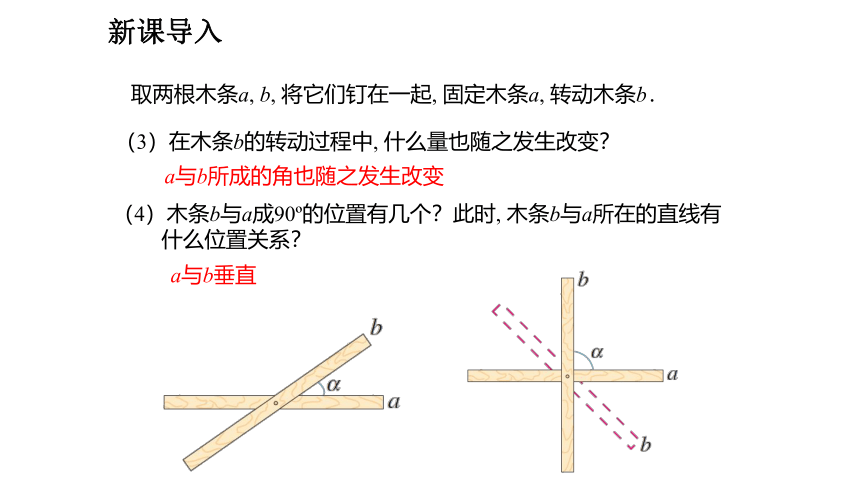
取两根木条a, b, 将它们钉在一起, 固定木条a, 转动木条b.
(3)在木条b的转动过程中, 什么量也随之发生改变?
(4)木条b与a成90 的位置有几个?此时, 木条b与a所在的直线有
什么位置关系?
a与b所成的角也随之发生改变
a与b垂直
知识归纳
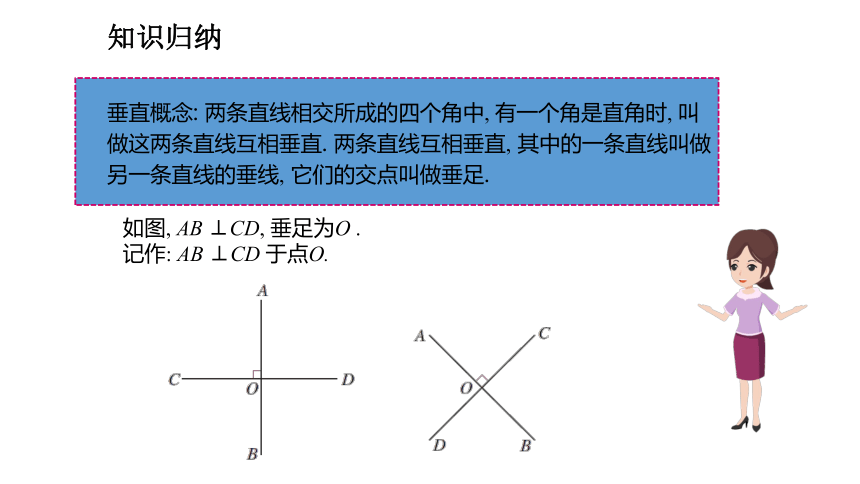
垂直概念: 两条直线相交所成的四个角中, 有一个角是直角时, 叫做这两条直线互相垂直. 两条直线互相垂直, 其中的一条直线叫做另一条直线的垂线, 它们的交点叫做垂足.
如图, AB ⊥CD, 垂足为O .
记作: AB ⊥CD 于点O.
新知探究
问题2:(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内, 两条直线的位置关系有3种: 相交, 平行, 垂直?
垂直是相交的特殊情况.
不能, 因为垂直是相交的特殊情况.
(3)如何判定两条射线垂直?两条线段呢?
(4)你能举出一些生活中与垂直有关的实例吗?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直, 都是指它们所在的直线垂直.
新知探究
问题3: 用三角尺或量角器画已知直线 l 的垂线.
(1)用三角尺或量角器画已知直线 l 的垂线, 这样的垂线能画出几条?
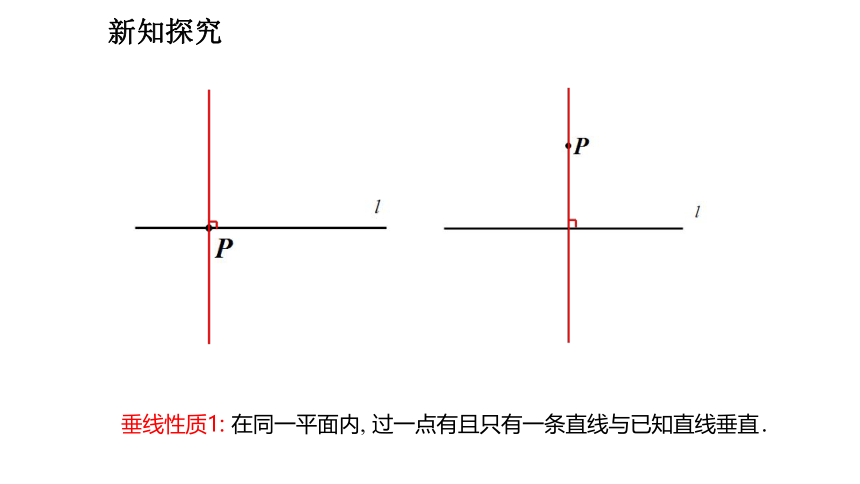
(2)经过一点画已知直线 l 的垂线, 这样的垂线能画出几条?
①经过一点画已知直线 l 的垂线有几种情况?
②通过画图, 你发现过一个点可以画几条直线与已知直线垂直?
无数条
新知探究
垂线性质1: 在同一平面内, 过一点有且只有一条直线与已知直线垂直.
新知探究
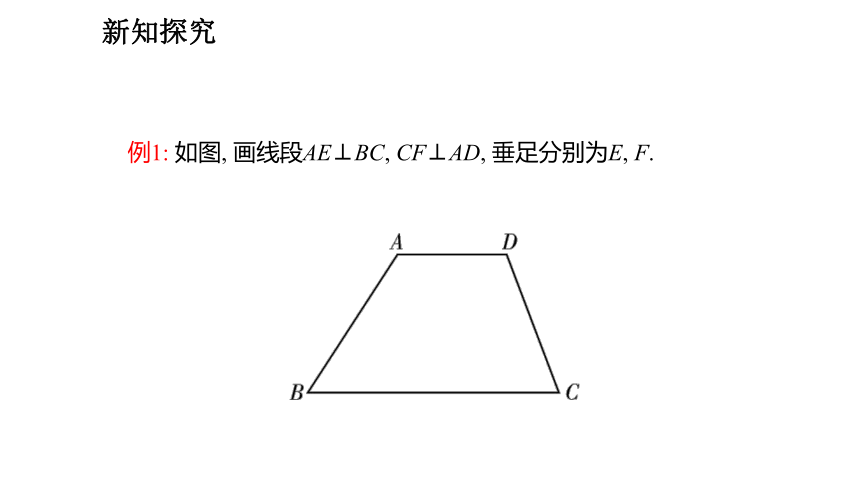
例1: 如图, 画线段AE⊥BC, CF⊥AD, 垂足分别为E, F.
新知探究
解: 如图, 线段 AE, CF 即为所求.
新知探究
过点P画出射线AB或线段AB的垂线.
新知探究
思考:(1)图中哪条线段垂直于直线 l
(2)观察和测量, 线段PO, PA1, PA2, PA3中哪条线段最长
(3)继续比较, PAm和PAm+1哪条线段长
(4)上述的线段都是在垂线PO的左侧, 在垂线PO的右侧也有这个结论吗
(5)从上述比较中,你发现了什么结论
线段PO.
线段PA3.
线段PAm+1.
有这个结论.
知识归纳
垂线性质2: 连接直线外一点与直线上各点的所有线段中, 垂线段最短.
简单说成: 垂线段最短.
点到直线的距离: 直线外一点到这条直线的垂线段的长度, 叫点到直线的距离.
新知探究
例2: 如图, 要把河中的水引到水池A中, 应在河岸B处(AB⊥CD)开始
挖渠才能使水渠的长度最短, 这样做依据的几何学原理是 ( )
A. 两点之间线段最短
B. 点到直线的距离
C. 两点确定一条直线
D. 垂线段最短
D
新知探究
例3: 如图所示, 已知∠BAC=90°, AD⊥BC于点D, 给出以下结论:
①点B到AC的垂线段就是线段AB; ②AB, AD, AC三条线段中, 线段 AD
最短; ③点A到BC的距离就是线段AD的长度; ④点C和点B的距离就是
线段CA的长度. 其中正确结论共有 ( )
A. 4个 B. 3个 C. 2个 D. 1个
B
课堂小结
垂线
垂直定义:两条直线相交所成的四个角中, 有一个角是直角时, 叫做这两条直线互相垂直. 两条直线互相垂直, 其中的一条直线叫做另一条直线的垂线, 它们的交点叫做垂足.
垂线性质1:在同一平面内, 过一点有且只有一条直线与已知直线垂直.
垂线性质2:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度, 叫点到直线的距离.
课堂小测
1.已知∠α 的两边分别与∠β 的两边垂直, 且∠α=20°, 则∠β 的度数为 ( )
A. 20° B. 160° C.20°或160° D. 70°
C
2.如图, 直线AB与直线CD相交于点O, OE⊥AB, 垂足为O, ∠EOD= ∠AOC, 则
∠BOC等于 ( )
A. 150° B. 140° C. 130° D. 120°
D
课堂小测
3.如图, 直线AB, CD相交于点O, ∠AOC=60°, OE 把∠BOD 分成两部分,
且∠BOE : ∠EOD=1: 2, 则∠AOE 等于 ( )
A. 180° B. 160° C. 140° D. 120°
B
课堂小测
4.如图, 平面上有 A, B, C 三点.
(1)作直线AB, 作射线 BC (不写作法, 下同);
(2)过点 A 作射线 BC 的垂线, 垂足为G; 过点 A 作直线AB的垂线, 交射线 BC 于点 H.
解:(1)(2)如图所示.
课堂小测
5.如图, 已知OC⊥AB于点O, ∠AOD :∠COD =1: 2. (1)若OE平分∠BOC, 求∠DOE的度数; (2)若∠AOE 的度数比∠COE 的度数的3倍多30°, 试判断
OD 与OE 的位置关系, 并说明理由.
解: (1)因为OC⊥AB于点O,
所以∠AOC=∠BOC=90°.
因为∠AOC=90°,∠AOD :∠COD=1: 2,
所以∠DOC=60°.
因为OE平分∠BOC,∠BOC=90°,
所以∠COE=45°,
所以∠DOE=∠DOC+∠COE=60°+45°=105°.
课堂小测
(2)OD⊥OE. 理由如下:
因为OC⊥AB于点O,
所以∠AOC=∠BOC=90°.
因为∠AOC=90°,∠AOD : ∠COD=1: 2,
所以∠DOC=60°.
因为∠AOE-∠COE=2∠COE+30°,
且∠AOE-∠COE=90°,
所以2∠COE+30°=90°, 所以∠COE=30°.
因为∠DOE=∠DOC+∠COE=60°+30°=90°,
所以OD⊥OE.
A
O
B
C
D
E
第五章
相交线与平行线
七年级数学人教版·下册
5.1.2 垂线
授课人:XXXX
教学目标
1.垂线、垂线段、点到直线的距离的概念;(重点)
2.垂线的性质和点到直线的距离.(难点)
新课导入
问题1: 取两根木条a, b, 将它们钉在一起, 固定木条a, 转动木条b.
(2)当a与b所成角α为90 时, 其余角的分别为多少?
35 , 145 , 145
均为90
(1)当a与b所成锐角α为35 时, 其余的角分别为多少?
新课导入
取两根木条a, b, 将它们钉在一起, 固定木条a, 转动木条b.
(3)在木条b的转动过程中, 什么量也随之发生改变?
(4)木条b与a成90 的位置有几个?此时, 木条b与a所在的直线有
什么位置关系?
a与b所成的角也随之发生改变
a与b垂直
知识归纳
垂直概念: 两条直线相交所成的四个角中, 有一个角是直角时, 叫做这两条直线互相垂直. 两条直线互相垂直, 其中的一条直线叫做另一条直线的垂线, 它们的交点叫做垂足.
如图, AB ⊥CD, 垂足为O .
记作: AB ⊥CD 于点O.
新知探究
问题2:(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内, 两条直线的位置关系有3种: 相交, 平行, 垂直?
垂直是相交的特殊情况.
不能, 因为垂直是相交的特殊情况.
(3)如何判定两条射线垂直?两条线段呢?
(4)你能举出一些生活中与垂直有关的实例吗?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直, 都是指它们所在的直线垂直.
新知探究
问题3: 用三角尺或量角器画已知直线 l 的垂线.
(1)用三角尺或量角器画已知直线 l 的垂线, 这样的垂线能画出几条?
(2)经过一点画已知直线 l 的垂线, 这样的垂线能画出几条?
①经过一点画已知直线 l 的垂线有几种情况?
②通过画图, 你发现过一个点可以画几条直线与已知直线垂直?
无数条
新知探究
垂线性质1: 在同一平面内, 过一点有且只有一条直线与已知直线垂直.
新知探究
例1: 如图, 画线段AE⊥BC, CF⊥AD, 垂足分别为E, F.
新知探究
解: 如图, 线段 AE, CF 即为所求.
新知探究
过点P画出射线AB或线段AB的垂线.
新知探究
思考:(1)图中哪条线段垂直于直线 l
(2)观察和测量, 线段PO, PA1, PA2, PA3中哪条线段最长
(3)继续比较, PAm和PAm+1哪条线段长
(4)上述的线段都是在垂线PO的左侧, 在垂线PO的右侧也有这个结论吗
(5)从上述比较中,你发现了什么结论
线段PO.
线段PA3.
线段PAm+1.
有这个结论.
知识归纳
垂线性质2: 连接直线外一点与直线上各点的所有线段中, 垂线段最短.
简单说成: 垂线段最短.
点到直线的距离: 直线外一点到这条直线的垂线段的长度, 叫点到直线的距离.
新知探究
例2: 如图, 要把河中的水引到水池A中, 应在河岸B处(AB⊥CD)开始
挖渠才能使水渠的长度最短, 这样做依据的几何学原理是 ( )
A. 两点之间线段最短
B. 点到直线的距离
C. 两点确定一条直线
D. 垂线段最短
D
新知探究
例3: 如图所示, 已知∠BAC=90°, AD⊥BC于点D, 给出以下结论:
①点B到AC的垂线段就是线段AB; ②AB, AD, AC三条线段中, 线段 AD
最短; ③点A到BC的距离就是线段AD的长度; ④点C和点B的距离就是
线段CA的长度. 其中正确结论共有 ( )
A. 4个 B. 3个 C. 2个 D. 1个
B
课堂小结
垂线
垂直定义:两条直线相交所成的四个角中, 有一个角是直角时, 叫做这两条直线互相垂直. 两条直线互相垂直, 其中的一条直线叫做另一条直线的垂线, 它们的交点叫做垂足.
垂线性质1:在同一平面内, 过一点有且只有一条直线与已知直线垂直.
垂线性质2:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度, 叫点到直线的距离.
课堂小测
1.已知∠α 的两边分别与∠β 的两边垂直, 且∠α=20°, 则∠β 的度数为 ( )
A. 20° B. 160° C.20°或160° D. 70°
C
2.如图, 直线AB与直线CD相交于点O, OE⊥AB, 垂足为O, ∠EOD= ∠AOC, 则
∠BOC等于 ( )
A. 150° B. 140° C. 130° D. 120°
D
课堂小测
3.如图, 直线AB, CD相交于点O, ∠AOC=60°, OE 把∠BOD 分成两部分,
且∠BOE : ∠EOD=1: 2, 则∠AOE 等于 ( )
A. 180° B. 160° C. 140° D. 120°
B
课堂小测
4.如图, 平面上有 A, B, C 三点.
(1)作直线AB, 作射线 BC (不写作法, 下同);
(2)过点 A 作射线 BC 的垂线, 垂足为G; 过点 A 作直线AB的垂线, 交射线 BC 于点 H.
解:(1)(2)如图所示.
课堂小测
5.如图, 已知OC⊥AB于点O, ∠AOD :∠COD =1: 2. (1)若OE平分∠BOC, 求∠DOE的度数; (2)若∠AOE 的度数比∠COE 的度数的3倍多30°, 试判断
OD 与OE 的位置关系, 并说明理由.
解: (1)因为OC⊥AB于点O,
所以∠AOC=∠BOC=90°.
因为∠AOC=90°,∠AOD :∠COD=1: 2,
所以∠DOC=60°.
因为OE平分∠BOC,∠BOC=90°,
所以∠COE=45°,
所以∠DOE=∠DOC+∠COE=60°+45°=105°.
课堂小测
(2)OD⊥OE. 理由如下:
因为OC⊥AB于点O,
所以∠AOC=∠BOC=90°.
因为∠AOC=90°,∠AOD : ∠COD=1: 2,
所以∠DOC=60°.
因为∠AOE-∠COE=2∠COE+30°,
且∠AOE-∠COE=90°,
所以2∠COE+30°=90°, 所以∠COE=30°.
因为∠DOE=∠DOC+∠COE=60°+30°=90°,
所以OD⊥OE.
A
O
B
C
D
E
