2021-2022学年度人教版七年级数学下册课件 6.3.1 实数的概念 (共19张PPT)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学下册课件 6.3.1 实数的概念 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 14:28:16 | ||
图片预览





文档简介
(共19张PPT)
第六章
实数
七年级数学人教版·下册
6.3.1 实数的概念
授课人:XXXX
教学目标
1.正确理解实数的概念;(重点)
2.了解实数和数轴上的点一一对应, 能用数轴上的点
表示无理数.(难点)
有理数包括整数和分数, 如果将下列分数写成小数的形式, 你有什么发现?
整数能写成小数的形式吗?3可以看成是3.0吗?
它们都可以化成有限小数或无限循环小数的形式.
可以.
有理数都可化成有限小数或无限循环小数的形式.
反过来, 任何有限小数或无限循环小数也都是有理数.
新课导入
新课导入
我们学过的数是否都具有以上问题中数的特征?请举例说明.
不是.
它们都是无限不循环小数, 还是有理数吗?
知识归纳
无理数: 无限不循环小数.
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数, 如
1.01001000100001…
无理数的概念
新知探究
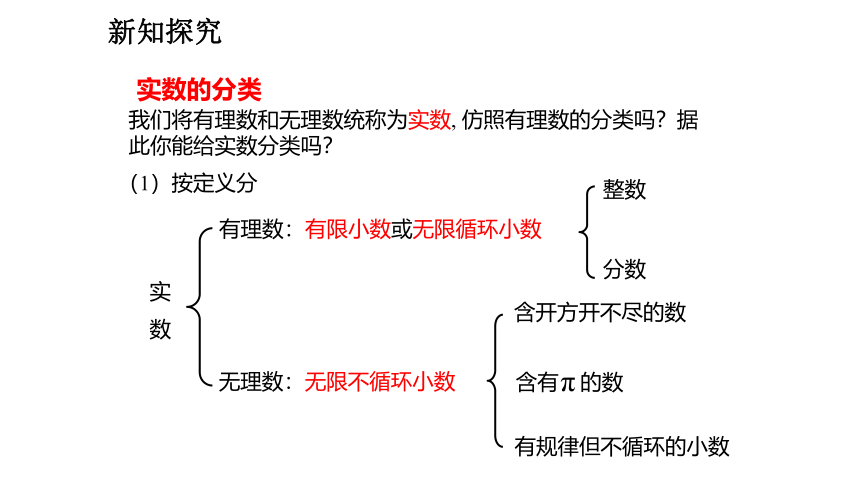
我们将有理数和无理数统称为实数, 仿照有理数的分类吗?据此你能给实数分类吗?
无理数:无限不循环小数
有理数:有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
实数的分类
新知探究
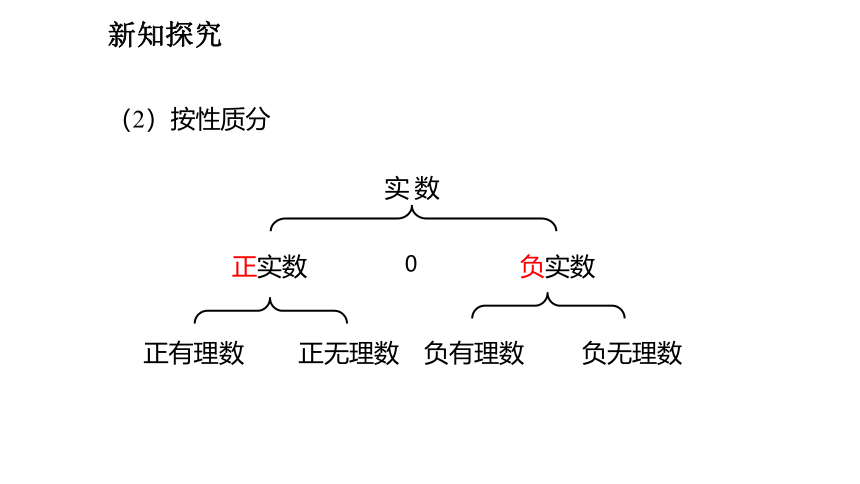
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
新知探究
无理数:
有理数:
正实数:
负实数:
例1: 将下列各数分别填入下列相应的括号内:
注意: 对每个数都要进行判断, 分类标准不同结果不同.
新知探究
思考1: 如图, 直径为1个单位长度的圆从原点沿数轴向右滚动一周, 圆上一点从原点到达A点, 则数轴上表示点A的数是多少
因为圆的周长为π, 无理数π可以用数轴上的点来表示.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
实数与数轴上的点
把两个边长为1的小正方形通过剪、拼, 得到一个大正方形, 大正方形的边长为 , 从而说明边长为1的小正方形的对角线为 .
新知探究
思考2: 你能在数轴上表示出 和 - 吗?
1
1
1
1
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来, 数轴上的每一点都表示一个实数.
实数和数轴上的点是一 一对应的.
新知探究
实数的大小比较
与有理数规定的大小一样, 数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零, 负数小于零, 正数大于负数;
2.两个正数, 绝对值大的数较大;
3.两个负数, 绝对值大的数反而小.
与有理数一样, 在实数范围内:
, 2可以看作分别是面积为5, 4的正方形的边长, 容易说明: 面积较大的正方形,它的边长也较大, 因此
同样, 因为5<9, 所以
不用计算器, 与2比较哪个大?与3比较呢?
新知探究
新知探究
例2: 在数轴上表示下列各点, 比较它们的大小,
并用 “ < ” 连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< < .
例3: 估计 位于 ( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
新知探究
例4: 比较下列各组数的大小.
解: (1)因为 12 < 42,
所以 < 4,
所以 -1< 3.
(2)因为 10 > 32 ,
所以
所以
(2)
课堂小结
实数
无理数: 无限不循环小数.
实数: 有理数和无理数统称为实数.
两种分类: ①根据实数的定义;
②根据实数的正负性.
实数与数轴上的点成一一对应关系.
课堂小测
1.下列说法正确的是( )
A.a 一定是正实数 B. 是有理数
C. 是有理数 D.数轴上任一点都对应一个有理数
B
2.有一个数值转换器, 原理如下, 当输 x=81时, 输出的y是 ( )
输入x
取算术平方根
是无理数
输出y
是有理数
A.9 B.3 C. D.±3
C
课堂小测
3.判断
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
课堂小测
4.把下列各数填入相应的括号内:
(1)有理数: {
(2)无理数: {
(3)整数: {
(4)负数: {
(5)分数: {
(6)实数: {
}
}
}
}
}
}
第六章
实数
七年级数学人教版·下册
6.3.1 实数的概念
授课人:XXXX
教学目标
1.正确理解实数的概念;(重点)
2.了解实数和数轴上的点一一对应, 能用数轴上的点
表示无理数.(难点)
有理数包括整数和分数, 如果将下列分数写成小数的形式, 你有什么发现?
整数能写成小数的形式吗?3可以看成是3.0吗?
它们都可以化成有限小数或无限循环小数的形式.
可以.
有理数都可化成有限小数或无限循环小数的形式.
反过来, 任何有限小数或无限循环小数也都是有理数.
新课导入
新课导入
我们学过的数是否都具有以上问题中数的特征?请举例说明.
不是.
它们都是无限不循环小数, 还是有理数吗?
知识归纳
无理数: 无限不循环小数.
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数, 如
1.01001000100001…
无理数的概念
新知探究
我们将有理数和无理数统称为实数, 仿照有理数的分类吗?据此你能给实数分类吗?
无理数:无限不循环小数
有理数:有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
实数的分类
新知探究
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
新知探究
无理数:
有理数:
正实数:
负实数:
例1: 将下列各数分别填入下列相应的括号内:
注意: 对每个数都要进行判断, 分类标准不同结果不同.
新知探究
思考1: 如图, 直径为1个单位长度的圆从原点沿数轴向右滚动一周, 圆上一点从原点到达A点, 则数轴上表示点A的数是多少
因为圆的周长为π, 无理数π可以用数轴上的点来表示.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
实数与数轴上的点
把两个边长为1的小正方形通过剪、拼, 得到一个大正方形, 大正方形的边长为 , 从而说明边长为1的小正方形的对角线为 .
新知探究
思考2: 你能在数轴上表示出 和 - 吗?
1
1
1
1
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来, 数轴上的每一点都表示一个实数.
实数和数轴上的点是一 一对应的.
新知探究
实数的大小比较
与有理数规定的大小一样, 数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零, 负数小于零, 正数大于负数;
2.两个正数, 绝对值大的数较大;
3.两个负数, 绝对值大的数反而小.
与有理数一样, 在实数范围内:
, 2可以看作分别是面积为5, 4的正方形的边长, 容易说明: 面积较大的正方形,它的边长也较大, 因此
同样, 因为5<9, 所以
不用计算器, 与2比较哪个大?与3比较呢?
新知探究
新知探究
例2: 在数轴上表示下列各点, 比较它们的大小,
并用 “ < ” 连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< < .
例3: 估计 位于 ( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
新知探究
例4: 比较下列各组数的大小.
解: (1)因为 12 < 42,
所以 < 4,
所以 -1< 3.
(2)因为 10 > 32 ,
所以
所以
(2)
课堂小结
实数
无理数: 无限不循环小数.
实数: 有理数和无理数统称为实数.
两种分类: ①根据实数的定义;
②根据实数的正负性.
实数与数轴上的点成一一对应关系.
课堂小测
1.下列说法正确的是( )
A.a 一定是正实数 B. 是有理数
C. 是有理数 D.数轴上任一点都对应一个有理数
B
2.有一个数值转换器, 原理如下, 当输 x=81时, 输出的y是 ( )
输入x
取算术平方根
是无理数
输出y
是有理数
A.9 B.3 C. D.±3
C
课堂小测
3.判断
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
课堂小测
4.把下列各数填入相应的括号内:
(1)有理数: {
(2)无理数: {
(3)整数: {
(4)负数: {
(5)分数: {
(6)实数: {
}
}
}
}
}
}
