2021-2022学年度人教版七年级数学下册课件 7.1.1 有序数对 (共22张PPT)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学下册课件 7.1.1 有序数对 (共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 14:29:40 | ||
图片预览




文档简介
(共22张PPT)
第七章
平面直角坐标系
七年级数学人教版·下册
7.1.1 有序数对
授课人:XXXX
教学目标
1.理解有序数对的概念;(重点)
2.理解有序实数对和点的一一对应, 根据事物的位置建立
直角坐标.(难点)
当发现一本书某页有一处印刷错误时, 你怎样告诉其他同学这一处的位置?
说明该页上 “ 第几行 ” 和 “ 第几个字 ” , 同学就可以快速找到错误的位置.
新课导入
新课导入
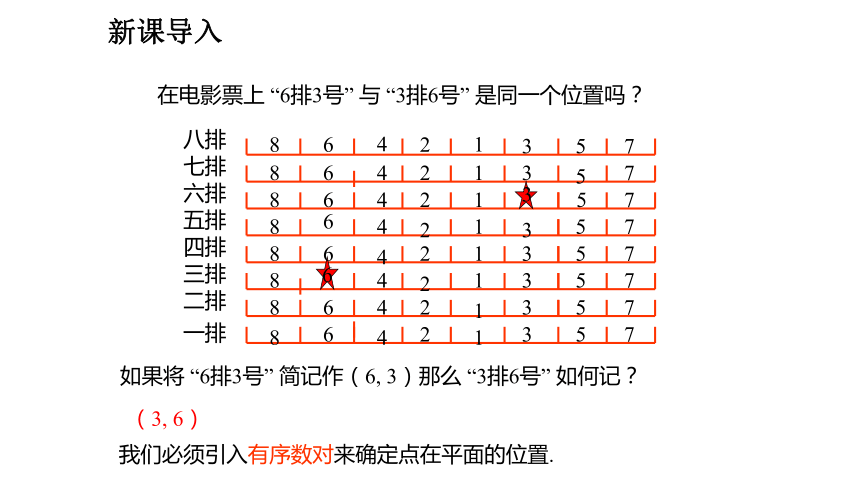
在电影票上 “6排3号” 与 “3排6号” 是同一个位置吗?
如果将 “6排3号” 简记作(6, 3)那么 “3排6号” 如何记?
一排
1
二排
三排
四排
五排
六排
七排
八排
1
1
1
1
1
1
1
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
6
6
6
6
6
6
6
7
7
7
7
7
7
7
8
8
8
8
8
8
8
8
6
7
2
(3, 6)
我们必须引入有序数对来确定点在平面的位置.
新知探究
1
2
3
4
5
6
讲台
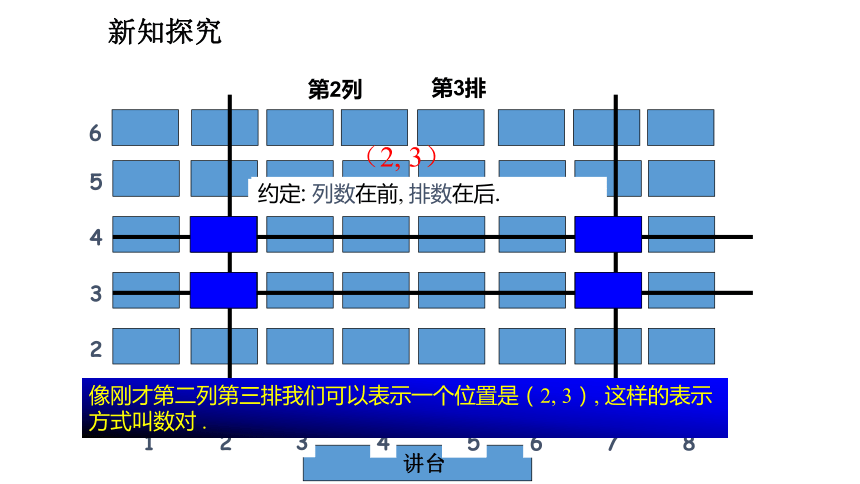
第2列
第3排
2
1
3
4
5
6
7
8
像刚才第二列第三排我们可以表示一个位置是(2, 3), 这样的表示方式叫数对 .
(2, 3)
( 列数, 排数)
约定: 列数在前, 排数在后.
新知探究
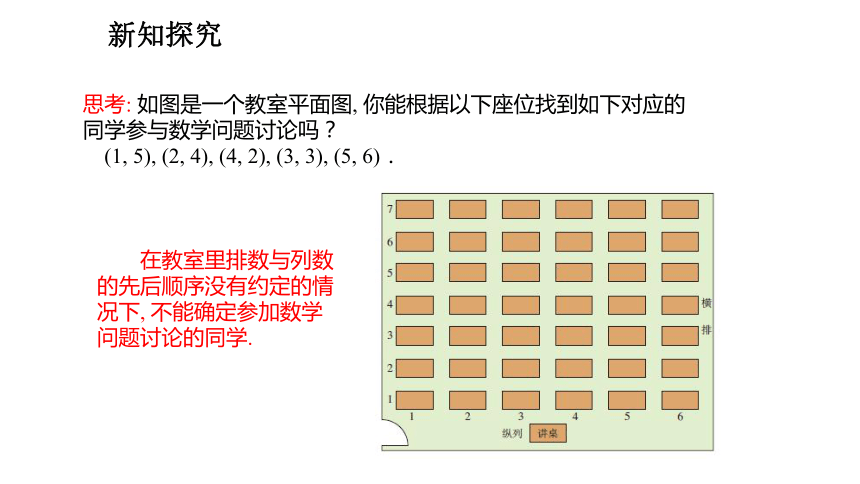
思考: 如图是一个教室平面图, 你能根据以下座位找到如下对应的同学参与数学问题讨论吗?
(1, 5), (2, 4), (4, 2), (3, 3), (5, 6).
在教室里排数与列数的先后顺序没有约定的情况下, 不能确定参加数学问题讨论的同学.
新知探究
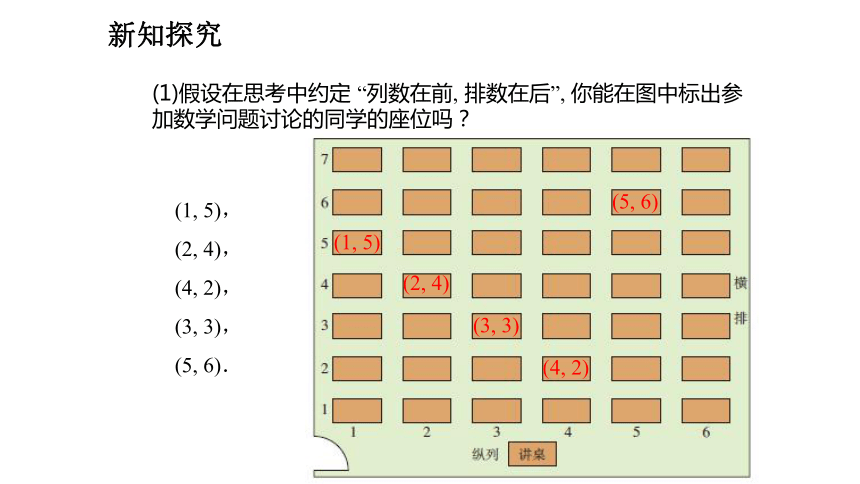
(1)假设在思考中约定 “列数在前, 排数在后”, 你能在图中标出参加数学问题讨论的同学的座位吗?
(1, 5)
(2, 4)
(4, 2)
(3, 3)
(5, 6)
(1, 5),
(2, 4),
(4, 2),
(3, 3),
(5, 6).
新知探究
(2)由上面可知, “第1列第3排” 简记为(1, 3)(约定列在前, 排在后), 那么
“第3列第5排” 能简记成什么?(6, 7)表示的含义是什么?
“第3列第5排” 记为(3, 5); (6,7)表示的含义是第6列第7排.
(3)同样约定 “列数在前, 排数在后” , (2, 4)和(4, 2)在同一个位置吗?
两者不在同一个位置. 因为(2, 4)表示第2列第4排, (4, 2)表示第4列第2排.
新知探究
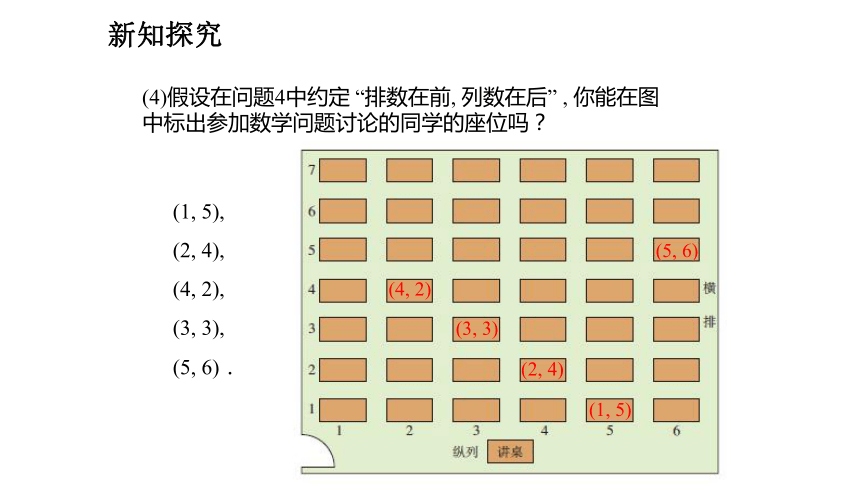
(4)假设在问题4中约定 “排数在前, 列数在后” , 你能在图中标出参加数学问题讨论的同学的座位吗?
(1, 5)
(4, 2)
(2, 4)
(3, 3)
(5, 6)
(1, 5),
(2, 4),
(4, 2),
(3, 3),
(5, 6).
知识归纳
我们把这种有顺序的两个数 a与b组成的数对, 叫做有序数对.
记做( a, b).
注意: (1)平面内确定一个位置需要两个数据, 数对是有顺序的.
(2)(a,b)与(b,a)不一样吗
新知探究
“怪兽吃豆豆” 是一种计算机游戏, 图中的●标志表示 “怪兽” 先后经过的几个位置, 如果用(1, 2)表示 “怪兽” 经过的第2个位置, 那么你能用同样的方式表示出图中 “怪兽” 经过的其他几个位置吗?
1
2
3
4
5
1
2
3
4
5
6
7
8
排
列
(3, 2)
(4, 3)
(3, 3)
(4, 5)
(5, 4)
(5, 5)
(7, 4)
(7, 3)
(8, 3)
(1, 1)
(1, 2)
新知探究
思考: 在地球上如何确定城市的位置?
在地球上有横线和竖线, 连接两极点的竖线叫经线, 垂直于经线的横线圈为纬线.
根据经纬线可以确定地球上任何一点的正确位置.
新知探究
北京: 东经116°
北纬40°
新知探究
5 可 明 喜 万 女
4 中 我 的 常 学
3 爱 数 天 唱 活
2 球 里 非 生 大
1 欢 孩 打 习 歌
A B C D E
区 域 划 分
若用C3表示 “天”, 请按下列顺序组成两句话:
(1) B4 A3 B3 E4
(2) B4 C2 D4 C5 A1 D3 E1
答案:
(1) 我爱数学
(2) 我非常喜欢唱歌
新知探究
如图: 若黑马的位置用(3, 7)表示, 请你用有序数对表示黑马可以走到的哪几个位置.
(1, 6)
(1, 8)
(2, 9)
(4, 9)
(5, 6)
新知探究
在下面的方格内用线段顺次连接(1, 3), (6, 7), (4, 3), (6, 4), (6, 2), (4, 3), (5, 1), (1, 3), 看组成什么图案?
8 7 6 5 4 3 2
1 2 3 4 5 6 7 8 9
排
列
.
.
.
.
.
.
.
.
课堂小结
有序数对
有顺序的两个数a与b组成的数对叫做有序数对, 记作(a, b).
(a, b)与(b, a)表示的是两个不同的位置.
可用有序数对表示实际问题, 用有序数对可绘成各种图案.
课堂小测
1.这是某班几个同学写出来的几个有序数对, 谁写对了?
A (5、9)
B (x, y)
E (b, 9)
C 4, 6
D (a b)
×
√
×
×
√
课堂小测
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
2.已知大门的位置, 用有序数对表示学校里的各个地点.
课堂小测
5 预 明 满 万 次
4 中 活 此 成 学
3 祝 英 天 ! 动
2 球 里 区 生 大
1 功 社 打 习 圆
A B C D E
3.如图, 方块中用(C, 3)表示 “天” 那么按下列要求排列会组成一句什么话, 把它读出来.
(A, 5 ) (A, 3) (C, 4 ) (E, 5 ) (B, 1) (C, 2) (B, 4)
(E, 3) (E, 1) (C, 5) (D, 4) (A, 1) (D, 3)
预
祝
此
次
社
区
活
动
圆
满
成
功
!
课堂小测
排
列
4.如果(1, 3)表示第1列第3排, 请用彩笔把以下位置的五角星涂上颜色.
(1, 6)
(2, 6)
(3, 5) (4, 4)
(5, 2)
(6, 2)
(7, 4)
第七章
平面直角坐标系
七年级数学人教版·下册
7.1.1 有序数对
授课人:XXXX
教学目标
1.理解有序数对的概念;(重点)
2.理解有序实数对和点的一一对应, 根据事物的位置建立
直角坐标.(难点)
当发现一本书某页有一处印刷错误时, 你怎样告诉其他同学这一处的位置?
说明该页上 “ 第几行 ” 和 “ 第几个字 ” , 同学就可以快速找到错误的位置.
新课导入
新课导入
在电影票上 “6排3号” 与 “3排6号” 是同一个位置吗?
如果将 “6排3号” 简记作(6, 3)那么 “3排6号” 如何记?
一排
1
二排
三排
四排
五排
六排
七排
八排
1
1
1
1
1
1
1
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
6
6
6
6
6
6
6
7
7
7
7
7
7
7
8
8
8
8
8
8
8
8
6
7
2
(3, 6)
我们必须引入有序数对来确定点在平面的位置.
新知探究
1
2
3
4
5
6
讲台
第2列
第3排
2
1
3
4
5
6
7
8
像刚才第二列第三排我们可以表示一个位置是(2, 3), 这样的表示方式叫数对 .
(2, 3)
( 列数, 排数)
约定: 列数在前, 排数在后.
新知探究
思考: 如图是一个教室平面图, 你能根据以下座位找到如下对应的同学参与数学问题讨论吗?
(1, 5), (2, 4), (4, 2), (3, 3), (5, 6).
在教室里排数与列数的先后顺序没有约定的情况下, 不能确定参加数学问题讨论的同学.
新知探究
(1)假设在思考中约定 “列数在前, 排数在后”, 你能在图中标出参加数学问题讨论的同学的座位吗?
(1, 5)
(2, 4)
(4, 2)
(3, 3)
(5, 6)
(1, 5),
(2, 4),
(4, 2),
(3, 3),
(5, 6).
新知探究
(2)由上面可知, “第1列第3排” 简记为(1, 3)(约定列在前, 排在后), 那么
“第3列第5排” 能简记成什么?(6, 7)表示的含义是什么?
“第3列第5排” 记为(3, 5); (6,7)表示的含义是第6列第7排.
(3)同样约定 “列数在前, 排数在后” , (2, 4)和(4, 2)在同一个位置吗?
两者不在同一个位置. 因为(2, 4)表示第2列第4排, (4, 2)表示第4列第2排.
新知探究
(4)假设在问题4中约定 “排数在前, 列数在后” , 你能在图中标出参加数学问题讨论的同学的座位吗?
(1, 5)
(4, 2)
(2, 4)
(3, 3)
(5, 6)
(1, 5),
(2, 4),
(4, 2),
(3, 3),
(5, 6).
知识归纳
我们把这种有顺序的两个数 a与b组成的数对, 叫做有序数对.
记做( a, b).
注意: (1)平面内确定一个位置需要两个数据, 数对是有顺序的.
(2)(a,b)与(b,a)不一样吗
新知探究
“怪兽吃豆豆” 是一种计算机游戏, 图中的●标志表示 “怪兽” 先后经过的几个位置, 如果用(1, 2)表示 “怪兽” 经过的第2个位置, 那么你能用同样的方式表示出图中 “怪兽” 经过的其他几个位置吗?
1
2
3
4
5
1
2
3
4
5
6
7
8
排
列
(3, 2)
(4, 3)
(3, 3)
(4, 5)
(5, 4)
(5, 5)
(7, 4)
(7, 3)
(8, 3)
(1, 1)
(1, 2)
新知探究
思考: 在地球上如何确定城市的位置?
在地球上有横线和竖线, 连接两极点的竖线叫经线, 垂直于经线的横线圈为纬线.
根据经纬线可以确定地球上任何一点的正确位置.
新知探究
北京: 东经116°
北纬40°
新知探究
5 可 明 喜 万 女
4 中 我 的 常 学
3 爱 数 天 唱 活
2 球 里 非 生 大
1 欢 孩 打 习 歌
A B C D E
区 域 划 分
若用C3表示 “天”, 请按下列顺序组成两句话:
(1) B4 A3 B3 E4
(2) B4 C2 D4 C5 A1 D3 E1
答案:
(1) 我爱数学
(2) 我非常喜欢唱歌
新知探究
如图: 若黑马的位置用(3, 7)表示, 请你用有序数对表示黑马可以走到的哪几个位置.
(1, 6)
(1, 8)
(2, 9)
(4, 9)
(5, 6)
新知探究
在下面的方格内用线段顺次连接(1, 3), (6, 7), (4, 3), (6, 4), (6, 2), (4, 3), (5, 1), (1, 3), 看组成什么图案?
8 7 6 5 4 3 2
1 2 3 4 5 6 7 8 9
排
列
.
.
.
.
.
.
.
.
课堂小结
有序数对
有顺序的两个数a与b组成的数对叫做有序数对, 记作(a, b).
(a, b)与(b, a)表示的是两个不同的位置.
可用有序数对表示实际问题, 用有序数对可绘成各种图案.
课堂小测
1.这是某班几个同学写出来的几个有序数对, 谁写对了?
A (5、9)
B (x, y)
E (b, 9)
C 4, 6
D (a b)
×
√
×
×
√
课堂小测
8
1
2
3
4
5
6
7
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
大门
食堂
宿舍楼
宣传橱窗
实验楼
教学楼
运动场
办公楼
(9,6)
(8,5)
(3,7)
(6,8)
(7,4)
(2,2)
(3,3)
(5,2)
2.已知大门的位置, 用有序数对表示学校里的各个地点.
课堂小测
5 预 明 满 万 次
4 中 活 此 成 学
3 祝 英 天 ! 动
2 球 里 区 生 大
1 功 社 打 习 圆
A B C D E
3.如图, 方块中用(C, 3)表示 “天” 那么按下列要求排列会组成一句什么话, 把它读出来.
(A, 5 ) (A, 3) (C, 4 ) (E, 5 ) (B, 1) (C, 2) (B, 4)
(E, 3) (E, 1) (C, 5) (D, 4) (A, 1) (D, 3)
预
祝
此
次
社
区
活
动
圆
满
成
功
!
课堂小测
排
列
4.如果(1, 3)表示第1列第3排, 请用彩笔把以下位置的五角星涂上颜色.
(1, 6)
(2, 6)
(3, 5) (4, 4)
(5, 2)
(6, 2)
(7, 4)
